对2017年全国卷Ⅰ立体几何解答题的探究

●

(兴宁市第一中学，广东 兴宁 514500)

对2017年全国卷Ⅰ立体几何解答题的探究

●蓝云波

(兴宁市第一中学，广东 兴宁 514500)

文章以2017年全国数学高考卷Ⅰ立体几何解答题为研究内容，从试题欣赏、解法探究、教学反思3个方面进行了深入地剖析，从而为以后的数学高考备考提供一定的借鉴作用.

高考试题;立体几何;一题多解;教学反思

自2016年起，广东省数学高考结束了多年的自主命题模式而加入全国卷.相比广东卷，全国卷的试题难度相对较高，因此对广东考生而言，普遍感觉难度较大.如何适应新高考形势是教师必须要认真面对的课题.研究全国卷高考试题是教学研究的重要途径与手段，通过研究真题，可获知全国卷的命题要求、方向、风格，从而制定切实可行的高效课堂教学方法.笔者对2017年全国卷Ⅰ立体几何试题进行分析，谈谈该题的试题分析、解法探究与教学反思，以期对新一年的数学高考备考有一定的借鉴作用.

1 试题赏析

例1如图1，在四棱锥P-ABCD中，AB∥CD且∠BAP=∠CDP=90°.

图1

1)证明：平面PAB⊥平面PAD.

2) (理)若PA=PD=AB=DC，∠APD=90°，求二面角A-PB-C的余弦值；

(2017年全国数学高考卷Ⅰ第18题)

例1具有以下的特色：

首先，例1中文理科立体几何解答题是姊妹题，较好地体现了文理科考生的实际与差异，很好地体现了新课标立体几何内容对文理科考生的不同要求.例1面目温和、表述简洁、设问层层递进，易于入手，难度适中，是一道能让考生迅速进入状态的平和试题.

其次，考查了立体几何中的主干知识与基本思想方法，注重学生空间想象能力的考查.试题以锥体为载体，考查了平面与平面垂直的判定、二面角(理科)的求法、几何体的体积与侧面积(文科)的求法等核心考点，体现了高考重点知识重点考查的原则.对学生空间想象能力的考查相对深入，是一道能较好甄别出学生知识能力水平和数学素养的好题，并具有一定的区分度.

2 解法探究

在近几年全国卷Ⅰ的高考试题中，立体几何题型比较稳定[1].立体几何常常以锥体或柱体为载体，理科命题呈现一题两法(传统法与空间向量法)的格局.一直以来，立体几何解答题让广大理科学生又喜又忧：为之而喜是因为只要能建立空间直角坐标系，基本上可以处理立体几何绝大多数的问题；为之而忧就是对于不规则图形而言，建系的难度较大，问题不能得到很好地解决，而运用传统方法，要作多条辅助线，学生较为畏惧.

对文科考生而言，除了要重点掌握好平行与垂直关系的证明外，体积问题是文科考生必须面对的一大难点.纵观近几年全国卷Ⅰ文科立体几何试题，第2)小题往往是有关几何体体积的综合问题，对空间想象能力的考查比较深入.对于体积问题，常见的解题方法有作高法、等体积法、割补(间接)法等.

1)证明由∠BAP=∠CDP=90°，得

AB⊥PA,DC⊥PD.

因为AB∥CD，所以

AB⊥PD，

而PD∩PA=P，PD,PA⊂平面PAD,从而AB⊥平面PAD.又因为AB⊂平面PAB，所以平面PAB⊥平面PAD.

评注文理考题第1)小题相同，是姊妹题的常见命题方式，此小题考查了立体几何垂直关系中的面面垂直判定，考生常犯的错误是对判定定理不熟悉，在没有证明线面垂直的情况下就得出结果.笔者在教学过程中发现，学生在立体几何学习中的一个突出问题是对立体几何的相关概念、公理、定理等知识模糊不清，理解不到位，常常出现不根据概念、公理、定理进行论证或没有正确使用概念、公理、定理论证的情况，这是教学中教师要重点解决的一大“顽疾”.

下面先对例1理科第2)小题进行分析.

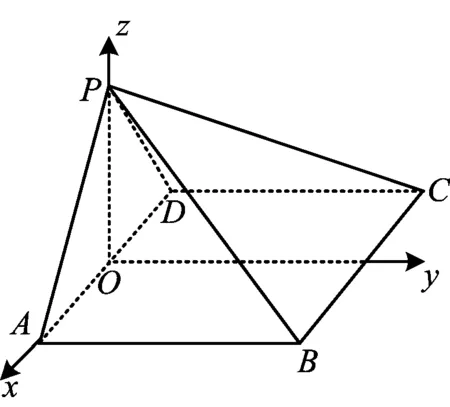
图2

2)(理)解法1在平面PAD内作PO⊥AD，垂足为O.由第1)小题知，AB⊥平面PAD，PO⊂平面PAD，从而AB⊥PO.又AD∩AB=A，于是PO⊥平面ABCD.

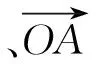
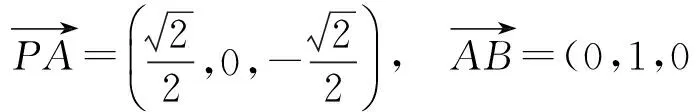
设n=(x1,y1,z1)是平面PCB的一个法向量，则

即

设m=(x2,y2,z2)是平面PAB的一个法向量，则

即

令x2=1，得m=(1,0,1),则

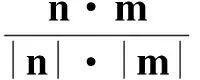
评注对理科考生而言，二面角是立体几何学习的一大难点.解法1使用的是学生比较喜欢的空间向量坐标法，通过求解两个法向量，从而实现问题的求解.“二面角是锐角还是钝角”的判断是学生的一大盲点，教学中可结合图形与法向量的方向进行判断.另一个突出的问题是法向量如何准确求解.通过统计发现，能准确计算出法向量的学生并不多.因此，这也是教学中必须解决的一大难题.

对于空间向量方法，可能很多教师都着重突出空间向量坐标法，实际上，空间向量基底法也是解题的一大利器.

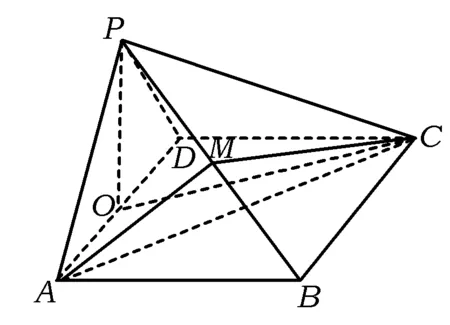
图3

解法2如图3，在平面PAD内作PO⊥AD，垂足为O.由第1)小题知，AB⊥平面PAD，而PO⊂平面PAD，于是AB⊥PO.又AB∩AD=A，从而PO⊥平面ABCD.设AB=x，则由已知可得

从而

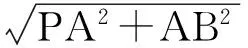
在Rt△PAB中，

取PB的中点M，由PA=AB，知AM⊥PB，又PC=BC，从而CM⊥PB，于是∠AMC是二面角A-PB-C的平面角，故

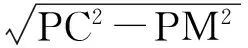
在△AMC中，由余弦定理得

评注本题使用了二面角求法当中的定义法，求解的关键是对图形中边角关系的细致观察以及对基本概念的理解是否到位.对于传统解法，大部分学生都比较畏惧，因为要作多条辅助线.在教学中，不少教师也着重于空间向量坐标法的教学，以为见效较快，但对于某些难于建系的问题，空间向量坐标法的弱点也凸显无疑.因此，对传统法的教学不宜急功近利，应做到细水长流，讲清基本原理和方法.

图4

解法3如图4，过点P作PQ∥DC且PQ=DC，联结QB，QC，则四边形PQCD为平行四边形.因为AB∥CD，且AB=CD，所以PQ∥AB，且PQ=AB，即四边形PQBA为平行四边形.

取PB的中点M，联结QM，并延长QM交PA于点N，由QP=QB，知QN⊥PB.因为AB⊥平面PAD，PD⊂平面PAD，所以AB⊥PD，又QC∥PD，于是QC⊥AB.因为PD⊥PA，QC∥PD，所以QC⊥PA，而PA∩AB=A，于是QC⊥平面PQBA，而PB⊂平面PQBA，故QC⊥PB.又因为PB⊥QN，而QC∩QN=Q，所以PB⊥平面QMC，又MC⊂平面QMC，知PB⊥MC，从而∠NMC为二面角A-PB-C的平面角，且∠QMC为其补角.设AB=x，则由已知可得

从而cos∠NMC= cos(π-∠QMC)=-cos∠QMC=

评注对于钝二面角问题，割补法也是一大利器，如解法3，只要利用割补法，作出图形并进行充分论证，计算极为简洁，不失为一种好的解法,对学生空间想象能力的培养具有重要的作用.

下面我们来看例1文科第2)小题的求解.

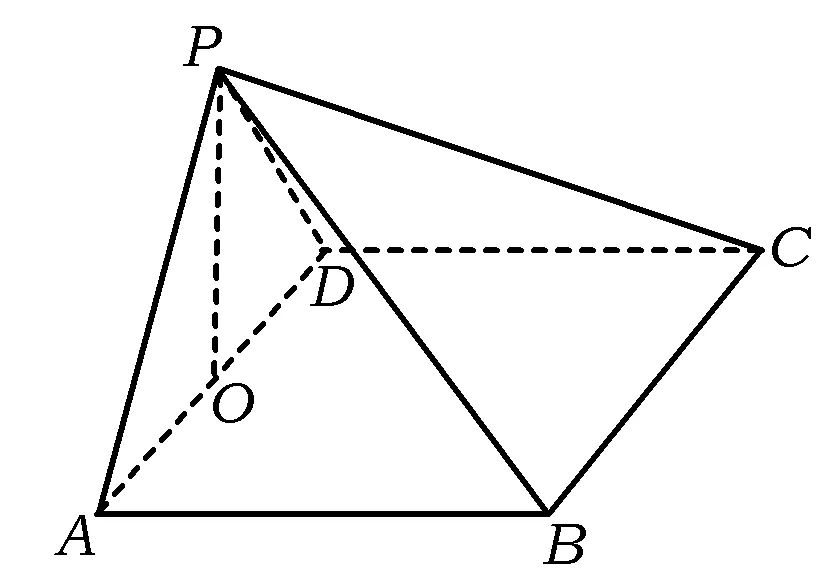
图5

2)(文)解如图5，在平面PAD内作PO⊥AD，垂足为O.由第1)小题知，AB⊥平面PAD，而PO⊂平面PAD，于是AB⊥PO，又AB∩AD=A，从而PO⊥平面ABCD.设AB=x，则由已知可得

故四棱锥P-ABCD的体积为

评注对于文科考生来说，立体几何中平行与垂直关系的证明并不是难度很大的问题，在教学中，重点要解决的问题是立体几何证明的条理性与书写的严谨性.而体积问题是学生学习的一大难点，本题中由于几何体的高较容易作出，于是使用了作高法，实现问题的求解；对于几何体的高较难作出的问题，则可考虑等体积法与割补法，如下面的3道试题.

1)证明：直线GM∥平面DEF；

2)求三棱锥M-DEF的体积.

(2017年河北省石家庄市二模文科试题第18题)

图6 图7

例3如图7，已知在三棱柱ABC-A1B1C1中，AA1=2AB=2AC=2，∠BAC=90°，∠BAA1=120°.

1)证明：AB⊥平面AB1C；

2)求四棱锥B1-AA1C1C的体积.

(2017年湖北省四校第一次数学联考文科试题第18题)

图8

例4如图8，正方形ABCD所在平面与⊙O所在平面相交于CD，线段CD为⊙O的弦，AE垂直于⊙O所在平面，垂足E是⊙O上异于C,D的点，AE=3，⊙O的直径CE为9.

1)求证：平面ABE⊥平面ADE；

2)求五面体ABCDE的体积.

(2017年安徽省安师大附中、马鞍山二中高三阶段性测试数学文科试题第19题)

以上3道题第1)小题都考查了空间中的平行与垂直关系的证明问题，难度不大.对于第2)小题的体积问题，例2由于所要求解的是几何体的体积，难于直接作出几何体的高，结合题意，可选用等体积法VM-DEF=VG-DEF=VF-DEG进行求解，考查了化归与转化思想，对逻辑思维能力有一定的要求；例3直接求解几何体的体积较为困难，但通过观察，可先求出三棱锥B1-ABC的体积，从而间接求出所要求的几何体的体积；例4通过把所要求的几何体分割成两个简单的几何体，利用VABCDE=VB-CDE+VB-ADE化难为易，是求解几何体的一种常见策略，应引起足够的重视.

3 教学反思与建议

通过对例1的分析，笔者认为，在数学教学中，教师应做到：

1)要重视教材，重视学生的基本功训练.要注重数学的基本概念、原理、方法的传授，特别是在高三的备考过程中，教师切不可认为这些基础知识只要简单带过即可，切不可错误地认为只有通过题海战术才能提高学生的解题能力.事实上，数学基本知识与基本技能对学生的长远发展具有举足轻重的作用，是数学本质的体现，对学生数学素养的提高具有不可估量的作用.

2)要注重培养学生一题多解、一解多题、一题多变等变式能力的训练.这对学生思维能力的提高具有不可替代的作用，能发散学生思维，防止思维定势，对学生以后的学习大有裨益[2].同时，教师要注重典型例题的分析、变式训练.

3)要重视学生数学思想的培养，在教学中要重视学生数学思想方法的发生、生成、内化、升华过程.如立体几何中空间想象能力的培养，不可急功近利，特别是理科立体几何的教学，空间向量方法与传统方法都不可偏废，两手都要硬.而空间角的计算，综合法与向量法各有千秋，在复习时应两种方法并重[3].文科立体几何教学要培养多视角解决体积问题的能力.数学思想与方法是数学基本功中的“内力”，并非一朝一夕能改变，教师要意识到这是细水长流的过程，不能急功近利，从而让学生在长期接触与体会中得到升华.

4)应善于学习，努力提高自己的业务能力，要能站在较高的角度看待和审视问题.要适应新一轮课改“培养学生立德树人的目标，提高学生核心素养”的要求.通过学习，不断提高自身的基本素养与技能,这样才能识别出隐藏在试题背后的核心数学思想与素养,并发掘其中有价值的东西传授给学生，做到“会当凌绝顶，一览众山小”.

[1] 杜红全.追踪考题 晒晒考点——“立体几何”高考考点题型归类解析[J].中学教研(数学)，2017(2)：40-44.

[2] 蓝云波.对2015年湖北高考立体几何试题的探究[J].中学数学：高中版，2015(11)：39-41.

[3] 张晓东.立体几何的复习策略[J].中学教研(数学)，2015(2)：20-24.

2017-10-16

广东省梅州市第九届教育教学科研立项课题(MZ0901-XNS202)

蓝云波(1981-)，男，广东兴宁人，中学一级教师.研究方向：数学教育.

O123.2

A

1003-6407(2017)12-31-04