在对话中生成 在探究中出彩

●

(南京市第二十九中学,江苏 南京 210036)

在对话中生成在探究中出彩

●郭建华

(南京市第二十九中学,江苏 南京 210036)

文章通过师生交流分析学生的错题，在教师的引导下通过师生对话，逐渐扫清学生所存在的知识盲点，从而培养学生求解向量问题的意识，以此提升课堂效率，把数学核心素养落实在课堂上.

师生对话；交流互动；探究合作

“问题”是探究的起点，数学课堂教学中学生问题的提出，需要经过教师主导下的选择、定向或优化而最终形成学习和探究的任务.那么，如何激发学生的问题意识，如何以问题为核心规划学习内容，如何让数学课堂变得精彩呢？通过习题的讲评，如何让数学习题课真正变成在教师引导下进行再发现、再创造的学习活动呢？笔者认为：教师应该以学生为主体，通过师生和生生交流对话，为学生创造更多的思考时间和探究机会，鼓励更多的学生参与课堂，真正让学生“动”起来，让课堂“活”起来，不断将数学核心素养落在实处.特别是高三的数学教学，更是要追求在有限的复习时间内让学生实现深度学习和高效课堂的目标.

1 原题回放

图1

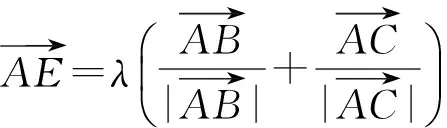
1)求BC的长；

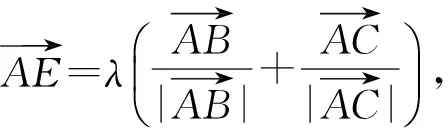
这是笔者高三一轮复习时遇到的一道阶段检测试题，本题以解三角形为背景，以向量为载体，蕴含了数形结合、转化与化归、函数与方程等数学思想.第1)小题主要考查正余弦定理的应用，第2)小题主要考查向量的基本知识和运算以及角平分线的性质.本题实现了对基础知识、基本技能和基本数学思想的考查，能较好地甄别学生的思维水平和提升学生的数学核心素养.本题的命题特色：背景平和，知识交汇，设计简洁，表达清晰，构思新颖.

2 考情分析

3 课堂实录

3.1 对话交流，探究解题策略

师：通过试卷的批改，主要问题在第2)小题，同学们所面临的最大障碍是什么？

生1：根据平行四边形法则，易得AE是∠BAC的平分线.

众生(恍然大悟)：原来是这样的呀！

设计意图通过了解学生急需要解决的困惑和痛处，将问题进行分解和设计，帮助学生回顾、复习、巩固向量的相关知识，加强对单位向量、加法法则等知识的掌握和理解，为后面的解题作好铺垫.

师：接下来如何求λ的值？

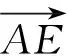
即

从而

即

师：请大家回到三角形中思考问题，不要孤立地去看这个问题.

教师巡视，观察学生的做法.3分钟后，部分学生跃跃欲试.

S△ABC=S△ABE+S△ACE,

学生们纷纷点头表示赞同.

生4：“等面积法”虽好，但不太容易想到.

设计意图在教师的引导下，“从整体上出发，在细微处入手”，给学生时间，鼓励学生动脑思考，从而唤醒学生的思维，找到解题的突破口.

师：大家还有什么想法？能分享一下吗?

生4：老师，我们以前做过几道向量题都是用“坐标法”，这道题也可以的.

教师投影生4的解题过程：

图2

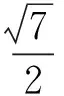
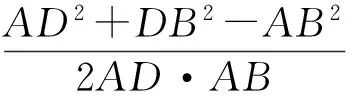
从而

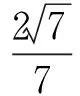
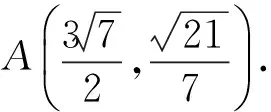
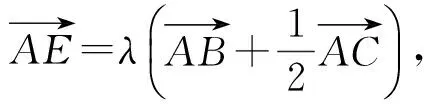
于是

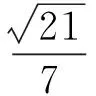
师：很好，只要找到适合自己的方法，并努力坚持，一定会成功的.“坐标法”也是处理与图形有关的向量问题的基本方法，那么使用“坐标法”的优越性在哪里？

生(众)：将几何问题转化为代数运算问题.

师：既然大家都熟悉这种方法，为什么考试的时候没有选择它呢？

生5：不是等边三角形、等腰三角形、直角三角形等对称图形或特殊图形，坐标系不好建.

生6：坐标点A不容易求.

……

生7：在△ABD中，经计算发现AB⊥AD，因此我也选择“坐标法”求解.

教师投影生7的解题过程：

图3

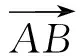
又点B，D，E共线，从而kBD=kBE，即

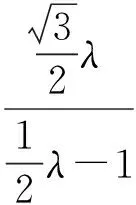
设计意图坐标法是解决向量问题的常用方法，通过解题训练，学生逐步具备这种意识.建立不同的坐标系将会带来不同的解题效果，因此，建立适当的坐标系是解题的关键，准确求出关键点的坐标是解题的重点．

师：通过创造条件建坐标系求解，生7的运算要优于生4.还有其他想法吗？

生8：受生7的启发，也可以利用点B，C，E共线、利用共线向量定理求解.

师：大家熟悉该定理吗？

教师留给学生时间回顾并阅读课本，学习共线向量定理，然后让学生回答.

生9：已知向量a，b，如果有一个实数λ，使b=λa(其中a≠0)，那么b与a是共线向量；反之，如果b与a是共线向量，那么有且只有一个λ，使b=λa.

师：如何使用该定理呢？

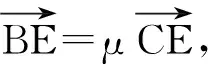
师：如何选择基底？

(λ-1)e1+λe2=μλe1+μ(λ-2)e2，

从而

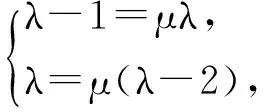
师：生8的数学功底不浅呐！运算简捷，解题方法明显得到优化.

教室内发出一阵赞叹声，为生8的做法喝彩.

设计意图在教师的引导、指导和帮助下，学生认真阅读课本，学会选择解题方法的依据，比如定义、定理、公式及常用的结论等.比如该解法从共线向量定理着手，选择恰当的基底，从而使问题破解.

生11(迫不及待地想和大家分享)：老师，我通过作图，利用平面几何知识也可以求λ.

教师投影生11的做法：

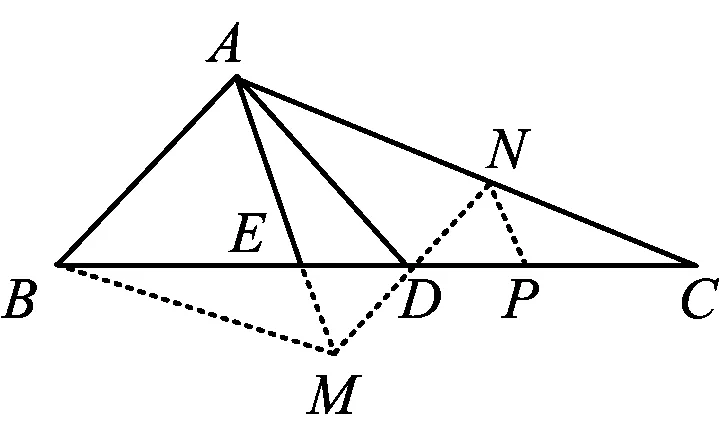
图4

如图4，取AC的中点N，联结ND并延长，使得ND=DM.因为D为BC的中点，所以

从而

AB=NM，

且AB∥NM.又AB=MN=1，从而四边形ABMN为菱形.由

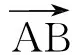
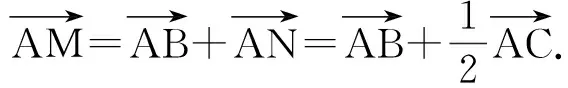
取EC的中点P，从而

又DM=DN，易得△DEM≌△DPN，于是

即

故

设计意图尊重学生的想法，尊重学生的话语权，通过作辅助线，由线段的位置关系凸显其数量关系，实现转化的目的.

师：看来大家对这道题的想法还是蛮多的，收获应该不少吧，还有其他想法吗？

师：哦，又有新的突破啦，大家熟悉三角形内角平分线定理吗？

大部分学生摇摇头表示已经忘记了，只有个别学生还能记起来，教师认为有必要复习该定理.

师：请大家回顾课本上哪个章节有出现过这个定理？

生13(很兴奋)：出现在《数学(必修5)》的解三角形中.

师：请大家翻开书重新认识和学习该定理.

几分钟后，教师投影生13的解题过程：

由三角形内角平分线定理，得

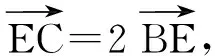
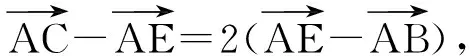
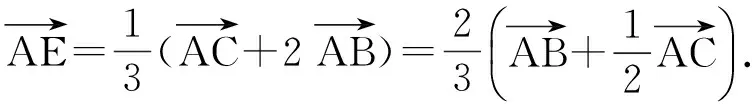
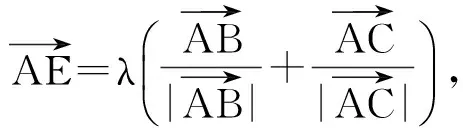
师：生13的解答过程既简捷又巧妙，不愧是一种好的方法.

教师话音刚落，教室里又响起一片掌声.

设计意图习题课教学需要教师的精心设计，整合上课素材，给学生思考的时间和动手操作的机会，指导学生阅读课本，让学生学会从课本中选择和提取解决问题的知识和方法.

3.2 编制题组，促进深化理解

学生对这道题的想法还是蛮多的，好像还意犹未尽，于是想借此机会拓展一下大家的思维.由于角平分线与三角形的内心有关，那么三角形的外心、重心与三角形的哪些因素相关呢？在教师的指导下，对这道题进行了改编，发挥其以点带面的功能，提高高三的复习效率.

师：请大家也来做一回命题专家，能否利用三角形的“内心”编制一道相似的题目？

师：很好，有想法还是值得赞扬的，说明对角平分线真正理解啦！

班里最爱思考问题的两位数学达人在讨论，刚好被教师听到：除了三角形的内心，能否利用三角形的重心命题呢？

师：很好，两位同学如果想好了可以和大家分享一下.

大家把问题都指向了三角形的重心，开始分组讨论，并将自己的想法记录下来，不断地尝试和修正……

生15：可以在生14的基础上再作一下改编:已知△ABC，点P满足

当λ∈[0,+∞)时,动点P的轨迹一定过△ABC的______(重心、内心、外心、垂心).

师：你是怎么想到的？

师：很好，同学们能否考虑用垂心来命题？同桌之间可以合作完成.

学生们开始思考，画图分析，不一会有了答案.

生16：已知△ABC，点P满足

当λ∈[0,+∞)时,动点P的轨迹一定过△ABC的______(重心、内心、外心、垂心).

师：很好，对分母的形式作一下改变，将给我们带来全新的视角，你能给大家说说你是怎么想到的吗？

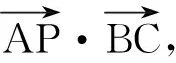
生(众)：哦，是这样的，我怎么没想到呢？

学生们恍然大悟，明白了编制试题不是一件容易的事情，同时对生16表示赞赏.

教师投影生16的解答过程：

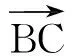
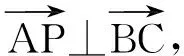
于是点P是边BC高线上一点，动点P的轨迹一定过△ABC的垂心.

设计意图通过题目各种形式的改编，比如变换问题的条件和结论、问题的形式等，培养学生的发散思维，促进学生的深度思考.在探究中只有解决问题的主要矛盾才能理解问题的本质，避免思维的狭隘性，这样才能真正促进学生的深度学习.

4 教学思考

高三数学习题课，教师不能只追求课堂“容量”，而应重视“质量”，用教师的智慧打造高效课堂.在教师的引导下调动学生的学习积极性，让学生主动参与思考，积极参与交流，让学生的思维“动”起来，这样的数学习题课才能真正有效和高效.学生是学习的主体，也是教学材料的实践者，通过培养学生的问题意识，让学生发现问题、提出问题，这样学生才会有“真思考”,才会用数学的方式思维，真正将数学核心素养落实在课堂上.

同时教师也要为学生创造和谐融洽的课堂氛围，让所有学生的思维动起来，实现师生互动、生生互动，建立师生共同发展的教学关系，使数学课堂成为师生的“学习共同体”.教师更要敢于放手课堂，追求一种“慢”教学，在教学过程中不断设置有利于激发学习潜能、锻炼学生思维的问题和情境，不断为学生创造探究的机会，提供思维的空间和时间.只有在课堂上选择适当的时机“慢”下来，学生才会有时间体会和感悟，才会理解问题的本质和掌握思维方法；才能让学生感受到习题课不是枯燥无味的，鼓励他们参与探究，尊重他们的话语权，通过交流暴露学生的思维，让不同层次的学生在课堂上都有收获，这样才能让课堂出彩.

2017-10-10

南京市教育科学“十三五”规划2016年度立项课题(L/2016/076)；江苏省教育科学“十三五”规划2016年度“教师发展研究专项”课题(J-c/2016/12)

郭建华(1982-)，男，安徽宿州人，中学一级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)12-18-05