微型探究揭本质 深度学习促素养
——一节习题研究课的教学活动及课后调研和思考
●
(仪征中学,江苏 仪征 211400)
微型探究揭本质深度学习促素养
——一节习题研究课的教学活动及课后调研和思考
●花奎
(仪征中学,江苏 仪征 211400)
如何提升习题研究课的有效性?可以通过探究错因,寻求正解;反思观察,优化方法;无疑生疑,揭示本质;总结应用,形成经验等教学流程进行教学.通过课后调研发现开展微型探究应做到以下几点:基于学生基础,把学生的思维作为解题教学的起点;基于对话交流,利用元认知提问驱动学生学习的动机;基于质疑反思,通过微型探究揭示数学本质.这样做能够促进学生深度学习,提升学生的思维层次和数学素养.
习题课;微型探究;深度学习;素养
习题是数学知识的载体,是数学思想方法的生长点,蕴涵着巨大的教育潜能.特别是在数学高考总复习中,习题研究课更为常见,如何提升习题研究课的有效性,一直是笔者思考的问题.近日,在江苏省扬州市领雁工程培养对象汇报课展示活动中,笔者听了一节高三习题研究课,是对一道习题的纠错探究教学,给笔者留下了深刻的印象.
1 教学片段实录
1.1 探究错因,寻求正解
题目设函数f(x)=ax3-3x+2(其中a∈R),若对于任意的x∈[-2,2]都有f(x)≥0成立,则实数a=______.
师:这是近日数学测试卷中的一道填空题,同学们的正确率不高,只有50%.这节课,我们就来研究这道题,希望有所收获.
教师投影生1的解题思路:
由题意知f′(x)=3ax2-3,令f′(x)=0得
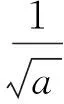

师:这部分的解答过程有问题吗?如何纠正?大家讨论一下.


(教师给学生6分钟左右的思考时间.)
生3(解法1):我认为应当分类讨论.
1)当a≤0时,f′(x)<0,此时f(x)在[-2,2]上单调递减,从而
f(x)min=f(2)=8a-4≥0,

2)当a>0时,令f′(x)=0,得
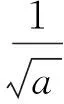
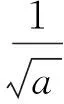
f(x)min=f(2)=8a-4≥0,

因此要使f(x)≥0在[-2,2]上恒成立,则
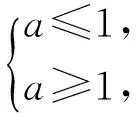
综上所述,a=1.
师:太好了!生3的解法将不等式f(x)≥0恒成立问题转化为最值问题,即f(x)min≥0,然后通过分类讨论来求f(x)min.分类讨论要求我们具备清晰的思维,逐一解决.大家再想想看,除了直接研究函数f(x)的最小值这种解题思路,不等式f(x)≥0恒成立问题还可以用什么方法来解决?
生4:参变量分离.
教师展示生4的解法:
f(x)≥0可化为ax3≥3x-2,即
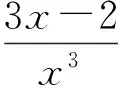
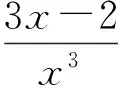

从而g(x)在(-2,1)上单调递增,在(1,2)上单调递减,于是
g(x)max=g(1)=1,
故a≥1.
师:大家思考一下,生4的做法有错吗?错在哪里呢?
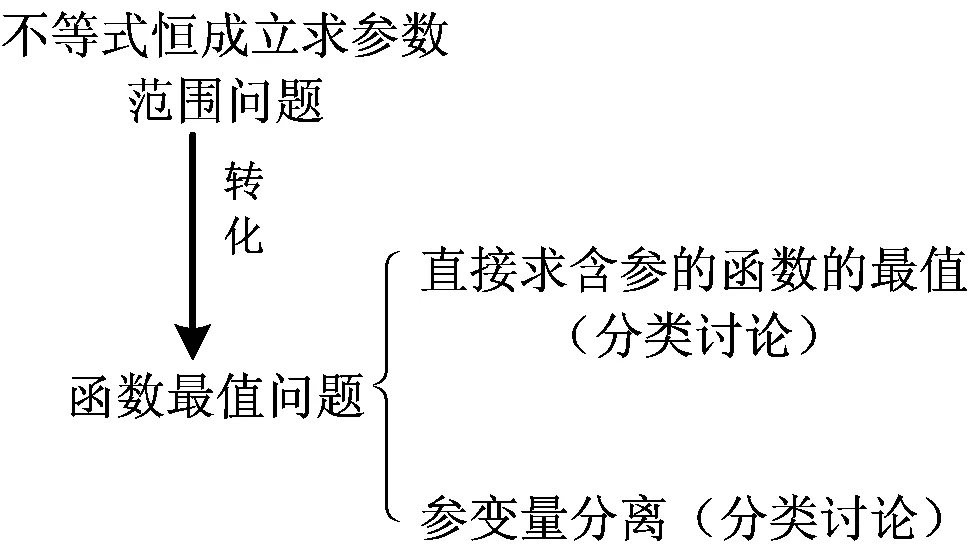
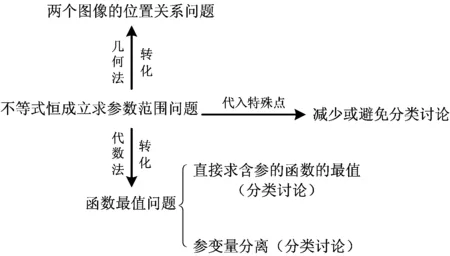
生4:老师,我知道错在哪里了!我没讨论:因为x∈[-2,2],需分x=0,0 师:生4自我反思和自我批评的精神值得我们学习!为什么要分类讨论呢? 生4:不等式ax3≥3x-2两边同除以x3,要考虑不等号的方向是否改变,即要考虑x3的正负性,而x的正负性不确定,因此要对x进行讨论. 师:说得很好,那么你能说说完整的解法吗? 生4(解法2):f(x)≥0恒成立,可化为ax3≥3x-2恒成立. 从而g(x)在(0,1)上单调递增,在(1,2)上单调递减,于是 g(x)max=g(1)=1, 故a≥1. 从而g(x)在[-2,0)上单调递增,于是 g(x)min=g(-2)=1, 故a≤1. 综上所述,a=1. 师:有问题吗? (生4疑惑地表示没有.) 生5:少讨论了x=0的情况,应添加第3种情况,即“3)当x=0时,不论a取何值,f(x)≥0恒成立”. 师:很好!分类讨论是一种常见的数学思想方法,要做到不重复不遗漏,这需要我们顽强的毅力和清晰的思维.现在,大家再回头思考一下这两种方法,是怎么想到分类讨论的?又是怎样讨论的?讨论的依据是什么? (教师给大家5分钟左右的题后反思总结.) 通过学生展示补充,形成以下认知网络: 图1 师:分类讨论是一种重要的数学思想方法,我们应当掌握.如此复杂的分类讨论,一不小心就会出错.那么,有没有其他方法来减少讨论,甚至避免分类讨论呢? (一石激起千层浪,众生顿时叽叽喳喳地讨论起来.) 生6:代入两个端点值,可以缩小a的范围? 师:哦,这是你们不会做时经常用的绝招,你继续说说看. (全班学生大笑.) 生6:f(x)≥0对x∈[-2,2]恒成立,则当x=±2时,f(x)≥0成立,即 生(众):只有一种! (学生们异口同声,惊叹这种方法的精彩!) 师:好!请尝试书写完整的解题过程. 生7:因为f(x)≥0对x∈[-2,2]恒成立,所以 令f′(x)=3ax2-3=0,得 要使f(x)≥0在[-2,2]恒成立,则 师:通过该方法的学习,以后解题时我们可以利用“特殊值效应”(即恒成立的必要条件)将参数的范围缩小,以减少分类讨论. 生8(迫不急待):老师,我的方法更简单! 师:你说说看!同学们也来听听,看有何新发现? (生8话音刚落,雷鸣般的掌声响了起来……) 师(示意大家安静):生8的做法太巧妙了,通过取特殊值夹逼出参数a的值.同学们做完这道题后有没有什么困惑? 在学生以为大功告成的时候,笔者又抛出一个新的问题,于无疑处生疑.学生们七嘴八舌,最后综合提出两个困惑:1)生8的做法很巧,特别是取x=1,夹逼出参数a的值,这是偶然还是必然呢?2)不等式恒成立问题一般都是求参数的范围,而不是求参数的值,为什么这里的参数a是一个具体值?学生们小声地交流着意见,但还是说不出所以然. 生9(过了一会儿):能否从图像的角度去看呢? 师:生9提出了很好的“念头”,华罗庚教授也说过“数缺形时少直观,形少数时难入微”,大家是否可以从形的角度来理解一下呢? (学生们似乎明白,纷纷在下面进行尝试.) 生10:ax3-3x+2≥0对任意的x∈[-2,2]恒成立,等价于ax3>3x-2恒成立,从形的角度可以理解为函数y=ax3的图像恒在直线y=3x-2的上方. 师:直线y=3x-2是确定的,函数y=ax3的图像怎么画呢? 图2 生11:当a≤0时,函数y=ax3(其中x∈[-2,2])的图像不可能恒在直线y=3x-2的上方.当a>0时,过端点(-2,-8)的函数y=ax3中参数a=1,而且通过计算发现y=x3的图像恰好与直线y=3x-2相切于点(1,1).要使y=ax3的图像在第一象限恒在直线y=3x-2上方,则a≥1,要使y=ax3的图像在第三象限恒在直线y=3x-2上方,则a≤1,故a=1. (教师在学生讲解过程中,用几何画板演示图像的变化情况,便于学生直观理解.) 师:我们从形的角度理解了生8做法中所取的x=1正好是y=ax3的图像与直线y=3x-2的切点,夹逼出参数a的值是必然的.为什么这里的参数a是一个具体值呢?这个题目特殊在哪里呢? 生12:这道题特殊在过端点(-2,-8)的函数y=x3恰好与直线y=3x-2相切.如果不相切的话,就应该是范围. 师:很好!你通过图像从形的角度完美地解释了a为定值的原因.那么,你能不能改编一下这道题,使得a的值是一个区间范围? 生12:只要将直线方程改一下,让它还经过点(-2,-8),改变斜率(斜率小于3)就可以了,譬如将斜率改为2,直线方程为y=2x-4,当a>0时,不等式变为ax3≥2x-4,即函数的解析式变成了f(x)=ax3-2x+4. 师:非常好!让我们为她的精彩改编鼓掌! 师:通过这道题的学习,对于不等式恒成立求参数问题一般解决的策略是什么?请同学们尝试对图1中的认知网络图进行补充. 并引导学生补充完整图1中的认知网络(如图3所示): 图3 教师投影练习题: 1)设函数f(x)=ax3-3x+1(其中a∈R),若对于任意的x∈[-1,1]都有f(x)≥0成立,则实数a=______. 2)设函数f(x)=(ax2+x)ex(其中a∈R),其中e是自然对数的底数,若函数f(x)在x∈[-1,1]上是单调增函数,求实数a的取值范围. 3)设函数f(x)=(m-3)x3+9x,若f(x)在区间[1,2]上的最大值为4,求m的值. 上述3个练习让学生当堂完成.教师通过课堂观察到:学生完成情况较好,正确率较高. 笔者听了这节习题讲评课,觉得这是一节难得的好课,因此很想了解教师对这节课的设计意图和教后体会,也想了解学生通过本节课的学习感受.于是对教师进行访谈,并对学生进行问卷调查. 笔者:您这节课是一节习题研究课,为什么会选用这道题? 师:1)这道题是我们最近高三数学测试题上的一道填空题,其实是2008年江苏省数学高考第14题的改编,考查的知识和数学思想方法很丰富,学生有必要理解和掌握.2)从测试反馈来看,正确率不高.课前我让每位学生在纸上写下考试时的解题思路.经过批阅,发现大多数同学选择直接研究函数f(x)的最值,但由于需要对a进行分类讨论,过程复杂,有不少同学出现错误或放弃;也有一部分同学选择先参变量分离再求最值,但由于还需要对x进行分类讨论,正确率也不高;只有个别同学利用“特殊值效应”将参数的范围缩小,再继续做.针对学生的答题情况,我觉得选用这道题来研究是有必要的. 笔者:您的教学活动的设计意图是什么? 师:1)暴露学生的错误观点及学生在解题过程中的思维障碍,通过学生独立思考与合作交流,掌握不等式恒成立求参数范围(或值)的问题的方法,特别是利用“特殊值效应”缩小参数的范围减少分类的方法.2)通过这样的研究课,培养学生的反思、质疑意识和发现问题的能力,做一个会思考的人. 笔者:通过这节课的教学,您有何体会? 师:这节课学生的学习活动有两处超出了我的预设,这是课前没想到的:1)生8的解法直接通过取特殊值将参数a的值夹逼出来;2)“同学们做完这道题后有没有什么困惑?”只是平时上课的习惯性一问,却问出了两个值得去探究的问题,又得到了数形结合的方法. 笔者:您认为教学效果如何? 师:我个人认为实现了教学目标,又有新的生成,学生通过不断探究揭示了数学本质,从课堂尝试练习来看,学生完成还是不错的,个人对本节课比较满意.教学效果究竟如何?还要由学生来评价. 为了便于对学生进行调研,笔者设计了如表1所示的问卷,发放给上课班级的学生,共发放48份,收回有效问卷45份. 表1 学生调查问卷 经统计分析表1中的这6个问题,选A的比例分别为93%,84%,84%,98%,100%,93%,可以看出学生喜欢这样的课堂:不仅是有收获的,而且是被尊重的.如此学生自己的想法才能得到充分展示. 笔者听了这节课及课后进行访谈调查,心里无比激动.笔者一直思考的问题“如何提升习题研究课的有效性?”,这节课无疑作了一个示范. 不少教师出于某些功利性目的的需求,习题教学就是向学生讲解一道又一道的题目,介绍一种又一种的解题方法,不关心学生的思维障碍在哪里,无视学生的基础和感受,这种教学助长了学生思维的被动性,学生往往只会记下这道题目的正确答案,却很少在课后追问为什么,因而他们记录的正确答案实际上沦为一个个毫无意义的符号.如何提升习题课的有效性?应从学生的基础出发,基于学生的认知规律,把学生的思维作为解题教学的起点,因势利导进行教学.正如案例中的教师在课前详细批阅了学生的解答过程,了解到学生的主要思路和存在的典型问题,以此作为本节课教学的起点,在课堂上暴露学生的错误观点及思维障碍,尊重学生的思维,顺其自然地帮助学生[1],引导学生独立思考与合作探究,使学生理解掌握了不等式恒成立求参数范围(或值)的问题的方法,特别是利用“特殊值效应”缩小参数范围减少分类的方法. 伊列雷斯教授认为动机维度是学习中的一种重要和不可或缺的要素,它以动机、情绪、态度和意志模式出现,至少与学习的内容和结果同等重要.动机常常会是一个“认知不协调”问题,即一个人经历的事物是与他的观念相冲突的.而“认知不协调”问题常产生于问题驱动[2].本案例中,教师在学生思维“最近发展区”倡导思维风暴,通过“这部分的解答过程有问题吗?如何纠正?”“这一思路该如何完善呢?”“不等式f(x)≥0恒成立问题还可以用什么方法来解决?”“生4的做法有错吗?错在哪里呢?”“为什么要讨论呢?”“你能说说完整的解法吗?”“是怎么想到分类讨论的?又是怎样讨论的?讨论的依据是什么?”“有没有方法来减少讨论,甚至避免分类讨论呢?”“有没有什么困惑?”“你能不能改编一下这道题,使得a的值是个范围?”等一系列元认知提问,引发认知冲突,激发探究学习的动机,让学生在独立思考的基础上合作交流,使学生自行解决“思维障碍”,提炼了“不等式恒成立求参数值(范围)”的常见思想方法,完善了学生的认知结构,而且学生认识到教师是真诚地对大量的想法和回答感兴趣,学生增加了学习数学的幸福感,有利于学习动机的激发与持续. 启发性质疑是质疑教学的基本特征.通过给学生一个启发提示语或问题,引导学生反思自己的数学活动经验,从而促使学生自己进行探究,并把通过探究重新获得的新认识说出来,让原有的思维经验获得新的生命力.本案例中教师不断通过问题引导学生质疑和反思,自然生成了一个个源于学生的“念头”,并进行有效地探究,特别是在学生得到了题目的正确解答后,并没有到此结束,而是于无疑处生疑,“迫使”学生提出了两个困惑,激发学生的愤悱之情,自觉开展微型探究,促进了学生的深度学习.从形的角度来思考问题,不仅完美地诠释了答案,揭示了数学的本质,更进一步提升了学生的思维层次和数学素养. [1] 伊列雷斯.我们如何学习——全视角学习理论[M].孙玫璐,译.北京:教育科学出版社,2010. [2] 波利亚.怎样解题——数学教学法的新面貌[M].涂泓,冯承天,译.上海:上海科技教育出版社,2002. 2017-10-10 江苏省教育科学“十二五”规划课题(B-b201502285);江苏省教育科学“十三五”规划课题(D/2016/02/244) 花 奎(1972-),男,江苏仪征人,江苏省特级教师.研究方向:数学教育. O122.1 A 1003-6407(2017)12-04-05
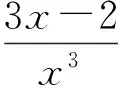


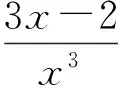

1.2 反思观察,优化方法




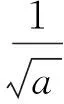

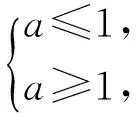
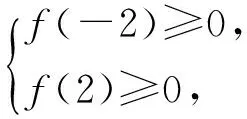
1.3 无疑生疑,揭示本质

1.4 总结应用,形成经验
2 课后访谈与调查
2.1 与教师的访谈交流
2.2 对学生的调研分析

3 听课及访谈调研后的思考
3.1 基于学生基础,把学生的思维作为解题教学的起点
3.2 基于对话交流,利用元认知提问驱动学生学习的动机
3.3 基于质疑反思,通过微型探究揭示数学本质

