以“本”为据 以“思”促教——高三数学解题教学的实践与思考

●

(浙江师范大学附属萧山第二高级中学，浙江 杭州 311251)

●朱 哲

(浙江师范大学教师教育学院,浙江 金华 321004)

以“本”为据以“思”促教
——高三数学解题教学的实践与思考

●范迪飞

(浙江师范大学附属萧山第二高级中学，浙江 杭州 311251)

●朱哲

(浙江师范大学教师教育学院,浙江 金华 321004)

文章从高三数学解题教学出发，结合课堂的教学情况和学生的学情，进行实践与思考，提炼出“抓住习题本质、课本知识挖掘、思维导图运用”这3个提高解题教学有效性的方法，从而培养学生的数学思维能力.

解题教学；课本挖掘；思维导图

解题教学贯穿高三复习的始终，从某种意义上说，解题教学的高效与否很大程度上决定了高三数学复习的成败.怎样的解题教学能够帮助学生夯实数学功底，提升数学素养呢？笔者结合自己的教学实践提出如下3点看法.

1 抓住本质，突破提高

高三学生在解题时常常望题生怯，只看到题目的表面而无法抓住问题的本质，此时教师就要引导学生透过问题看本质，突破解题的盲区.以下是笔者针对一类绝对值函数最值问题的教学过程：

(2017年浙江省台州市高三第一次质量检测数学试题第17题)

笔者所在学校将该题用于高三第二轮复习中的一次阶段考试，但得分率不高.与学生交流后发现学生的问题主要有以下4个方面：

1)无法呈现函数图像，不知道如何表示函数的最大值M(a,b)；

2)不知道是否需要去掉函数的绝对值，如何去；

3)尝试用绝对值不等式，但后续无法进行；

4)无法理解M(a,b)其实是一个范围.

此题的解法有好几种，考虑到绝大部分学生纠结于此题的绝对值，因此笔者在课堂中从绝对值的几何本质入手.

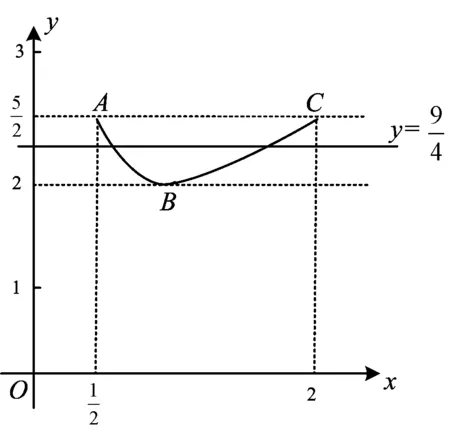
图1

为了加强学生对函数纵向距离的理解，笔者在课堂上又设计了如下两个变式：

分析有了例1的铺垫，学生很快能分析出变式1的解题思路.如图2，根据导数的相关知识得出直线AC的方程为

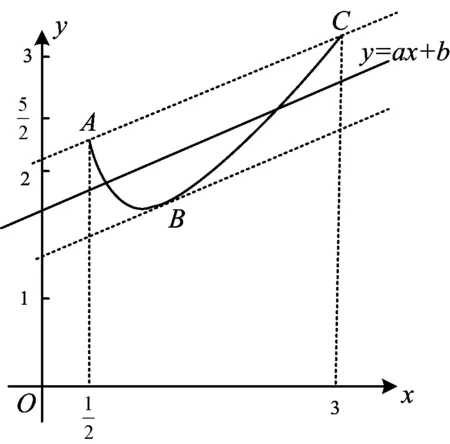
图2

过点B且与lAC平行的切线方程为

(其中θ为直线AC的倾斜角).

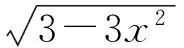
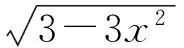
(2017年浙江省数学高考试题第17题)

图3

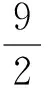
因此在教学中针对学生出错或没有思路的现象，教师可以从学生的困惑入手，引导学生看到问题背后的本质，突破问题的难点，让学生真正在数学思维上得以提高.

2 挖掘文本，举一反三

教材涵盖大量的例题和探究性活动，每道题目都可以引导学生发现相关的知识点和性质.以下是笔者在复习圆锥曲线时，结合课本例题讲解的“e2-1的性质”：

(浙江省2017届高三数学统考模拟卷第21题)

笔者分析试卷时发现：学生通过联立直线AP与椭圆的方程，根据韦达定理和垂直的两向量数量积为0进行证明，得分率较高.不过笔者在课堂中仍提出了不同的解题方法.

《数学(选修2-1)》中就向学生呈现了解答此题的方法，因此笔者重新将课本中的例题提出：

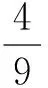
分析易得点M的轨迹方程为

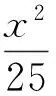
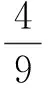
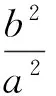
笔者再次引导学生发现点A,B不仅仅是椭圆的左、右顶点，而是关于原点对称的两个点.因此，学生由特殊转换到一般，对这一现象进行了猜想与论证，具体如下：

设点M(x,y)，点A和B关于原点对称，其坐标分别为A(m,n),B(-m,-n)，则

从而

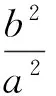
根据上述推导可以得出：

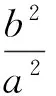
结合推论1，例3便有了新的证明方法：

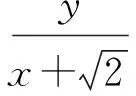
故

OP⊥BC.

图4

根据上述推导可以得出：

而这些推论在高考中也有较多的应用，笔者在教学中也再次进行运用.

(2015年浙江省数学高考理科试题第15题)

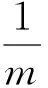
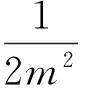
即

由于双曲线与椭圆在图形上有着相同的对称性，学生提出问题，是否双曲线中也有类似的性质？于是笔者又趁热打铁与学生一同探讨，得出双曲线中的“e2-1的性质”：

这些教学案例仅仅只是教材中一道例题的发掘延伸与应用，笔者认为教师应该在平时的解题教学中充分研读、挖掘课本，做到举一反三，真正在解题教学中拓宽学生的思路，达到解题教学的高效性，提升学生的数学素养.

3 自我监控，查漏补缺

数学学科的自我监控能力，是指学生为了保证数学学习的高效与成功，而在整个数学学习过程中，将数学学习活动作为意识对象，对其进行积极主动的计划、检验、调节和管理，从而实现学习目标的能力[1].数学自我监控能力较高的学生善于对数学思维过程和结果进行反思，从而较快掌握数学思维和解题策略.因此教学中需要加强对学生这一能力的培养，而思维导图便是一种有效的途径.

思维导图是一种利用图形来表达发散性思维的思维工具，它以中心词为出发点，充分利用箭头、直线、曲线和特殊符号等图示表达不同内容的从属关系[2].笔者认为若能在解题教学中从学生分析题目的思维导图入手，则教师就能准确找到学生解题困难的原因，保证解题教学的高效性.

以下是笔者通过分析学生的思维导图进行教学的案例：

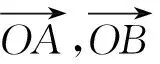
(2016年浙江省杭州市第一次教学质量检测数学理科试题第15题)

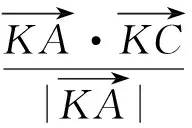
图5

( )

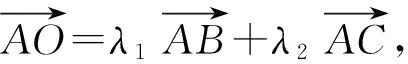
(2017年浙江省杭州市第一次教学质量检测数学试题第7题)

思维导图的运用是一种有效的教学策略，它可以帮助学生做到数学思维的自我监控，看清自我思维的漏洞，从而在自主学习中逐步形成严密的数学思维，在解题中真正达到思维训练与提高的目的.

4 结束语

弗里德曼在分析学生解决了大量的题目但还“不开窍”这一现象时指出：这些学生没有在应有的程度上分析所解的习题，不能从中分析出解题的一般方式和方法，解题常常只是为了得出答案.这指出了一条途径：通过解题过程的分析和解后反思来积累经验与类型[3].因此笔者认为高三的解题教学应该注重学生的解题思维，帮助学生分析问题的本质.同时应该注重教材，挖掘其中的知识点，在解题中进行知识点的发现、归纳和积累.这样可以有效地提高高三数学复习的效率，让学生在读题、析题、解题、悟题的过程中提升自己的数学思维素养，这也是高三解题教学所追求的境界.

[1] 陆峰.高层次数学思维与数学自我监控能力关系的研究[D].南京：南京师范大学，2004.

[2] 计雪娟.思维导图在高中数学教学中的应用设计研究[D].长春：长春师范大学，2015.

[3] 朱丽强.让学生的思维在解题研究中飞翔——高三数学解题教学的实践与思考[J].中学数学，2013(3):48-50.

2017-09-16

范迪飞(1992-)，女，浙江萧山人，中学二级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)12-09-04