老树新枝又一春——2017年浙江省数学高考立体几何解答题阅卷有感

●

(杭州第七中学,浙江 杭州 310024)

老树新枝又一春
——2017年浙江省数学高考立体几何解答题阅卷有感

●叶启垦

(杭州第七中学,浙江 杭州 310024)

2017年浙江省数学高考立体几何解答题立意平稳，有效创新，注重核心素养的考查,具有良好的区分度.文章通过对该卷中立体几何解答题的解法探究及答题情况分析，提出在平时教学中应该注重培养学生的答题策略.同时，在新高考形式下的数学复习教学更应重视完善双基，突出数学本质，实现思维回归.

数学高考；立体几何；答题策略

2017年浙江省数学高考已尘埃落定.这是30多年来浙江省数学高考第一次以文理合卷的形式呈现.试卷起点较低，循序渐进，同时顺接而下，延续着几年来数学高考卷的追求，“重思维，重本质”，整卷合乎文理合卷后的特点，凸显“文之韵，理之味”.

笔者有幸参加了2017年浙江省数学高考阅卷，亲身感受着：一张试卷承载着国家所赋予的神圣责任，一分分数寄予着千万学子的殷切希望.下面就以第19题为例，试图以一窥全，同时也谈谈个人的反思与体会.

图1

1 试题赏析

题目如图1，已知四棱锥P-ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．

1)证明：CE∥平面PAB；

2)求直线CE与平面PBC所成角的正弦值．

(2017年浙江省数学高考试题第19题)

该题考查了直线与平面平行以及线面所成角问题，背景非常熟悉，而且设问方式常规，与2016年12月的浙江省模拟卷吻合，属于意料之中的题型.命题者希望通过这种类型问题的考查，检测考生的几何空间感以及逻辑推理、直观想象、数学运算等数学学科核心素养.而且设问从基础出发，层层递进，梯度合理，兼顾原有文理生之别.两个小题之间又存在合理的逻辑关系，证明平行关系为寻找线面角铺设了道路.总的来看，该题彰显学科特色，有效创新，注重核心素养的考查.

不过，从阅卷的实际情况看，试题难度预计有一定的偏差，具有良好的区分度.本题的平均得分为8.39，除去0分试卷后平均得分为9.08，难度系数为0.56.而2016年的立体几何解答题，理科全省平均分为10.89，难度系数为0.72；文科平均分为8.66，难度系数为0.58[1].可见，这份高考卷中立体几何结构梯度自然，对不同基础、不同能力水平的学生都提供了适当的思考空间，体现了较好的区分度，凸显了试卷的选拔功能，同时难度总体是有所提升的.当然，到底是这道题本身的相对难度提升了，还是新高考下学生整体水平有所下降，值得我们进一步研究与思考.

2 解法探究

本题满分15分，其中第1)小题6分，第2)小题9分.

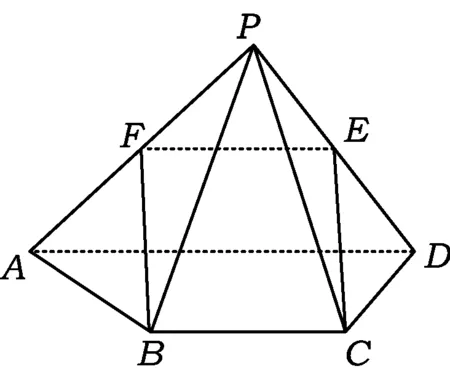
图2

2.1 第1)小题解法探究

证法2(面面平行)如图3，取AD的中点N,联结EN,CN,则CN∥AB,EN∥AP,从而面CEN∥面PAB，于是CE∥面PAB.

图3 图4

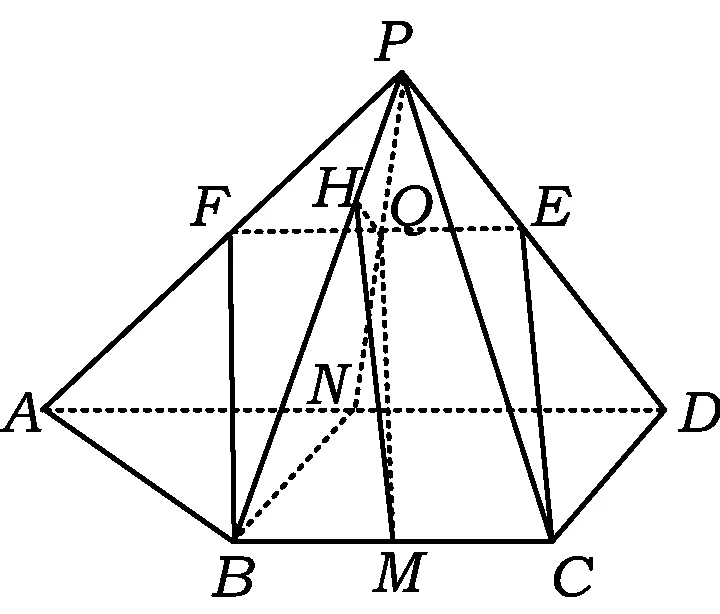
图5

2.2 第2)小题解法探究

解法1(几何法)如图5，分别取BC，AD的中点M，N,联结PN交EF于点Q，联结MQ．因为E，F，N分别是PD，PA，AD的中点，所以Q为EF的中点，即在BCEF中，

MQ∥CE．

由△PAD为等腰直角三角形，知PN⊥AD；由DC⊥AD，N是AD的中点，知BN⊥AD，从而AD⊥平面PBN.又BC∥AD，于是

BC⊥平面PBN，

进而可知平面PBC⊥平面PBN．

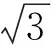
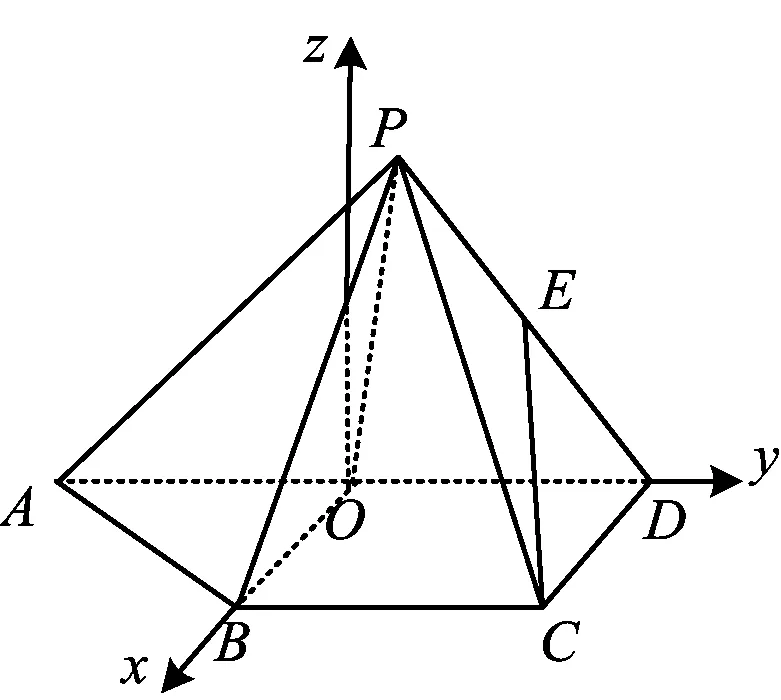
图6

解法2(空间向量坐标法)如图6，取AD的中点O，联结BO,PO,易知PO⊥AD,BO⊥BC,从而

PO⊥BC,

于是BC⊥平面POB,进而PB⊥BC.设BC=1，则

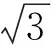
从而二面角P-AD-B的平面角∠POB为120°.

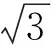
评注从阅卷情况看，采取空间向量建系的方法最容易得分，根据建系位置的不同，得到向量的坐标有些许区别.

图7

解法3(等体积法)如图7，过点E作EO⊥平面PAD,联结CO,则∠ECO就是直线CE与平面PBC所成的角.

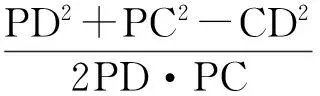
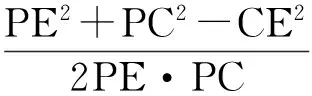
由等体积法得点D到平面PBC的距离为1,因为E为PD的中点，即

所以

3 答题情况分析

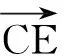
总之，从数学核心素养的角度看，本题的答题情况反映出以下几个问题：

1)直观想象是数学核心素养的重要组成部分，良好的直观想象能力有助于学生深刻体会数学的创造过程，形成严谨的逻辑思维能力.而从本题的答题情况看，学生的直观想象能力总体相对较薄弱，立体空间感较差，不能正确把握图形结构.当然，审题马虎也是问题之一.

2)运算能力作为学生学习数学的基础，是构成数学抽象结构的基本元素.而学生在求解过程中表现出运算能力较弱，从而导致计算失误，特别是坐标的求解有很大问题.

3)数学证明、概括的表述自有学科特殊的语言体系、特定的符号体系——数学语言体系,这种表述形式应贯穿于数学证明、解答过程的始终[2].可以说，学生解题的过程正是数学语言的呈现过程.而在本题的解题过程中，不少学生存在语言表述不清、逻辑混乱的情况，答题不规范，随心所欲——随意删除、字迹潦草，这些应该是平时不够重视的结果.

4 基于评分原则下的答题策略

评卷者应该如何科学评卷呢？笔者认为：应该与命题者的最初命题意图保持一致，只有真正做到科学地评卷，才能实现命题者最初命题考查的目的，才能对我们的教学进行有效地引导.本题通过立体几何题考查学生的数学思维方式与计算能力，评阅过程中也尽可能体现“重思维，重本质”的意图，因此，严格控制解答题的评分误差，是提高考试信度的保证.因此，作为评卷者应该遵从以下评分标准原则：1)解答方法的普遍性；2)采分点符合知识点与关键表达、结论的必要性和充分性；3)分值向能力倾斜原则；4)不同解答方法的等值性；5)表达文字、逻辑语言规范性[3].只有正确执行落实这些基本评卷原则，才能进行有效阅卷，做到公平公正.

基于以上评分标准原则，在教学中应该让学生形成以下几点答题策略：

1)踩点给分，关注的是学生的思维过程.学生在解题过程中所呈现的思维过程就成了评分的主要得分点.

以本题的第2)小题为例，在评卷过程中，3种常见解法的评卷给分点确定如下：

①几何法：找准哪个角就是所求的角；正弦值的比例关系；计算结果.

②坐标法：如何建立空间直角坐标系——关键在于有建系的思想；向量以及平面法向量的正确求法和表述；所求角与向量夹角之间的联系——向量的内积公式.

只要能表达出解题的思维过程，就是得分点.而一道题所涉及的主要概念和公式正是思维呈现的主要形式.因此，不能因为一道题不能解答，就放弃表达自己的思维过程.总之，有论证表达的过程，总比没写好；有解题思路比没想法好.

2)等值性，即关注给分的合理性.数学往往有多种解法，多种解法之间要有一定的平衡，相应的步骤会给出相应的分数值.而学生在解答过程中提供两种方法是不会重复给分的，择高给分.因此，在考试答题时，应利用好有限的时间作答.

3)表达文字、逻辑语言规范性.数学的语言表述，反映出学生数学的逻辑能力与水平.因此，在答题时，字尽量写端正，更重要的是整个解答结构要整洁、清晰，更不要轻易涂改.

5 新高考形势下的数学复习策略

1)回归教材本身，完善双基结构.从这样一份表述简洁、立意精准的卷子可见，日常的课堂教学，特别是高三数学复习要落实学生的基础知识、基本技能.核心素养的培养并不排斥基础知识、基本技能的落实与掌握.双基是教学活动正常施行的载体,也是学生数学思维训练的工具.没有了双基，基于核心素养的教学活动就成了无源之水；没有了双基，基于数学思维的数学解题也就成了无本之木.而且，从近几年的高考试卷看，命题者越来越注重对概念的准确理解的考查以及基本图形结构的准确把握，因此，在高考复习中，有必要形成准确、系统的知识结构，从而让学生掌握得更扎实.当然，每个学生的基础薄弱点都有所不同，需要有针对性地进行训练与辅导.

2)突出数学本质，实现思维回归.高考毕竟不是学考，有一定的选拔性，不同层次的高校需要不同层次的生源.近几年的数学高考都延续着“重思维，重本质”的特点.因此，关注数学本质，着力于提升学生的数学核心素养，才是真正的教学之道.而要突出数学本质，需要挖掘一个概念背后的来龙去脉，需要理清一个方法的真正意义，而非停留在简单地重复操练与粗暴记忆上.平时的复习要注意思维的训练，每完成一道题后教师都能指导学生再反思：本道题重要的步骤是什么？平时要注意解题的规范化，这本身就体现了学生数学思维的严密性，平时考试的批改可以适当给正确思路的分数，以训练学生不留空白的解题习惯.

同时，不猜题，不押题，深刻解读和领会当年的考试说明，研究当年的高考模拟卷，以真正理解命题者的意图.这样，才能知道“从哪里来，到哪里去”，有的放矢.

3)关注通式通法，渗透巧解妙解.“重思维，重本质”的高考命题方向，在解题方法的考查上也更注重通式通法.以本题为例，基本的几何法、常规的辅助线添加法、空间直角坐标建系都是平时应重点训练的方法.因此，在平时的教学中，可以通过变式练习，加强通式通法的训练.当然，通式通法并不排斥巧解妙解,特别是在解决选择题、填空题时，往往不必“小题大做”，而应该追求解题的效率.另外，准确合理的数学语言表达是学生顺利掌握一种方法的基本呈现方式，在平时的课后反馈中要及时纠正解题过程中出现的逻辑混乱的语言表述.

[1] 卢明．一样的风景 更高的要求——2016年浙江数学高考立体几何题评析[J]．中学教研(数学)，2016(10)：26-31．

[2] 朱伟义，曹凤山.大道至简 悟者天成——2016年浙江省数学高考试题简析及有关高考复习的思考[J].中学教研(数学)，2016(8)：36-39.

[3] 陈子志.体会高考国家统一命题的基本原则与评分参考标准[DB/CD].http://www.china.com.cn/education/2016-01/14/content_37576927.htm,2016-01-14.

2017-09-29

叶启垦(1976-)，男，浙江杭州人，中学高级教师.研究方向：数学教育.

O123.2

A

1003-6407(2017)12-35-04