学生自主学习实践中教师的度与量

赵忠新

学生自主学习实践能力的培养得到广泛重视，而在具体的情境中，我们能不能对学生的“创见”及时做出适当的反应，对学生自主学习实践的意识和能力有很大的影响。

案例1：一次《异分母分数加减法》教学活动后，小张老师对我说：“我觉得这节课有一个遗憾，就是你发现有一些学生通分时没有用分母的最小公倍数作公分母，却没有要求他们都改过来。”我给他讲了关于这件事与学生的一段故事。我当时遇到这种情况时，也要求学生用几个分母的最小公倍数做公分母。学生振振有词：“书上很明确：‘一般用原来几个分母的最小公倍数作公分母，我觉得这里不需要，因为5/6-2/9=5×9/54-2×6/54交叉一乘很省事，我只要约分就行了。”我不再强调，因为他们并不是不会通分，只是想按照自己的意愿尝试一下，此后他们用这种方法计算兩天后，就自己纠正过来了。

体会与反思：包容和善待学生自主学习的“成果”。学生在解决问题的过程中，经过自己的思考，会得出自以为合适的方法，虽然不尽完善和优化，但是他们不是因为对知识不理解而产生的“误解”，我们要理解学生对自己所思所得的“敝帚自珍”心理，采用冷处理，避免因心理上的对立，让他们在实践中淡化己见，优化方法。

案例2：在五年级质量检测的阅卷中，有两名教师为一题争执起来。题目是：请在下面的正方形中画出一个最大的圆。张老师认为学生做对了，因为他画出了一个非常标准的最大的圆；李老师认为学生做得不对，因为这题的关键是确定圆心，要连接对角线，以交点为圆心，他没有交代出圆心是怎么确定的，所以纯属碰运气。我仔细看了试卷，暗暗为学生叫绝：“他是个聪明的孩子，他找圆心的办法确实没有画出来，但是他确实用了自己的办法找到了”。原来，这名学生的试卷上有纵横两条折线，他是利用试卷纸的透光性，利对折后的折痕交点确定了圆心。我说：“更加可贵的是，他很细心，手也很巧，他的折痕只比图形稍微长出一点。试卷上的另外一题‘把一张长方形纸对折三次后，每份是原来的几分之几他肯定也做对了。”一查，果然是。我建议他们拆封后，要对这名同学进行鼓励和指导。

体会与反思：发现和欣赏学生自主实践的“成果”。很多时候，我们总是抱怨：学生的动手能力差，不能用自己的办法解决实际的问题，而当学生真正动手，在实践中解决问题的时候，确是我们以自己的思维来评判他们，无意中对他们造成打击和压抑。

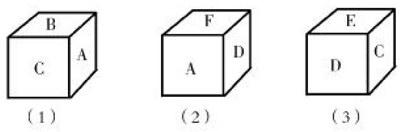
案例3：学习正方体和长方体后，学生的课外习题中有一道：如下图，一个正方体的6个面分别写着A、B、C、D、E、F六个字母，根据下面的三种摆法，判断哪两个字母在相对的面上。

学生介绍的时候基本上都是排除法：A的对面不可能是B、C、D、F，只能是E……有一位学生拿出一块橡皮：“我用一块橡皮，按照（1）写上字母，在调整到（2），A在正面，上面和右面空白的写上F和D，就解决了。”有的同学嘲笑他，太麻烦了。我热情地表扬了她，因为她不仅动了脑，还动了手。

体会与反思：鼓励和推崇学生自主实践的“成果”。长期以来，学生的学习一直偏重于思维的训练，我让学生做本题的目的就是希望培养学生空间观念和思维能力，这名学生能够利用长方体和正方体都有三组相对的面的特点，自觉地把分析思维和操作实践相结合，这不正是学生运用知识解决实际问题能力的体现吗？

案例4：教学《公倍数和最小公倍数》时，现行的苏教版教材没有把短除法作为必修内容，而是采用列举法：可以先列举出6和9的倍数，再从中找出6和9的公倍数、最小公倍数；也可以找出9的倍数，再从中找出6和9的公倍数、最小公倍数。在练习题“找出每组数的最小公倍数。6和10，8和12，10和25，20和30”。做完后，我请最先做完的学生介绍自己的方法。很多学生采用先找大数的倍数，再从中找出他和另一个数的最小公倍数的方法：“我先用10÷6”，不行；再用20÷6，不行；再用30÷6=5，30就是6和10的最小公倍数。”这种方法得到同学的一致认同，所以，我们就给它起名“大数翻倍法”，在全班推广。

体会与反思：宣传和推广学生自主实践的“成果”。学生自己的见解和方法得到重视，得以推广，是对学生自主学习能力培养和促进的最好手段。