正多边形与其同心圆有关的两个性质的推广研究

辽宁省黑山县第一高级中学数学组(121400) 刘大鹏

正多边形与其同心圆有关的两个性质的推广研究

辽宁省黑山县第一高级中学数学组(121400) 刘大鹏

文 [1]中获得的主要结果是：正多边形的内切圆(或外接圆)上任意一点到各顶点的距离平方之和为定值,正多边形的内切圆(或外接圆)上任意一点到各条边的距离平方之和为定值.[1,2]

文[2]对这两个性质进行了推广,获得正多边形的同心圆(即圆心在正多边形中心的圆)也有这两个性质.(I)正多边形的同心圆上任意一点到各顶点的距离平方之和为定值;(II)正多边形的同心圆上任意一点到各条边的距离平方之和为定值.[2,3]

本文以正方体、正四面体为研究对象,把性质(I),(II)在空间推广,得到

定理1设球面O为正方体ABCD-A1B1C1D1的同心球面(即球心在正方体中心的球面),P为球面O上任意一点,则P到正方体各顶点的距离平方之和为定值;P到正方体各面所在平面的距离平方之和为定值.

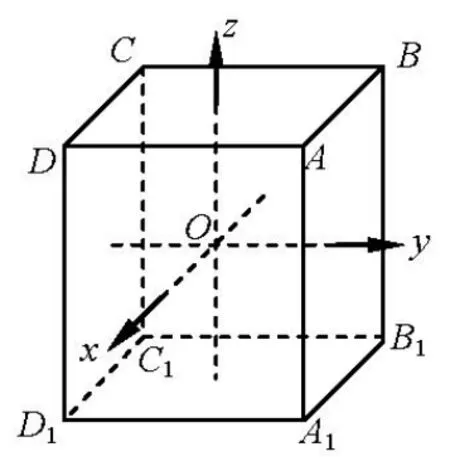
图2

证明 设正方体棱长为2a,建立如图空间直角坐标系,球面O方程：x2+y2+z2=R2,P(x0,y0,z0),A(a,a,a,),B(-a,a,a),C(-a,-a,a),D(a,-a,a),A1(a,a,-a),B1(-a,a,-a),C1(-a,-a,-a),D1(a,-a,-a).于是

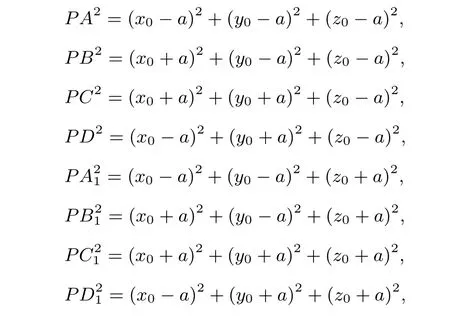
所以∑PA2=8(x20+y20+z20)+24a2=8R2+24a2为定值.

各面方程：面AA1D1D:x=a,面BB1C1C:x=-a,

面ABB1A1:y=a,面CDD1C1:y=-a,面ABCD:z=a,面AA1B1C1D1:z=-a.

∑d2i=(x0-a)2+(x0+a)2+(y0-a)2+(y0+a)2+ (z0-a)2+(z0+a)2=2R2+6a2为定值.

定理2 设球面O为正四面体ABCD的同心球面,P为球面O上任意一点,则P到正四面体各顶点的距离平方之和为定值;P到正四面体各面所在平面的距离平方之和为定值.

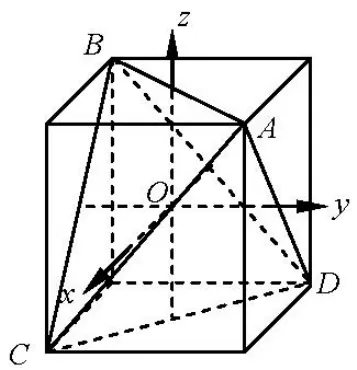
图2

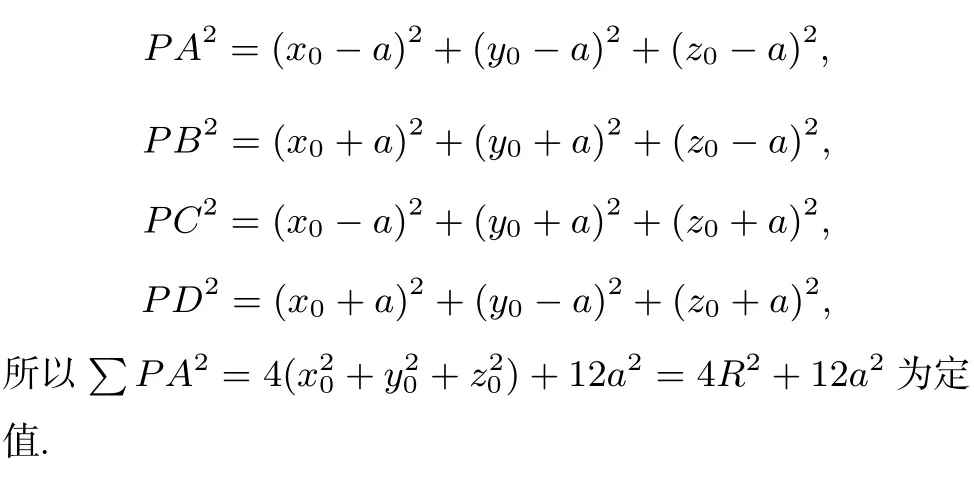
由正四面体各面分别与正方体的某一条体对角线垂直,得面ABC,面ACD,面ABD,面BCD的法向量分别为(1,1,1).

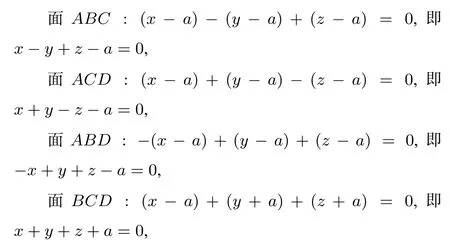
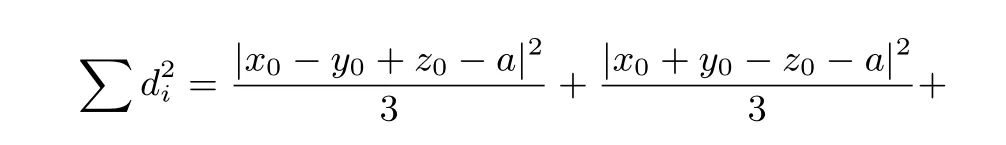
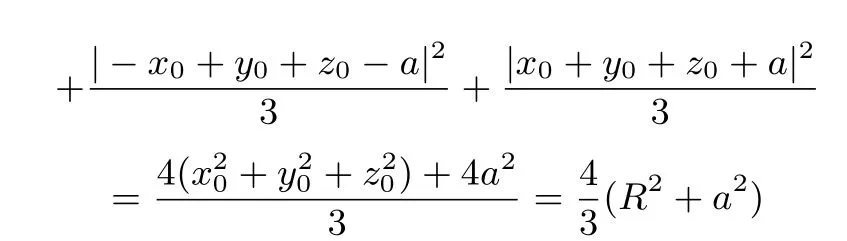
为定值,证毕.

猜想：上述性质对正八面体、正十二面体、正二十面体也成立.

[1]马俊华.正多边形的内切圆和外接圆的一些性质[J].中学数学月刊, 2007(8).

[2]徐道.正多边形与其同心圆有关的几个性质[J].中学数学研究, 2008(9).

[3]徐道.正多边形与其同心圆有关的两个性质的指数推广[J].中学数学研究,2010(2).