一题多解—一道不等式恒成立问题的赏析

广东广雅中学(510160) 林才雄

一题多解—一道不等式恒成立问题的赏析

广东广雅中学(510160) 林才雄

一道2017年河南省郑州市高三第一次质量预测的函数压轴题,笔者通过不同的角度,发散思维,对该含参不等式恒成立问题进行了多维探究,呈现了该问题的一题多解的魅力.

不等式,一题多解,发散思维.

题目已知函数f(x)=(1-mx)ln(1+x).

(1)若当0＜x＜1时,函数f(x)的图像恒在直线y=x上方,求实数m的取值范围;(2)从略.

解法1(参考解法)(1)令

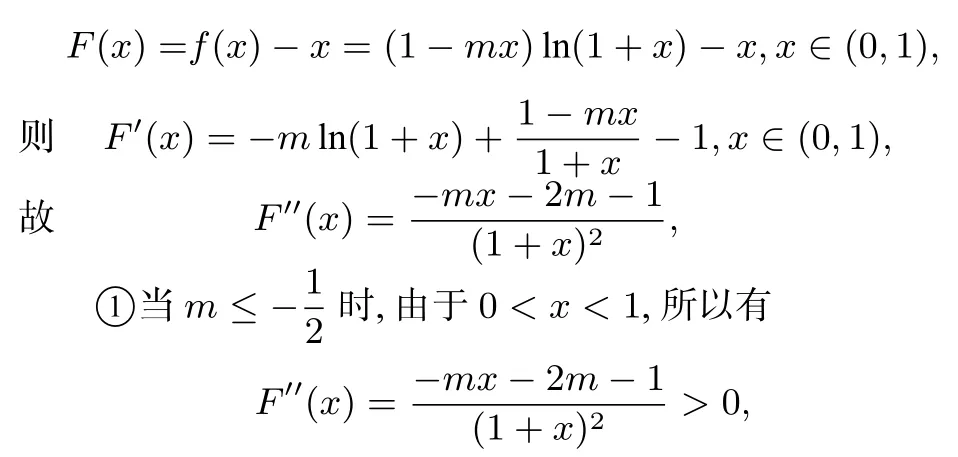
于是F′(x)在(0,1)上单调递增,从而F′(x)＞F′(0)=0,因此,f(x)在(0,1)上单调递增,即F(x)＞F(0)=0符合题意;

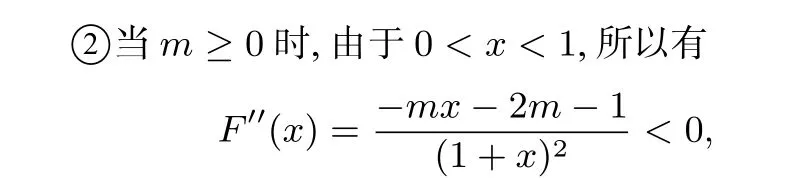
于是F′(x)在(0,1)上单调递减,从而F′(x)＜F′(0)=0,因此,f(x)在(0,1)上单调递减,即F(x)＜F(0)=0,不符合题意;则当x∈(0,x0)时,于是F′(x)在(0,x0)上单调递减,从而F′(x)＜F′(0)=0,因此,f(x)在(0,x0)上单调递减,即F(x)＜F(0)=0,不符合题意.

综上,可知所求的实数m的取值范围是

从上述解答过程,大家可以发现,该解法主要是通过作差构造函数,并通过两次导数的符号的判断,分类讨论的方式,对参数m的取值进行了研究,从而解决了该问题.主要特点是构造的函数F(x)=f(x)-x= (1-mx)ln(1+x)-x,x∈(0,1)的二次导数的符号的确定取决于一个“伪一次函数”y=-mx-2m-1,并借助于函数F(x),F′(x)在x=0处的特殊值,即F(0)=F′(0)=0,从而通过分类讨论参数m,来达到解决问题的目的.可以发现这种处理方法的关键在于挖掘出F(0)=F′(0)=0.

显然该解法一开始不易想到,具有一种让人“众里寻他千百度,蓦然回首,那人却在灯火阑珊处”的意境美!而且让人感觉到了那种“山重水复疑无路,柳暗花明又一村”的豁然开朗!

一个巧妙的解答,引起了笔者对该问题的兴趣与思考,并深入探究其内在的魅力.以下我们从不同的角度对该问题进行处理,多维度地赏析它.

视角一 分离参数 由于该问题本质上是属于含参的不等式恒成立的问题,故可以考虑分离参数的方法.首先证明两个常用的结论：

引理1对任意的x＞1,不等式恒成立.

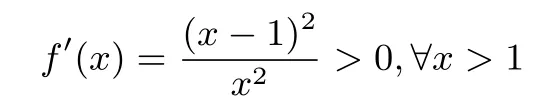
恒成立,所以函数f(x)在 (1,+∞)上单调递增,所以f(x)＞f(1)=0,即

引理2 若函数f(x)和g(x)满足下列条件：

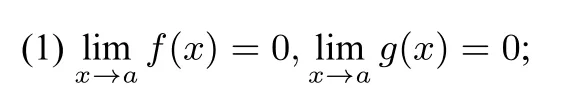
(2)f(x)和g(x)都可导,且g′(x)/=0;

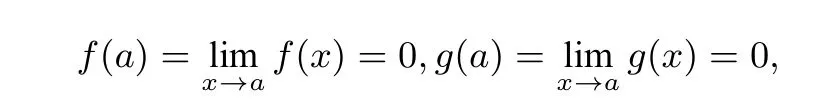
所以有

证明 由(2)可知,f(x)和g(x)都是连续函数,所以

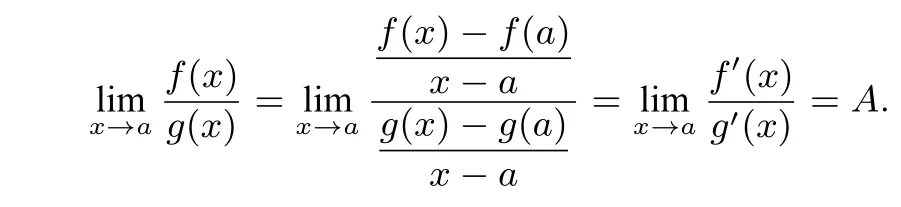
解法2(视角一)由题意可知,原问题等价于“不等式(1-mx)ln(1+x)＞x,∀x∈(0,1)恒成立”,所以有

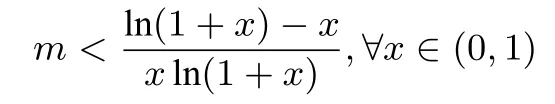
恒成立,构造函数

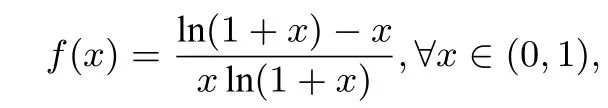
则由引理2,可知

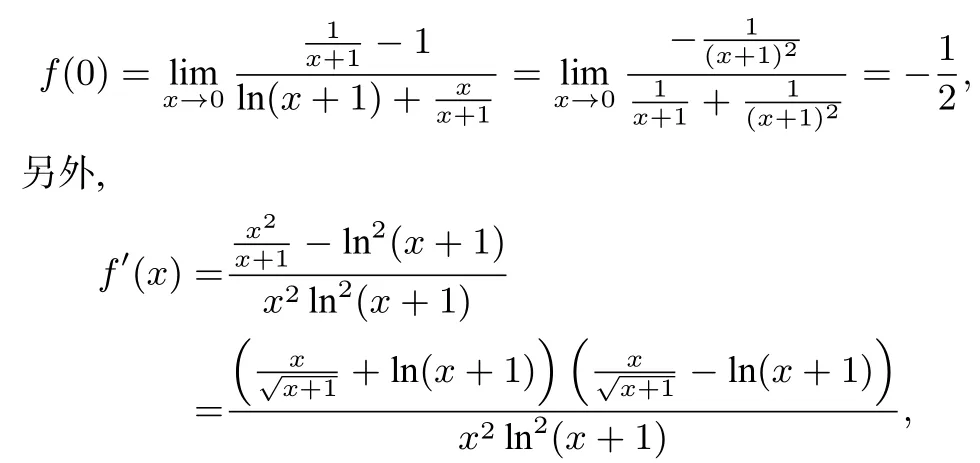
由引理1,可知

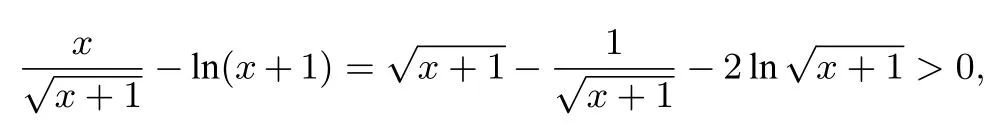
x∈(0,1),故当x∈(0,1)时,f′(x)＞0,即f(x)在(0,1)上单调递增,故

视角一赏析,我们都知道分离参数法是解决这类含参不等式恒成立问题的通性通法,所以从这个角度出发是比较常规的想法,但该问题有两处地方容易卡住我们的思路,一处是f(0)的值,这里是型的,考虑使用洛必达法则来处理;另一处是f′(x)的符号的判断,要借助对数平均不等式的一个变形来处理,对解题人来说比较困难,要熟悉并熟练运用各种常见的不等式.

视角二 数形结合 可以考虑转化为两个函数的图象的位置关系问题,其中一个为一次函数.首先证明一个结论：

引理3 对于任意的x＞0,不等式恒成立.

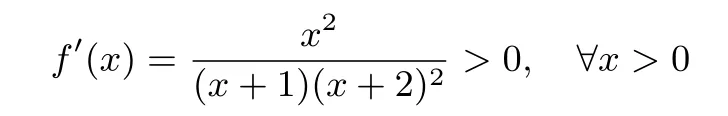
恒成立,所以函数f(x)在 (0,+∞)上单调递增,所以

解法3(视角二)由题意可知,原问题等价于“不等式

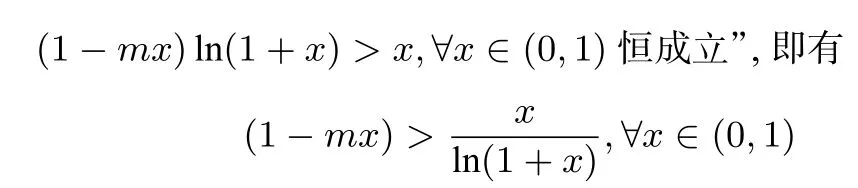
恒成立.

则问题等价于“当x∈(0,1)时,函数g(x)=1-mx的图像恒在函数的上方”,由引理2,可知

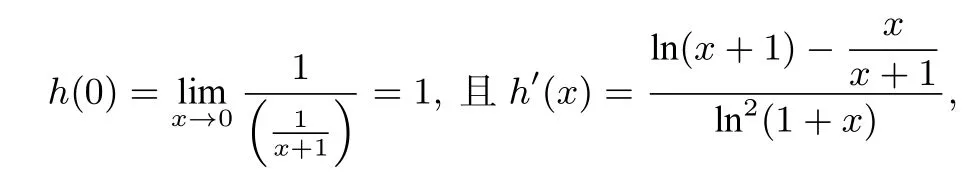
由引理3的推论,可知h′(x)＞0,另外,有

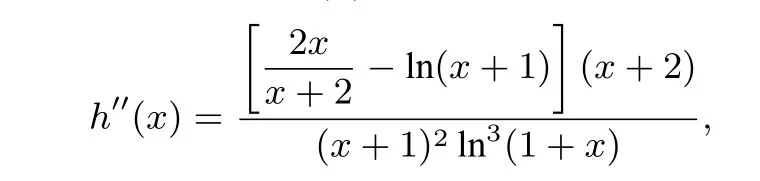
则由引理3,可知h′′(x)＜0,所以h(x)在(0,1)上是单调递增且上凸的函数.

又因为g(0)=1,所以问题等价于g′(0)=-m≥h′(0),而由引理2,可知

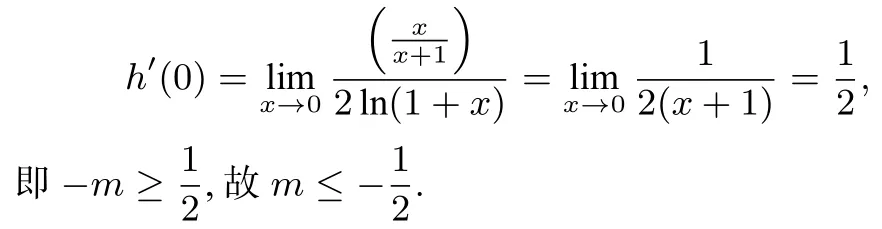
视角二赏析,该问题通过变形,可以转化为两个函数的图象的位置关系问题,其中一个为一次函数.此时,利用数形结合,从动态的角度入手处理该问题,这也是一种很形象直观而且简单易懂的方式,不过此时,使用数形结合的方法,也可能会遇到两个容易误导我们的解题思路的问题,一处是h(0)的值,这里是型的,考虑使用洛必达法则来处理.如果没有使用洛必达法则计算出h(0)=1,而想当然地认为h(0)=0的话,就容易出错;另一处是h′′(x)的符号的判断,这里通过变形,可以证明h′′(x)＜0,即说明了函数的凹凸性是上凸的,如果没有对函数h(x)的凹凸性进行判断,也容易出现直接计算h(x)在区间两个端点的连线的斜率,从而得出的典型错误.

一个有趣的问题,不同的解题角度,殊途同归,让我们感受到了数学一题多解的无限魅力.学习数学,一定不能拘泥于某种解题方法,有时候,尝试从不同的角度去思考问题,你可能会欣赏到完全不同的风景,感受到完全不同的乐趣.

[1]马丽娜,刘烁.关于洛必达法则证明的几点补充[J].青海大学学报(自然科学版).2011(29).

[2]邓军民.例谈对数平均不等式在高考中的应用[J].广东教育(高中版).2014(5).