三类传球问题的对应解法*
武汉华中师范大学数学与统计学学院(430079) 陈 欣 胡典顺
三类传球问题的对应解法*
武汉华中师范大学数学与统计学学院(430079) 陈 欣 胡典顺
传球问题是排列组合中的经典名题,在许多中学数学刊物中,有关传球问题的研究多数仅限于对传球方式不加限制的情况.对此,笔者做了进一步思索,举一反三,对传球方式加以限定,得到了三类传球问题,并通过建立一一对应的数学模型,将传球问题转化为我们已经解决的熟悉问题,得到了不同限制条件下三类传球问题的对应解法.
题型一m(m≥3)个人A1,A2,...,Am围成一圈相互传球,首先由A1发球作为第一次传球,经过n(n≥3)次传球,球又回到A1手中,试求所有传球方式的种数an.
题型二m(m≥3)个人A1,A2,...,Am围成一圈相互传球,规定每次只能把球传给相邻的人,首先由A1发球作为第一次传球,经过n(n≥3)次传球,球又回到A1手中,试求所有传球方式的种数an.
题型三m(m≥6)个人A1,A2,...,Am围成一圈相互传球,规定每次只能把球传给与自己不相邻的人,且每人至多只传一次球.经过4次传球,球又回到A1手中,试求所有传球方式的种数Am.
1.题型一⇒染色问题
此类传球问题对传球方式不加限制,一般地,可以通过分类讨论找到数列{an}的递推关系式,再进行求解.由于持球人不能把球传给自己,只能传给其他m-1个人中的任何一个,这一类型的传球问题与“染色问题”有着千丝万缕的联系(详见文[1]).
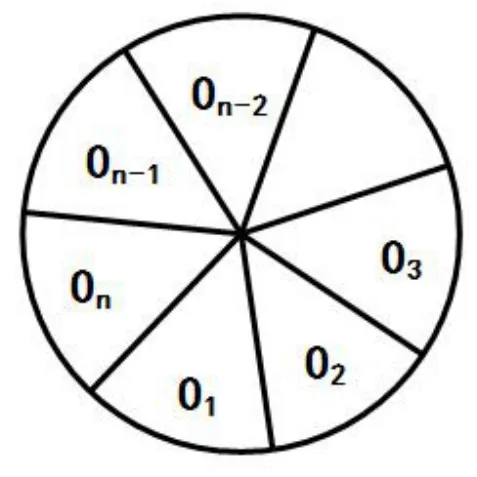
图1
建立对应关系
我们将此问题与“染色问题”建立对应关系.如果把从A1开始传球最后回到A1手中每个环节的人员按照传球次序顺次放入图1中对应的n个区域O1,O2,...,On(n≥3), (其中起始的A1和结束的A1都放入O1区域),由于持球人不能把球传给自己,故相邻两区域的人员不同,那么问题本质就是:用m(m≥3)种颜色A1,A2,...,Am给图1中的n(n≥3)个区域O1,O2,...,On染色,要求相邻区域不同色且区域O1的颜色固定的所有染色方法.
问题解答
设an为符合要求的染色方法数.则易知a3=(m-1)(m-1).不妨设n≥4,规定O1区域必须染A1这种颜色,O2与O1不同色,O2有m-1种染法.同理,O3与O2不同色,O3有m-1种染法,...,On与On-1不同色,On有m-1种染法,这共有(m-1)n-1种不同染法.但以上染法中包含了O1与On同色的情形,此时可将O1与On视为同一个区域,这样的染法恰为an-1种,因此我们得出:
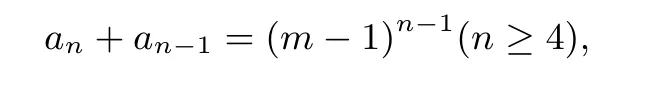
可通过构造等比数列求得:
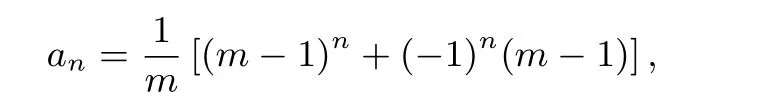
由于每一种染色方案对应一种传球方式,故符合要求的传球方式有种.
染色问题是我们非常熟悉的题型,将传球问题转化为染色问题后,题目变得更加直观、浅显.
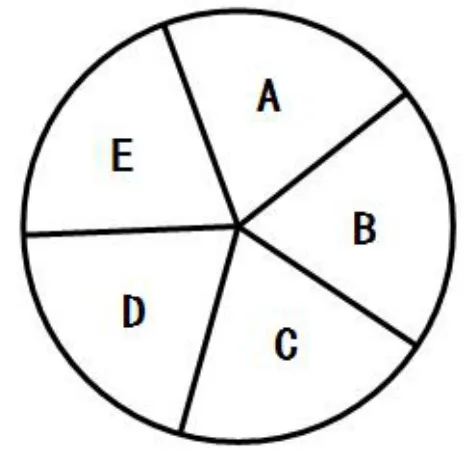
图2
例1 4人进行传球练习,要求每人接球后再传给别人,由甲开始发球,并作为第一次传球,经5次传球后,球又回到甲手中,问:共有多少种传球方式?
可将此题转化为:用红、黄、蓝、绿4种颜色,给图2区域染色,规定A区域染红色且相邻区域的颜色不同,问:共有多少种染色方法?
建立对应关系求解问题,在看似没有联系的两类问题之间搭建桥梁,悄然发现许多问题都是殊途同归,万象归一.
2.题型二⇒动点问题
虽然此题在题型一基础上只增加了限制条件“只能把球传给相邻的人”,但在解法上却截然不同,需要重新构造与之对应的模型.
建立对应关系
我们规定传球过程中顺时针传球为正向,逆时针传球为负向,设n次传球中有x次正向传球,n-x次负向传球.
在动点运动问题中有以下题型:一动点从原点出发,在数轴上运动,每次只能向左或向右运动一个单位长度,经过n(n≥3)次运动后,该点所处位置的坐标为m(m∈N∗)的整数倍,问:该点的运动方式共有多少种?
该题型与题型二存在以下对应关系:
(1)A1所在位置相当于数轴原点;
(2)n次传球对应动点的n次运动,顺时针传球一次相当于点向右运动一个单位,逆时针传球一次相当于点向左运动一个单位;
(3)球最后回到A1手中必符合以下三种情形之一:
①正向传球和负向传球的次数一样多;
②正向传球次数比负向传球次数多时,多的次数必为m的正整数倍;
③负向传球次数比正向传球次数多时,多的次数也必为m的正整数倍.
以上三种情形都相当于点到达位置的坐标为km(k∈Z),其中k=0时意为正、负向传球次数一样多;k>0时意为正向传球次数比负向传球次数多,k<0时意为负向传球次数比负向传球次数多.
(4)点的每一种运动方式对于一种传球方式.
问题解答
n次运动后点处位置的坐标为m(m∈N∗)的整数倍,x应满足条件:x-(n-x)=km(k∈Z),即2x-n=km(k∈Z).对于该方程的每一个自然数解x0,对应着点的运动方式有种(向右运动x0次,向左运动n-x0次).故点的运动方式共种,其中
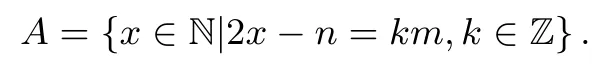
所以,不同传球种数
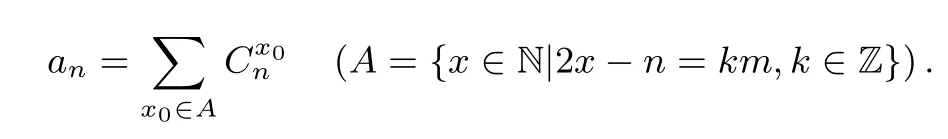
以上解答简洁有效,避免了分类讨论带来的麻烦,可见,通过建立对应关系将原题题设进行等价转换,转换成熟悉的易于理解的题型,是一种重要且有效的解题途径.
另外,还可变化题型背景将题型二改编为青蛙跳动问题.
例2 某青蛙在池塘中的荷叶上跳动,荷叶排列成一圈,青蛙只能在相邻的两片荷叶上跳动,如果池塘中共有10片荷叶,问:青蛙跳14次后恰好回到出发荷叶上的跳动方法.
解 设青蛙顺时针跳动x(0≤x≤14,x∈N)次,逆时针跳动14-x次,则
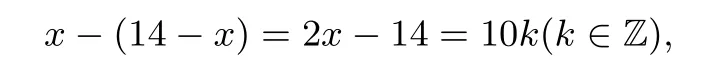
得到x可以取2,7,12.故青蛙跳动方法种数为种.
3.题型三⇒站位问题
题型三中有4次传球,规定每次只能把球传给与自己不相邻的人且每人至多只传一次球,故除A1以外还有3个人传了球,建立对应将此问题转化为“站位问题”.
建立对应关系
如下图
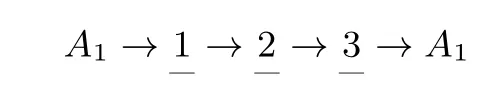
首尾被A1占据,从剩下的m-1个人(A2,A3,...,Am)中选三个人去站1,2,3这三个位置,但要求相邻两个位置上的人在“站位”之前不能相邻.记这三个人为:O1,O2,O3,并假设这三个人的顺序如下:
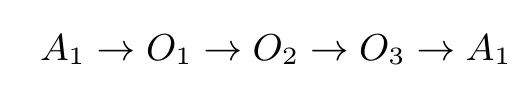
根据题意特殊位置特殊安排,先确定O1,O3,再确定O2.O1,O3“站位”之前的位置关系直接影响了O2的取法,而O1,O3均不能与相邻,O2不与O1,O3相邻.
问题解答
根据O1,O3“站位”之前的位置关系不同,分以下3种情况讨论:
(1)O1,O3相邻.
此时O1,O3有m-4种取法(从除A1以及与A1相邻的两个人以外的m-3个人中选两个相邻的人),满足条件的O2有种m-5取法,故O1,O3相邻时传球方式有种.
(2)O1与O3之间间隔1人.(按较少间隔计)
此时O1,O3有m-5种取法(从除A1以及与A1相邻的两个人以外的m-3个人中选两个人且这两人之间间隔为1人),满足条件的O2有m-6种取法,故O1与O3之间间隔1人时传球方式有:A22(m-5)(m-6)种.
(3)O1与O3之间间隔人数为2人或2人以上.(按较少间隔计)此时O1,O3有
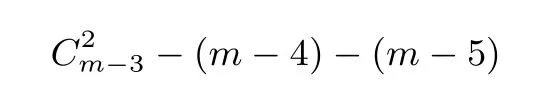
种取法,满足条件的O2有m-7种取法,故O1与O3之间间隔人数为2人或2人以上时传球方式有
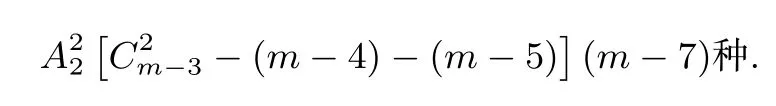
综上,不同传球方式的总数为:
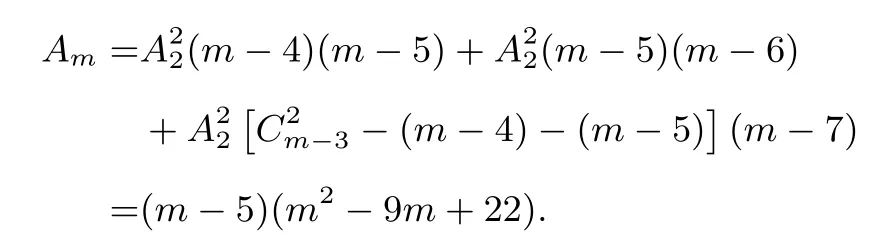
评注 本题笔者是以O1,O3(即第2次传球和第4次传球的两个人)之间的位置关系为分类依据,也可以找到其它的分类标准,但切记做到“分类不重不漏,分步有理有据”.由于规定每次只能把球传给不相邻的人且每人至多只传一次球后情况比较复杂,用初等方法无法建立传球方式的总数关于传球次数的函数关系,故本题把传球次数具体到4次,当然也可以求出传球5次、6次...的传球方式的总数,感兴趣的读者可以继续往下探索.
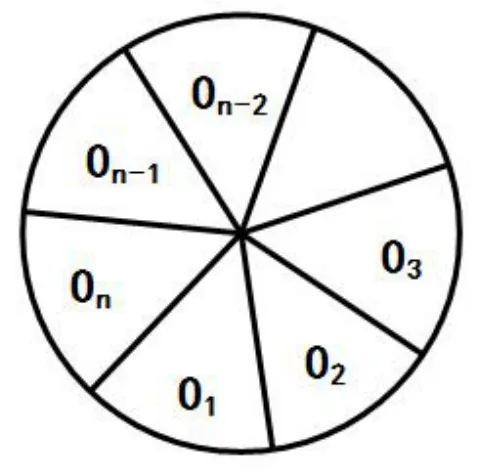
图1
例3 如图3,7个人A1,A2,...,A7围成一圈相互传球,规定每次只能把球传给与自己不相邻的人,且每人至多只传一次球.首先由A1发球作为第一次传球,经过4次传球,球又回到A1手中,试求所有传球方式的种数.
解 由题意可知:除了A1之外还有3个人传了球,设这3个人为O1,O2,O3,且设传球次序为:A1→O1→O2→O3→A1,根据O1,O2,O3这3个人在图3中的位置关系不同,分以下三种情况:
(1)O1,O3相邻.
此时O1,O3可能分别是A3,A4、A4,A5、A5,A6或A4,A3、A5,A4、A6,A5,对于O1,O3的每一种取法,O2都仅有2种可能(例如:O1,O3分别是A3,A4时,O2可能是A6或者A7,其它情况以此类推).故O1,O3相邻时有6×2=12种传球方式.
(2)O1与O3之间间隔1人.(按较少间隔计)
此时O1,O3可能分别是A3,A5、A4,A6或A5,A3、A6,A4,对于O1,O3的每一种取法,O2都仅有1种可能(例如:O1,O3分别是A3,A5时,O2可能是A7,其它情况以此类推).故O1,O3之间间隔1人时有4种传球方式.
(3)不存在O1与O3之间间隔人数为2人或2人以上(按较少间隔计)的情况.
综上,所有传球方式有16种.
4.感悟
美籍匈牙利数学家波利亚说:“如果你不能解决这个提出的问题,环视一下四周,找一个适宜的相关问题,它可能提供解的方法,解的轮廓,或是提供我们应从哪一个方向着手工作等等.”在碰到新的数学问题时,学生一般都会有畏难心理,事实上,难的不是问题本身,而是我们往往被问题的面具吓到.莫为浮云遮望眼,揭开问题表面的面纱,将新的数学问题与已有的知识结构相联系,广泛联想与想象,进行发散思维,通过建立对应关系,将复杂问题简单化、陌生的问题熟悉化、熟悉问题规律化.学会举一反三,横向类比,纵向延伸,这样才能以不变应万变!
[1]罗增儒.从竞赛到高考,从染色到传球[J].中等数学,2006(10):18-22.
[2]徐国君.殊途同归,万象归一—再谈传球问题与染色问题[J].中学数学研究,2011(5):45-46.
[3]G·波利亚.怎样解题[M].北京:科学出版社,1982.
*全国教育科学规划教育部重点课题—TPACK视角下卓越教师培养的理论研究与实践探索(课题编号:DHA150287).

