数列不等式放缩法——由一个自招题谈数列放缩的解题策略

浙江大学附属中学(310021) 陈斌

云南省昆明市寻甸县柯渡镇柯渡中学(655212) 杨彩清

数列不等式放缩法
——由一个自招题谈数列放缩的解题策略

浙江大学附属中学(310021) 陈斌

云南省昆明市寻甸县柯渡镇柯渡中学(655212) 杨彩清

2017年是全国新高考改革的元年,而数列不等式放缩是今年浙江新高考的压轴题和名校自招必考题,所以研究数列不等式放缩问题显得很有必要.目前比较有效的数列不等式有很多,例如：分析通项法、裂项分析法、等比数列法、切线放缩法、二项式放缩法等.其中迭代函数不动点放缩是处理{an}与Sn范围问题非常常用的方法.本文就以今年一道自主招生的数列不等式放缩为例,来详细讲解此方法的奥妙与技巧.

数列不等式放缩 不动点裂项 迭代函数

一、试题呈现

例 (2017年复旦大学自主招生望道计划简答题第2题)已知正项数列{an}满足

(1)求证：当n≥2时,an≥1.

(2)求证：{an}收敛.

二、多维分析 直击要害

思路1(1)一般处理{an}的范围问题,往往最直接的处理方法是直接运用数学归纳法.因为数学归纳法是一种处理与正整数有关的非常有效的一种数学解题方法,但是需要注意的是在使用这方法时必须用假设的条件证明出结论,否则证明是错误的.(2)处理{an}收敛.往往只要证明单调有界即可.

解法1(1)由正项数列{an}满足

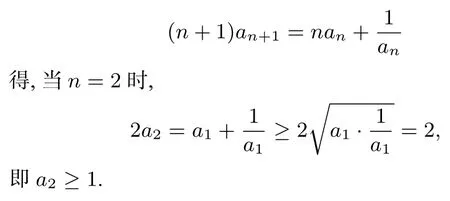
假设当n=k时,ak≥1不等式成立.

当n=k+1时,下证：ak+1≥1.

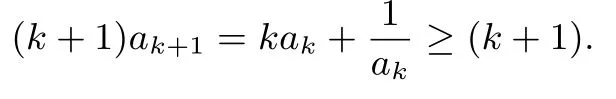
由ak＞0,得,只要证

又由于ak≥1,得(ak-1)(kak-1)≥0不等式成立.

(2)要证明{an}收敛,只要证{an}单调有界即可.由(1),可知an≥1.故只要证明{an}单调递减即可.而要证明{an}单调递减,可以利用{an}作商,即只要证明即可.由于当n≥2时,

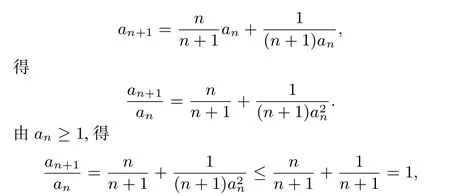
即an+1≤an.此时可知{an}为常数列或单调递减.

①当{an}为常数列时,an=c≥1,数列{an}是收敛的;

2②当{an}为单调递减时,且an≥1,此时{an}是单调递减且有界的,故数列{an}收敛.

思路2一般处理一阶递推数列{an}取值范围问题,往往用迭代函数an+1=f(an).函数迭代法一般需要数学归纳法来解决,而利用数学归纳法就需要对求证的问题进行命题的加强,加强命题时的关键就是需要包含{an}的单调性,那么如何预先知道{an}的单调性就是问题的关键.要预先知道{an}的单调性就需要利用数列的递推函数f(x)的不动点(方程f(x)=x的实数根),求出不动点,画出迭代函数的图像,再借助直线y=x将函数值(也就是a2)“反射”到x轴上,这样就可以比较a1与a2的大小.依次类推就可以猜出数列的单调性与有界性了.

设an+1=f(an),得

令f(x)=x,得

解得x= 1.如图1迭代函数y=f(x),B(1,1)此时由图可猜测：若an≥1,则{an}是单调递减,即an+1＜an.故要证明 当n≥2时,an≥1.可以对此不等式进行命题加强,只要证：当n≥2时,1≤an+1＜an.

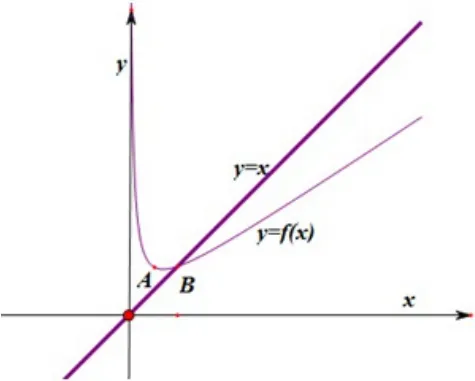
图1

下面利用数学归纳法证明即可.令an+1=f(an),得且当x＞1时,

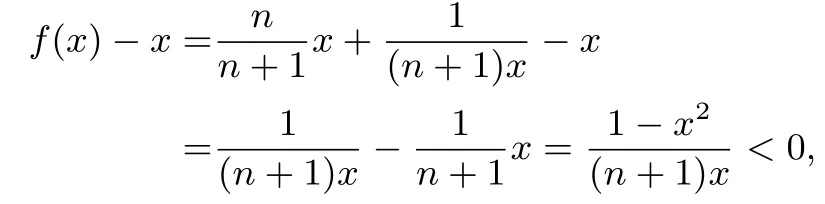
即f(x)＜x.当n=2时,

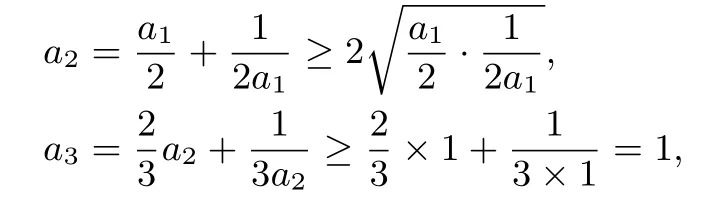
则1≤a3=f(a2)＜a2.假设当n=k时,1≤ak+1＜ak不等式成立.当n=k+1时,由an+1=f(an),得

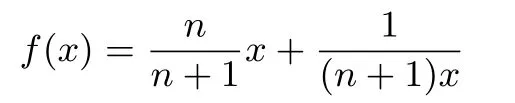
在(1,+∞)上是递增函数.则f(1)≤f(ak+1)＜f(ak),化简可得 1≤ak+2＜ak+1.综上所得当n≥2时, 1≤an+1＜an,即an≥1.

(2)由(1)可得,{an}是单调递减的,且an≥1,故可知{an}是收敛的.

思路3 处理{an}的范围问题,我们经常使用作商法,即前后两项之比的比值与1作比较,但是如果直接使用作商法往往是求不出{an}的范围问题的.一般我们需要先求出迭代函数an+1=f(an),f(x)的不动点x=x0,从而将迭代函数转化为再利用g(an)求出{an}的范围.而且这种方法是处理{an}前n项和{Sn}范围问题的最常用的方法,本文由于篇幅有限,不再详细叙述.

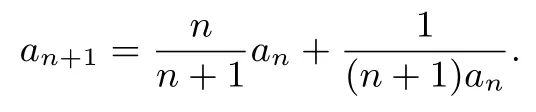
设an+1=f(an),得

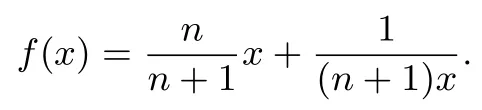
令f(x)=x,得

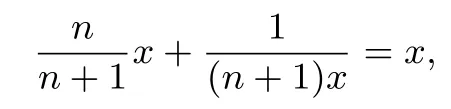
解得x=1.此时

要证明an≥1,只要说明就可以得出an+1-1与an-1同号,故只要说明a2-1≥0即可.又由于

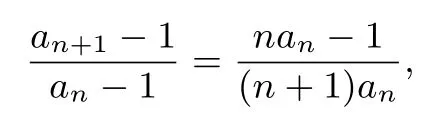
只要证明nan-1＞0即可.

下证：当n≥2时,当n=2时,

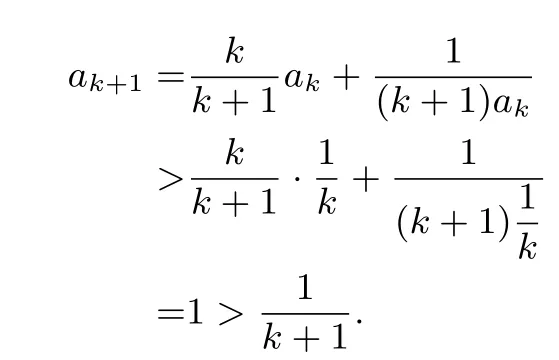
从而可知当n≥2时,此时可知即an+1-1与an-1同号.又由于

可知故当n≥2时,an＞1.

(2)由(1),可得

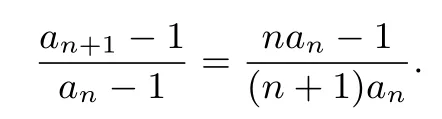
由于{an}是正项数列,得an＞0,此时

又由于当n≥2时,an≥1.可得an+1-1＜an-1,即{an}是单调递减的数列,此时1≤an+1＜an.综上所述{an}是收敛的.

三、反思与拓展

上述解法一直接运用数学归纳法,虽然解题思路非常简单,对学生来说也容易想到,但是它的短板也非常明显,就是对于大多数稍微难点的问题,直接运用数学归纳法是做不出来的,所以一般在高考数列的压轴题、自主招生考试与省竞赛中都不采用这样的方法,更多的时候我们运用解法二,解法二是处理数列放缩的常用方法.

解法二利用迭代函数an+1=f(an),求出y=f(x)不动点,从而根据迭代函数y=f(x)与y=x的图像,对要求证的{an}的范围进行加强命题,加强命题时需要包含{an}的单调性,再结合数学归纳法求证出结论.但有些时候不一定能直接求出.比如此时可以将上式看成以an+1为自变量,求出

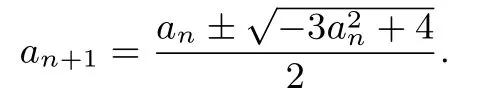
一般这两个有一个是不满足条件的.这时需要再结合题中所给条件,写出适合此题的迭代函数.倘若题中所给条件如果实在求不出迭代函数an+1=f(an),也可以运用an=f(an+1),求证方法与上述类似.解法二这种方法不仅适合求的范围,在处理{an}前n项和{Sn}的范围、压缩数列求和范围、点列求和范围、零点数列求和范围等问题时也非常有效,也是最常用的方法.

这类方法分为五步,也称“五步法”求解递推型问题.

模型：已知数列{an}满足a1=a,an+1=f(an),n∈N∗一般解题步骤如下：

第一步：找出迭代函数：f(x);

第二步： 求出迭代函数的不动点：由f(x)=x,得x=x0;

第三步：“中心化”再作商得到“变比”g(an),研究数列在不动点附近的性质：求出分析g(an).

第四步：计算“变比”在不动点处的函数值并判定类型：

①若|g(an)|=1,则数列为“裂项相消”型.

②若|g(an)|＞1(＜1),则数列为“等比”型,可放缩成等比数列;

第五步：若第四步判定的类型为“裂项相消型”,则对“中心化”式子取倒数、裂项、累加：

①“中心化”取倒数,得到

②裂项成可累加相消结构：

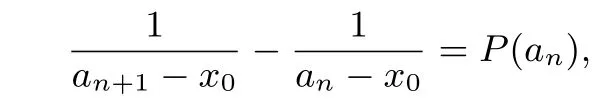
这里的{P(an)}为“伴随”数列.

③累加：得到

从而求出an关于n的不等关系式.

④若结论要证明h(n)＜Sn＜t(n),只要证明

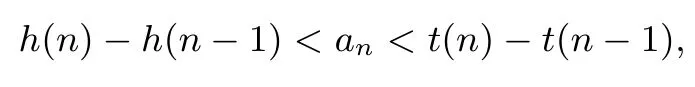
再结合③式就可以求出所要证明的结论.

若第四步判定的类型为“等比型”,则放缩成等比数列：

①分析“变比”

②根据an的范围,确定变比g(an)的范围,即等比数列的公比,再结合伪等比数列进行放缩.

③利用Sn=a1+a2+···+an＜b1+b2+···+bn=(其中q＜1)进行等比放缩.

④此时只要证明an＜bn即可,但是更多的时候需要将数列{an}前两项不进行放缩,从第三项开始伪等比放缩.此时需要根据当n≥3时an的范围,来对“变比”g(an)进行重新放缩.

四．真金冶炼

例题 (2017年温州高三数学第二次调研22题)设数列{an}满足的前n项和,证明 对任意的n∈N+,

(1)当0≤a1≤1时,0≤an≤1;

(2)当a1＞1时,

解析 (1)直接用数学归纳法.

(2)迭代函数f(x)=x2-x+1,由f(x)=x,得不动点x=1.由不动点法可知,1＜an＜an+1.故

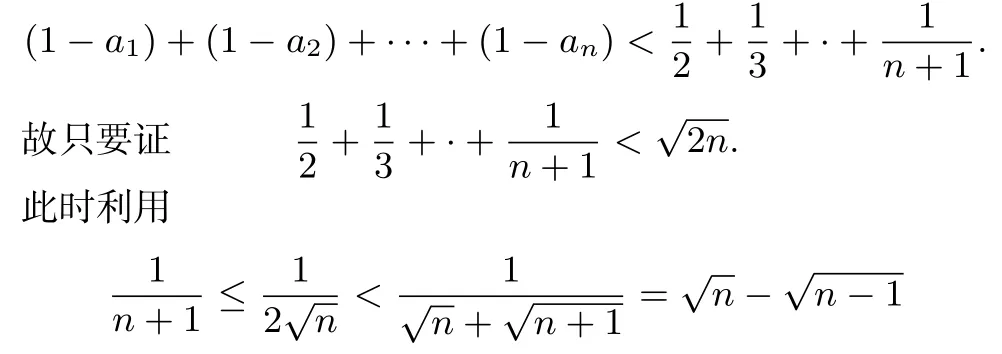
裂项相消即可.

五、回归本质

数列不等式放缩今年在各名校的自主招生中特别火,本质在于级数不等式的处理是高等数学特别重要的一部分,它是初等数学向高等数学跨越的基础.数列不等式放缩的核心是数列的极限思想,而迭代函数与不动点裂项正好是处理数列极限(不动点就是数列的极限)的关键.再加上今年又是新高考改革的元年,命题人对于数列出题的方向已经非常明确,需要我们学生和教师引起足够的重视.