构造函数法在不等式证明中的应用

广东顺德德胜学校528333 唐国秋

构造函数法在不等式证明中的应用

广东顺德德胜学校528333 唐国秋

构造函数法,是导数中的一个非常重要的方法,在导数中应用非常普遍,它很好地把数学中的各种方法联系起来,比如作差法、放缩法、化归法,也渗透着探索、概括、归纳的思想.能不能构造出一个适宜的函数,往往决定着题目能不能顺利解决,也体现学生的基本功是不是很扎实.本人研究近几年的高考试题,总结几类常见的构造函数的技巧,从而提高学生分析,解决问题的能力.

一、利用作差,构造函数

例1证明：当x＞0时,lnx＜x.

评注函数的不等式问题,应用导数工具的策略是：作差构造函数.这种类型一般都是把式子全部移到不等式的一边,构造辅助函数,利用导数工具研究辅助函数的性质、最值进而得证.

变式练习证明：当x∈(0,π)时,sinx＜x.

简析构造函数f(x)=x-sinx,通过f(x)求导,得y=f(x)在x∈(0,π)单调递增,得最小值f(0)=0,得证.

二、分离变量,构造函数

例2已知函数f(x)=xlnx,g(x)=-x2+ax-3.对一切的x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.

解析 ∀x∈(0,+∞),有2xlnx≥-x2+ax-3,则

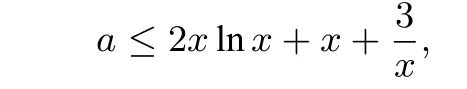
评注 对于一些含有参数的恒成立问题,可以把参数分离出来,然后把不等式的另一边构造辅助函数,利用导数工具研究辅助函数的最值,求解问题.

三、挖掘相似结构,构造函数

例3已知函数f(x)=ex-ax,其中a＞0,函数f(x)的图像上取定点A(x1,f(x1)),B(x2,f(x2)),(x1＜x2),记直线AB的斜率为k.证明：存在x0∈(x1,x2),使f′(x0)=k成立.

证明 由题意知,

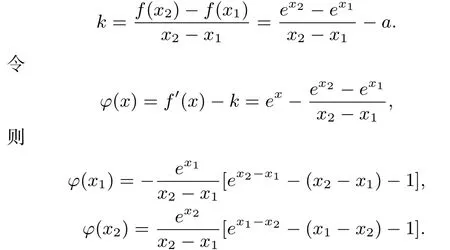
令F(t)=et-t-1,则F′(t)=et-1

当 t＜ 0时,F′(t)＜ 0,F(t)单调递减;当 t＞ 0时,F′(t)＞0,F(t)单调递增.故F(t)＞F(0)=0,即

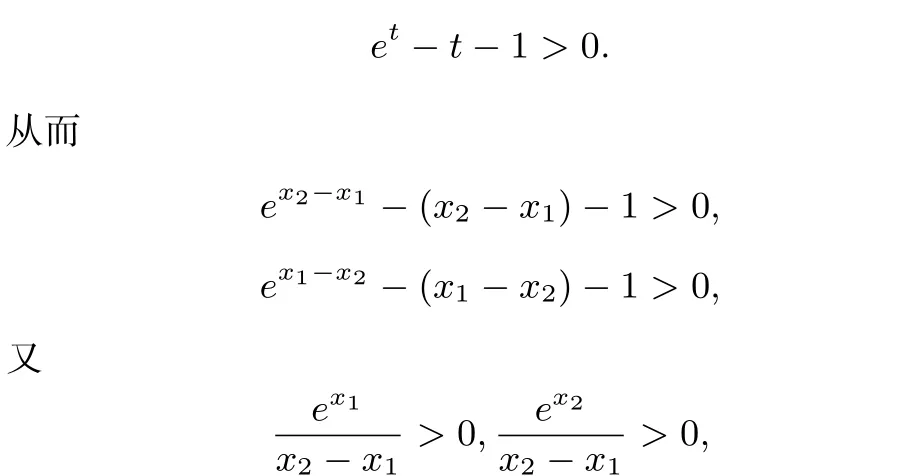
所以φ(x1)＜0,φ(x2)＞0.

因为函数y=φ(x)在区间[x1,x2]上的图像是连续不断的一条曲线,所以存在x0∈(x1,x2)使φ(x0)=0即f′(x0)=k成立.

评注 本题要善于挖掘出(x2-x1),把(x2-x1)看做一个整体t,进而构造辅助函数.这种类型的题往往有多变量,把多变量“凑”成相同的结构,然后把这个结构记为整体,就变成一个变量了.数学中的整体观,大局观在构造函数中很重要.

四、合理放缩,构造函数

(I)求a,b的值.

证明 (I)a=0,b=-1,过程略;

(II)当x＞0时,由均值不等式得

则当0＜x＜2时,

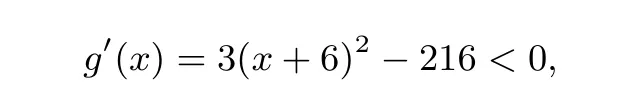
所以 g(x)在 (0,2)内是递减函数,又 g(0)=0,因为h′(x)＜0所以h(x)在(0,2)内是递减函数,又h(0)=0,所以h(x)＜0,所以当

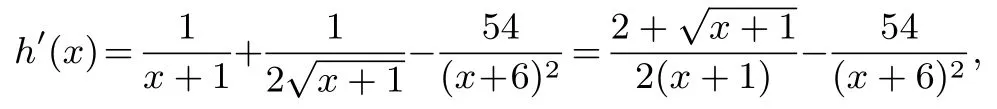
评注 此题导函数比较复杂,直接分析导函数,根本得不到单调区间,需要我们对导函数通过放缩,化简,得到一个适宜的函数,然后才能顺利地求导,得到最值.构造函数法在导数题目中是一个很重要的方法,问题关键是要判断导函数的符号,这是需要时刻清楚的.

对应练习已知a∈R,函数f(x)=4x3-2ax+a,证明：当0≤x≤1时,f(x)+|2-a|＞0.

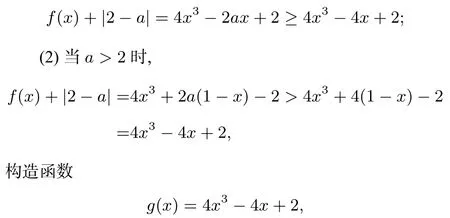
简析(1)当a≤2时,求g′(x),得g(x)＞0,得证.

五、构造“原函数”

例5(2015高考福建,理10)若定义在R上的函数f(x)满足f(0)=-1,其导函数f′(x)满足f′(x)＞k＞1,则下列结论中一定错误的是（）

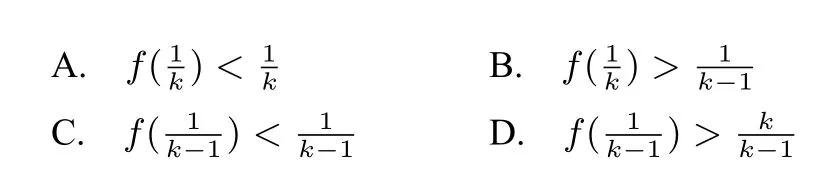
证明 由已知条件,构造函数g(x)=f(x)-kx,则g′(x)=f′(x)-k＞0,故函数g(x)在R上单调递增,且所以进而所以一定错误的是C,选项D无法判断;构造函数h(x)=f(x)-x,则h′(x)=f′(x)-1＞0,所以函数h(x)在R上单调递增,且所以即选项A,B无法判断,故选C.

评注 这些类型题目的特点是条件中有f′(x)这样的式子.本题通过条件中f′(x)＞k＞ 1,构造出原函数g(x)=f(x)-kx和h(x)=f(x)-x,从而h(x),g(x)单调增,再分析得解.构造函数的思维采取了逆推,利用导数形式构造出原函数.

变式练习设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x＞0时,xf′(x)-f(x)＜0,则使得f(x)＞0成立的x的取值范围是( )

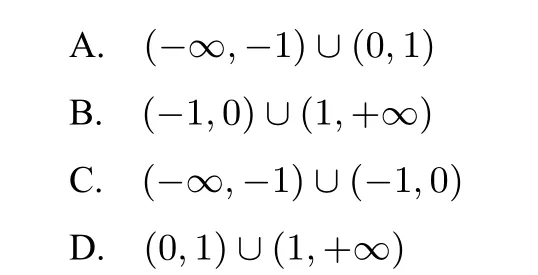
简析构造函数即可.

总之构造函数具有很强的灵活性、创新性、综合性,在解数学题时,需要观察题目条件结构特点,发现条件中的关系,灵活构造出符合题目特点的函数.