一个模考题引出的探究
浙江省宁波市第四中学315016 魏定波
一个模考题引出的探究
浙江省宁波市第四中学315016 魏定波
1 问题呈现
设P椭圆上的动点,F1,F2为椭圆的焦点,I为△PF1F2的内心,则直线IF1和直线IF2的斜率之积( )
A.是定值 B.非定值,但存在最大值
C.非定值,但存在最大值 D.非定值,且不存在最值
这是2017年浙江省温州市高考模拟试题第10题,以椭圆为载体,考查了椭圆几何性质,三角函数和几何变换.在调查中发现,学生普遍反映进入解题情境困难,感觉有劲使不上.本文从问题的解答入手,进行一番探究.
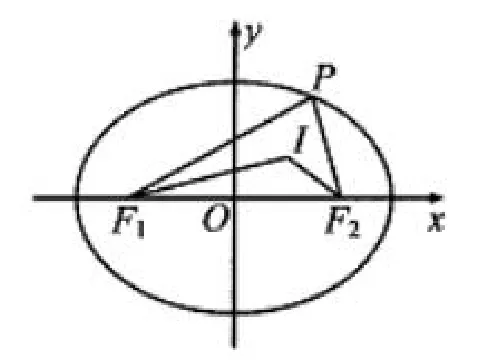
图1
2 问题解答
解法1(借助三角恒等变换)
在△PF1F2中,由正弦定理,得:
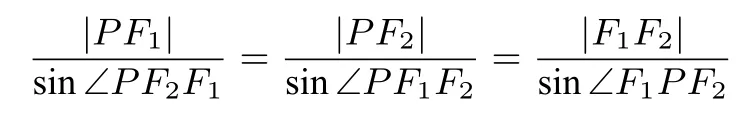
设∠PF1F2=α,∠PF2F1=β,则
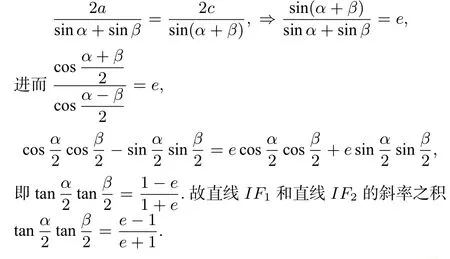
解法2 (借助焦点三角形的旁切圆)如图2,记△PF1F2的一个旁切圆为圆J,容易证明F1,I,J共线,IF2⊥JF2,由圆的切线长定理和椭圆的定义,
可知: 2c+|F2M|=2a-|F2M|,|F2M|=a-c,即切点M就是右顶点A2,所以
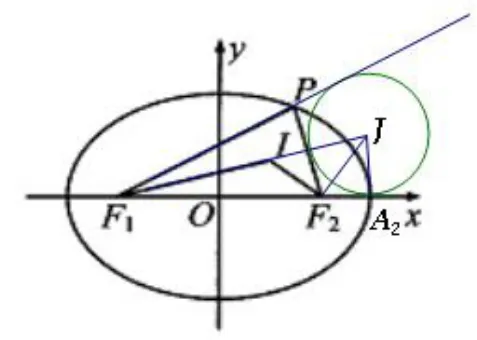
图2
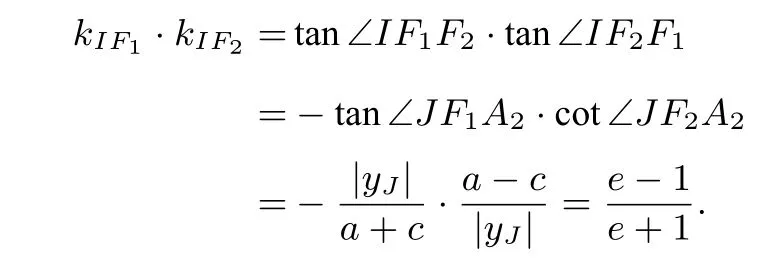
3 问题探究
探究1 三角形内心的轨迹
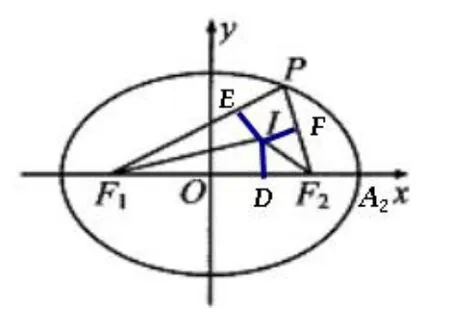
图3
如图3,设点P(x0,y0),内心I为 (x,y),焦点F1(-c,0),F2(c,0),|PF1|=r1,|PF2|=r2,则r2-r1= 2ex0,过内心I作ID,IE,IF分别垂直F1F2,F1P,F2P于点D,E,F.因为点I是△PF1F2的内心,点D,E,F是内切圆的切点,由切线长定理,得方程组
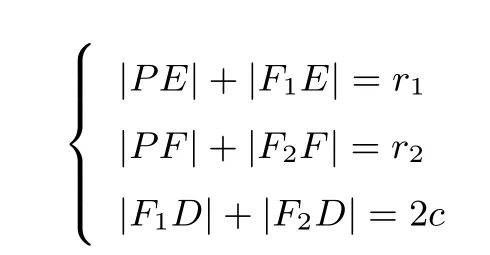
结合r2-r1=2ex0,解得|F1D|=c+ex0,又|F1D|=c+x,得
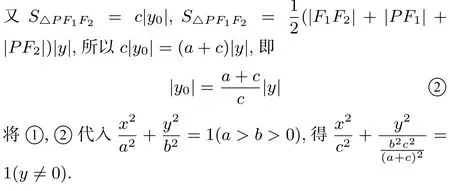
探究2相关结论
我们知道动点I的轨迹是以F1(-c,0),F2(c,0)为长轴顶点短轴长为的椭圆.对于kIF1·kIF2的定值问题,联想到人教版(A版)高中数学选修2-1的P41页例3:设A,B的坐标分别为(-5,0),(5,0),直线AM,BM相交于点M,且它们的斜率之积是求动点M的轨迹方程,并判断轨迹的形状.
由此,我们还可得到如下结论:
结论1平面内到两个定点A1(-a,0),A2(a,0)的斜率之积等于的点的轨迹是以BC为长轴的椭圆
结论3设A,B是过椭圆中心的任意一条弦的两个端,点P为椭圆上任意一点,则
证明 设点P(x0,y0),则
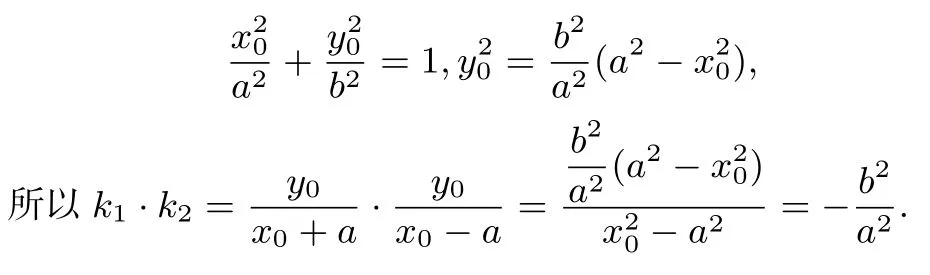
结论4 设直线L与椭圆交于A,B两点,C为线段AB中点,则
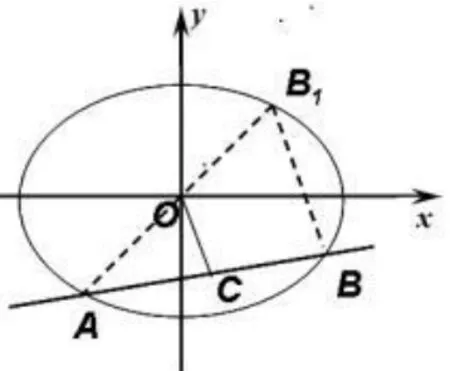
图4
证明 如图 4,连延长AO交椭圆于B1,则OC//BB1,则
此式如果与直线和圆的位置关系进行类比,我们称它为椭圆的“垂径定理”.
4 连线考题
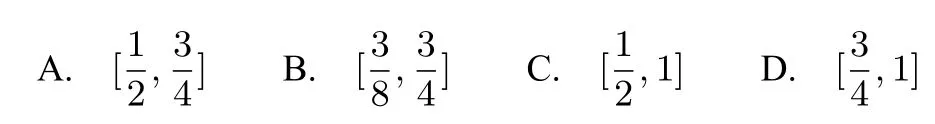
由kPA2∈[-2,-1],得故选B.
例2(湖北省武汉市2017届高中毕业生五月模拟考试数学(理)试题第12题)已知椭圆内有一点M(2,1),过M的两条直线l1,l2分别与椭圆E交于A,C和B,D两点,且满足
(其中λ>0,且λ/=1),若λ变化时,AB的斜率总为则椭圆E的离心率为()
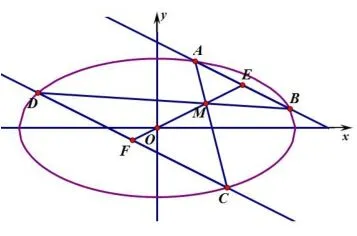
图5
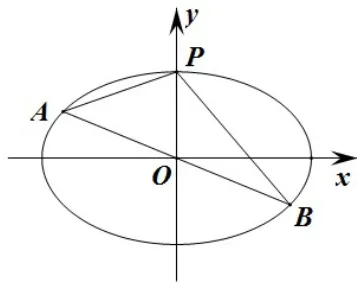
图6
解析 设A(x0,y0),则B(-x0,-y0),则
若设直线PA斜率为k,则直线PB的方程与联系,得

PB中点所以PB中垂线方程:得yN=在椭圆内部,所以
(1)求椭圆E的方程;
(2)设不过原点O且斜率为的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D.证明:|MA|·|MB|=|MC|·|MD|.
(2)设直线l的方程为A(x1,y1),B(x2,y2).由于于是直线lOM的方程为可得M点坐标为由方程组得
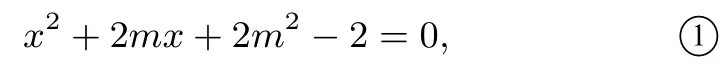
方程 1的判别式为△=4(2-m2),由△>0,即2-m2>0,解得由 1得
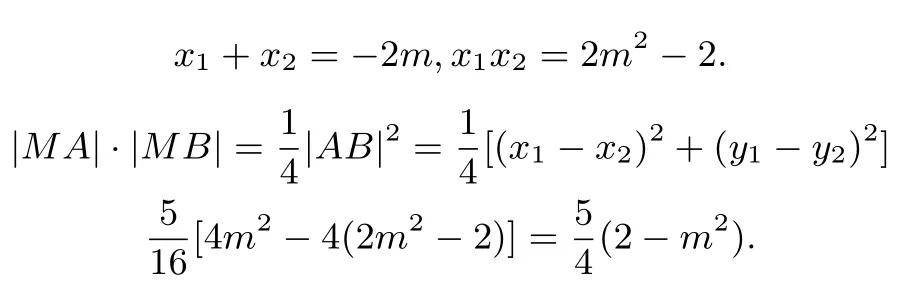
所以
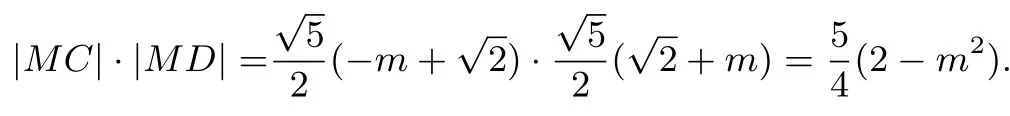
故|MA|·|MB|=|MC|·|MD|.
回头梳理整个定值问题的探究及运用过程,最大的感触就是不要轻易“放过”教材中任何一道题目,教材是专家经验的积累、智慧的结晶,所以每道例题、习题都有其存在的价值,作为一线的教师要学会引领学生做好深度研究,教会学生利用好教材,教会学生如何对一道题目进行探究更是必要的,其过程足以让学生拥有充足的知识储备,它会让学生找到简单有效的方法应对高考中的难题,并从中获得快乐、激发潜能,提高学习兴趣.

