可补形为长方体计算的棱锥外接球问题
河南省洛阳市河南科技大学附属高级中学(471003) 李昭辉
河南省洛阳市洛阳理工学院数学与物理教学部(471023) 童新安
可补形为长方体计算的棱锥外接球问题
河南省洛阳市河南科技大学附属高级中学(471003) 李昭辉
河南省洛阳市洛阳理工学院数学与物理教学部(471023) 童新安
近年来,棱锥的外接球问题作为高考的热点问题,对学生的空间想象能力和逻辑分析能力提出了较高要求.而《普通高中数学课程标准(实验)》中指出[1]:“在立体几何初步部分,学生将先从对空间几何体的整体观察入手,认识空间图形;再以长方体为载体,直观认识和理解空间点、线、面的位置关系......”.所以在求解棱锥的外接球问题时,如果能发现棱锥满足的某些特征,将其补形成长方体再进行计算,则往往能达到事半功倍的效果.本文介绍了几种常见的能补形为长方体计算的棱锥外接球模型,并给出了示例.
一、长方体的外接球模型
定理 已知长方体ABCDA1B1C1D1,记其长AB=a,宽AD=b,高AA1=c,则其外接球的球心位于该长方体对角线的中心O处,如图1所示;其外接球的半径为
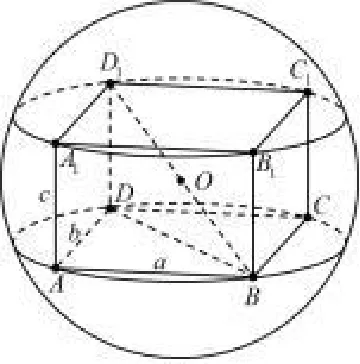
图1
证明长方体的体对角线交于中点O处,由对称性可知,O点到各顶点的距离相等,则O即外接球的球心;由勾股定理,在Rt△ABD中,AB=a,AD=b,所以所以故其外接球的半径为r=
二、可补形为长方体计算的棱锥外接球模型
模型1“三垂直”模型
如图2.1所示,若三菱锥D-ABC满足DA⊥平面ABC,∠BAC=90◦,AB=a,AC=b,AD=c,则该三菱锥的外接球的半径为
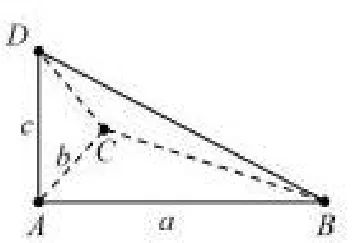
图2.1

图2.2
分析该三棱锥的特点为一顶点A处的三条棱AB、AC、AD两两互相垂直.可简记该模型为“三垂直”.将该三棱锥补形为以该三条棱分别为长、宽、高的长方体,如图2.2所示.则由上述定理可知,该三棱锥外接球的半径为
例 1 (2017年广元模拟)如图 3.1,边长为 2的正方形ABCD中,点E、F分别是AB、BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A、B、C三点重合于点A′,如图3.2.若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为___
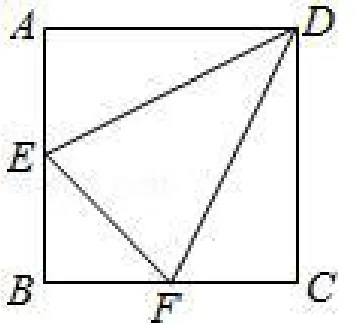
图3.1
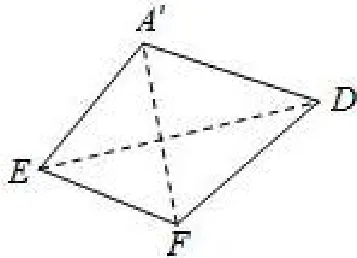
图3.2
解 四面体A′EFD中,在A′点处的三条棱A′E、A′F、A′D两两互相垂直,符合“三垂直”模型特征,又A′E=A′F=1,A′D=2,故该三棱锥外接球的半径为

对模型1作适当扩展,可得如下推论1.
推论1如图4.1所示,若四棱锥P-ABCD满足PA⊥平面ABCD,平面ABCD为矩形,AB=a,AD_=b,AP=c,则该三棱锥的外接球的半径为

图4.1

图4.2
分析该四棱锥的底面矩形ABCD可看作补形而成.由模型1可知,该四棱锥仍可补形为如图4.2所示的长方体,则其外接球半径为
例2(2017年重庆模拟)某几何体的三视图如图5.1所示,则该几何体的外接球的表面积为( )
A.24πB.12πC.8πD.6π

图5.1

图5.2
解 画出该几何体的直观图如图5.2所示,底面ABCD为边长为1的正方形,侧棱PA⊥底面ABCD,PA=2.根据推论1,该四棱锥可补形为以AB、AD、AP分别为长、宽、高的长方体,所以其外接球半径为其外接球表面积为S表=4πr2=6π,答案选D.

模型2“直角+垂”模型
如图6.1所示,若三棱锥D-ABC满足DC⊥平面ABC,∠BAC=90◦,AB=a,AC=b,CD=c,则该三棱锥的外接球的半径为

图6.1
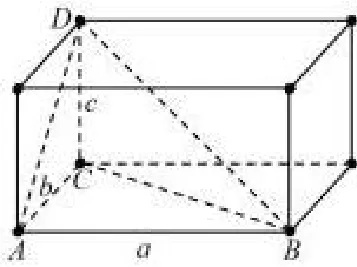
图6.2
分析 该三棱锥的特点为底面三角形ABC为一直角三角形,在其非直角顶点C处有一条棱CD⊥底面ABC.可简记该模型为“直角+垂”.可将该三棱锥补形为以底面ABC的两条直角边AB、AC和垂线CD分别为长、宽、高的长方体,如图6.2所示.则由上述定理可知,该三棱锥的外接球的半径为
例 3(2008年浙江卷)如图 7,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=则球O的体积等于___

图7
解 该三棱锥中,AB⊥BC,故底面三角形ABC为直角三角形,
在其非直角顶点A处有一条棱DA⊥底面ABC.根据前述“直角+垂”模型,则可将其补形为以DA、AB、BC为边长的长方体.故外接球半径所以外接球的体积
对模型2作适当扩展,可得如下推论2.
推论2如图8.1所示,若四棱锥A-BCDE满足矩形BCDE⊥平面ABC,在△ABC中,∠BAC=90◦,AB=a,AC=b,CD=c,则该四棱锥的外接球的半径为

图8.1
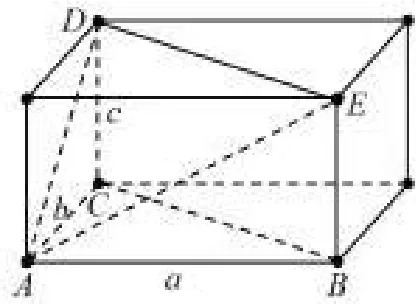
图8.2
分析 该四棱锥的侧面矩形BCDE可看作Rt△BCD补形而成.由模型2可知,该四棱锥仍可补形为如图8.2所示的长方体,则其外接球半径为
例 4 (2016年河南模拟)如图 9,已知四棱锥P-ABCD的底面为矩形,平面PAD⊥平面ABCD,AD=2,则四棱锥P-ABCD的外接球的表面积为()
A.2πB.4πC.8πD.12π

图9

其外接球表面积为S表=4πr2=12π,答案选D.
模型 3“对相等”模型如图 10.1所示,若三棱锥A-BCD满足AB=CD=m,AC=BD=n,AD=BC=p,则该三棱锥的外接球的半径为r=
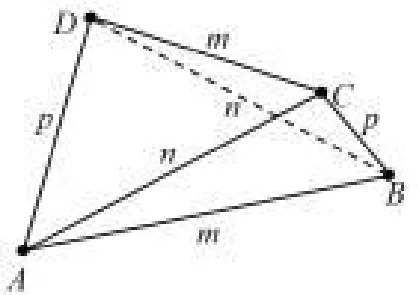
图10.1

图10.2
分析 该三棱锥的特点为三组相对的棱AB与CD、AC与BD、AD与BD分别相等.可简记该模型为“对相等”.可将该三棱锥补形为如图10.2所示的长方体,其中三组相对的棱分别位于长方体的六个面的面对角线上.若仍记长方体的长、宽、高分别为a、b、c,则由勾股定理可知,

所以其外接球半径

例5(2017年郑州三模)四面体A-BCD中,AB=则四面体A-BCD外接球的表面积为()
A.50πB.100πC.200πD.300π
解 很明显,该四面体满足“对相等”模型特征.记

若在模型3中,令三棱锥的边长都相等,可得如下:
推论3 若正四面体的边长为a,则其外接球半径为
分析 正四面体的所有边长均相等,故在模型3中,取m=n=p=a,则其外接球半径为的四面体的四个顶点在同一球面上,则此球的表面积为( )

A.3πB.4πC.D.6π
例6(2003年全国卷)棱长都为
[1]中华人民共和国教育部制订.普通高中数学课程标准(实验)[M].人民教育出版社,2003.

