小学生作图分析数学问题的自觉性研究

崔文闰

摘 要：在小学数学教学中，运用画图和列表分析解决数学问题是图式表征的一种外在表现形式。图式表征对解题有促进作用。本研究采用测试与访谈的方法，利用实验数据分析当前小学生数学解题过程的表征类型，以及影响学生作图分析自觉性的因素，提出具有针对性的教学建议，从而帮助学生学会更好地在多元表征的前提下发挥图式表征思考的作用。

关键词：图式表征；作图分析；自觉性；数学解题；思考问题

一、问题的提出

在小学数学教学中，运用画图和列表分析解决数学问题就是图式表征的一种外在表现形式。能够发挥图表的积极作用，利用作图来思考数学问题是一种能力，而自觉地运用这种能力则是一种思考的习惯，或者说是一种自觉性。这种自觉性有可能成为学生数学学习成长中的一种良好的素养。

那么，当前小学生作图分析数学问题的自觉性如何呢？他们是否具备一定的作图分析能力？对学生自觉作图思考产生影响的因素有哪些？教师如何处理好教学中这些因素的作用，使学生形成良好的数学思考习惯？这些正是本研究所聚焦的问题。

二、研究方法

1. 被试

从某小学选取三、四年级各3个班级，每个班40-50人，作为数学测验施测的对象，并请数学教师根据学生平时的成绩在各班选出优、中、差学生各2名，两个年级共36名学生作为个别访谈的对象。

2. 研究材料

根据学生的数学水平编制数学测试卷，涉及非视觉化题目（NVP：nonvisual problem）与视觉化题目（VP：visual problem），有方位问题、行程问题、植树问题和集合问题等。

3. 研究程序

（1）数学测试

学生以班级为单位在一节课里完成数学测验。教师在三年级的三个班中言语提示程度如下：三（1）班教师不进行任何提示，发卷即做；三（2）班教师在测试前会提醒该班学生可以使用不同的方法答题，包括：列式、言语分析（非视觉空间表征）、画图（视觉空间表征）等；三（3）班教师不仅对学生做出了如三（2）班的言语提示，还利用简易的例子向学生介绍作图分析数学问题的好处和方法。四年级三个班的学生在测试时，教师操作如同三年级。

（2）学生访谈

对选定的36名学生进行个别访谈，每个学生的访谈时间大约为5分钟。访谈时，让学生看着已经做过的试卷向教师解释解题思路。然后教师根据草稿纸的内容与学生的口头叙述，再次确定学生的表征类型。

（3）计分方法

卷面上每一道题目计算方法正确记1分。（对于计算错误的情况予以忽略）卷面分析过程使用了图式表征（例如能够呈现出问题本质的结构性图表）记1分。画出没有关系的图象不得分。由于之前有学者已研究得出图象表征与成功解决数学问题之间呈负相关，故本研究分析不重复该点。

三、分析与讨论

1. 图式表征运用与成功解题的相关性

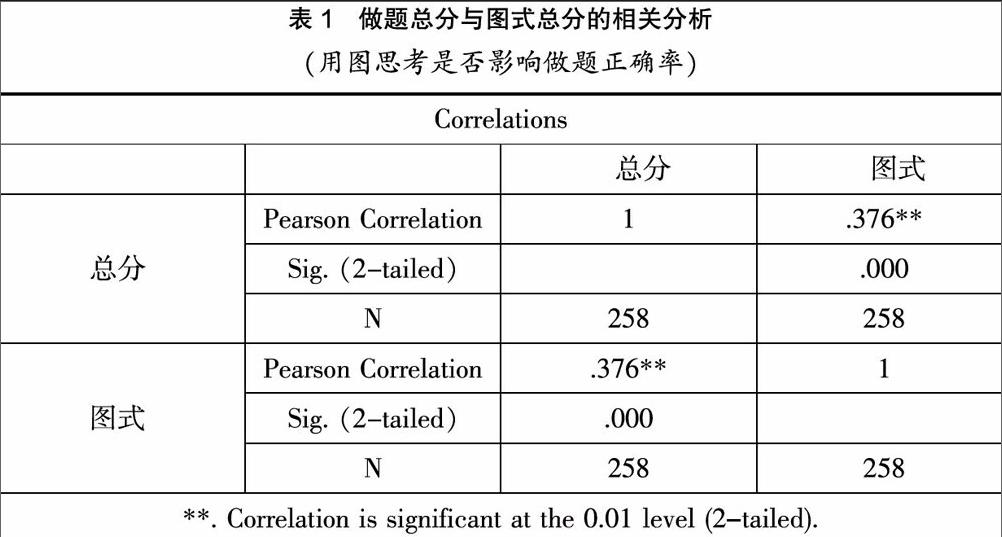
在实验设计中，学生具有结构性图表的思考每题记1分，成功解题记1分，利用spss16.0软件计算两者的相关性（见表1）。

从表1看出，做题总分与图式总分相关系数为 .376** ，Sig. （2-tailed）= .000<.05，是显著相关。即用图思考是影响做题正确率的。这与文献调查中很多学者的研究一致，适当地运用图式表征思考可以促进成功解题。

2. 图式表征运用的程度

通过实验从数据中获知，小学三、四年级的学生运用图表分析数学问题的比率整体约在50%。也就是说，学生在思考过程中能够运用多种表征协助数学思考，其中有一半使用了作圖思考（见表2）。

3. 对学生自觉作图思考产生影响的因素

根据实验设计的情况，再结合实验数据的结果，不难得出对学生自觉作图思考产生影响的因素有以下几点：

（1）教师言语提示与学生思考的成熟度

根据实验设计，（1）班教师对学生是不作任何提示的；（2）班教师在测试前会提醒该班学生可以使用不同的方法答题；（3）班教师不仅提醒了学生可以使用多种方法答题，还利用简易的例子向学生介绍作图分析数学问题的好处和方法。由此看来，三个班的学生在教师不同的言语影响下，答题思考的策略肯定有所不同。那么影响程度如何呢？我们对各班学生运用画图思考的程度做了相关性分析（见表3）。

由表2、表3可见，教师言语提示对学生画图分析的自觉性是有一定影响的，特别是稍低年级的学生尤为明显，很多时候他们的表现是不知道如何表达。当学生思考成熟度增加到一定程度时，他们使用图表思考的自觉性会增加，即便教师没有提示，也会选择多种方法进行数学思考。

但是很明显的是，关于画图思考的指导，短时教授对学生的作用并不大。原因有两个：一是实验中教师的短时教授质量不高；第二个原因，画图思考是一种需要学生自己在较长时间内体验其成功所形成的经验，短时教授需要较高的教学水平，否则效果自然不明显。

（2）数学问题的类型

从表2可以看到，前三题学生使用图表分析的比率是比较大的，而第四题的比率明显很低。另外，关于四道数学题，图式表征运用得分与成功解题得分的相关性显示：前三题的画图分析与成功解题密切相关，第四题的画图分析与成功解题无关（见表4）。

从表4分析画图思考与成功答题（得分）的相关性，第一、二、三题的画图分析与成功答题都是显著相关；而第四题相关系数为 .070 ，Sig. （2-tailed）= .261>.05，是显著相关的。

由此看出，涉及方位问题的数学问题，如地点坐标、植树问题等，用图的适切性较大，学生画图分析的自觉性自然较高。

第四题的数量关系式是关于集合问题的，利用子集与全集的关系得出结论。在访谈中我们了解到，较多解题成功的学生利用子集间的关系直接加减运算即得到结果，认为不需要画图分析。而对于解答集合问题常用的“维恩图”，学生也没有接触过，所以没有使用。endprint

总结得出，数量关系简洁明确的数学问题，学生会直接利用数量关系分析得出结果，这类问题使用图表分析的适切性不大，学生画图分析的自觉性自然也较低。

四、教学启示

1. 学生需要在教师的提示中开拓思维

从学生的心理分析，较小年龄学生在做题的时候，首先想到的是自己曾经获得成功的解题方法，或者是课堂上教师指导过、同学们展示过的解题技巧。有些时候他们的表现是不知道如何表达。如果教师在日常的教学中没有注意使用多种表征（包括言语、图表、符号等）与学生进行学习交流，那么学生在独立思考的时候就会受到单一表征的桎梏。因此，要开拓学生的思维，教师就要使用多元表征与学生进行学习交流，启发学生利用多种途径进行思考是十分必要的。

2. 良好的思考方式需要长期培养

实验发现，短暂的画图指导对学生几乎不起作用。我们指导学生学会自觉运用画图的方法思考数学问题，可以从两方面入手：一是提高短时教授的质量；二是帮助学生在平时就养成良好的画图思考的习惯。前者需要讲求教学方法，当然好的教学方法可以让学生尽快掌握一门绝招。例如，有教师提出“反向引导策略”，即先让孩子学会看图说意，再教会学生据意画图。因为这是双向的，也可以说是表征的转化。多元表征的转化就是对信息的不同处理方式，这是数学思维过程的一种优化训练。对画图思考习惯的培养，是对孩子潜移默化的影响，让学生在日常的学习中发现画图分析的优势，学会如何画图理解数学概念、规律，如何畫图表解答数学问题，更要辩证地运用各种方法，而不是一概而论。

3. 选择恰当的表征类型

各种表征有其特有的优势，一般情况下，问题形式决定了人们常用的表征形式。只有当常规的表征形式不便于或不利于解决问题时，有经验的问题解决者才会采用另一种更有效的表征形式。何为常规表征与更为有效的表征？这取决于学习者成功解题的经验。教师有意识地勤于指导和提示学生采用不同形式的表征策略进行解题，从而获得成功经验，是非常重要的。

能否成功地选择和建构一种适当的表征形式取决于解决问题的综合知识与以往运用某种表征的经验。前者受数学知识习得的影响，后者则可以通过教师对学生进行相关的训练获得经验。学生要学会依据不同问题的数量关系及呈现形式选择恰当的表征类型对问题进行分析，教师就需要在平时训练学生一题多解。比较在同一问题情境下或者同一数量关系下，多元表征各自的优势所在，从而获得辨别的经验。endprint