选准参量 以“动”致“定”*
——评2017年北京市数学高考文科试题第19题
●
(中国人民大学附属中学分校,北京 海淀 100086)
选准参量以“动”致“定”*
——评2017年北京市数学高考文科试题第19题
●唐庚
(中国人民大学附属中学分校,北京 海淀 100086)
圆锥曲线是由运动的点形成的,解析几何就是用代数的方法研究几何问题. 高考试题一般都有“背景复杂、内容丰富、方法灵活、运算量大”的特点. 文章就一类定值问题提供常见思路与解决方案.
定值; 参量; 转化
解析几何问题因其内容丰富——既包含对几何图形的认识和几何量的处理,又有较复杂的代数运算,并且切入点多种多样,与函数、向量、三角函数等有交叉.无论是图形的处理还是代数关系的转化,路径与方法都很灵活,因此解析几何一直是高中数学学习、备考中的重点与难点之一.高考试题一般以常规图形(如线段的垂直平分线、三角形、菱形等)、常规量(长度、面积、角度等)为背景,突破惯性思维,创新设计,倡导学生多观察、多尝试,并运用其内在规律,优化和精确运算.下面结合2017年北京市数学高考文科试题第19题对一类定值问题进行分析与探讨.
1 试题呈现
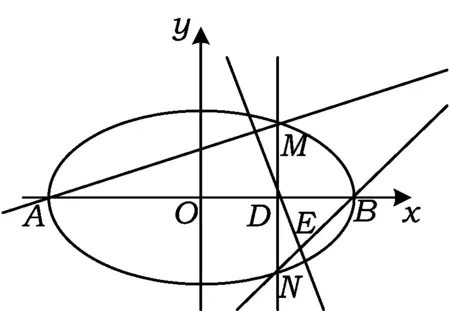
图1
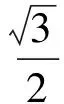
1)求椭圆C的方程.
2)D为x轴上一点,过点D作x轴的垂线交椭圆C于两个不同的点M,N,过点D作AM的垂线交BN于点E.求证:△BDE与△BDN的面积之比为4∶5.
分析1)设椭圆的方程为
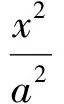
由题意得

2)证明两个三角形面积之比为4∶5,显然是一个定值问题.“定”对应的是“动”,运动中的定值问题本质是寻求运动变化过程中的不变性.本题中运动的始作俑者是“过点D作x轴的垂线”,我们将引入什么样的参量刻画这条运动的直线呢,一个还是多个?又如何用所设的参量建立已知量与所求量之间的关系(即面积之比该如何表达)?参量的变化如何一步步影响所求量?最终结果是一个定值说明面积之比,表达式的某个系数或者整体结构应当满足一定的条件,这个条件是什么?如果是多个变量,那么它们之间又有怎样的联系?能否顺利转化、消减?这是我们要面对的一系列问题.
2 解法探究
笔者认为解决本题中这些问题主要有以下两种方法.
方法1纵观整个问题,所有的变化皆因x轴上的点D的运动而产生,而点D的运动,改变的仅仅是其横坐标.因此,可设D(m,0),M(m,n),并以m,n为参量,依次表示已知条件以及所求面积之比的表达式,再观察,伺机化简.
解法1设D(m,0),依题意知m≠±2,并设M(m,n),N(m,-n),其中n≠0,则直线AM的斜率为
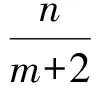
于是直线DE的斜率为
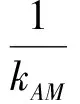
进而直线DE的方程为
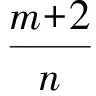
又因为直线BN的方程为
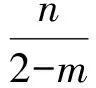
联立
解得点E的纵坐标为
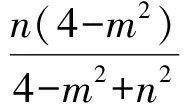
由点M在椭圆C上,知
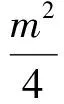
即
4-m2=4n2,
从而
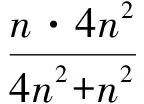
又
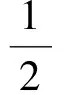
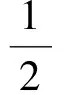
故△BDE与△BDN的面积之比为4∶5.
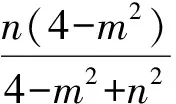
方法2如果我们适当调整变化的先后顺序,将问题转化为:“从左顶点A引直线AM交椭圆于M,过点M作x轴的垂线,交x轴于点D,交椭圆于另一点N,……”,则视角会发生变化.
解法2设直线AM的斜率为k,显然k≠0,则直线AM的方程为
y=k(x+2).
设点M(x1,y1),联立方程组
消去y,可得
(4k2+1)x2+16k2x+16k2-4=0,
显然Δ=256k4-4(4k2+1)(16k2-4)=16>0,
从而
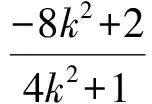
于是直线BN的斜率为
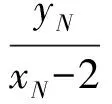
联立直线DE与BN的方程,得
即
两式相减,可得交点E的纵坐标为
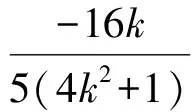
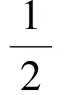
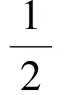
故△BDE与△BDN的面积之比为4∶5.
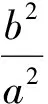
通过以上两种方法的分析可以看出,解决这类定值问题:第一步是引入恰当的参变量(通常有点的坐标、直线的斜率、截距、夹角等);第二步是将几何条件代数化,用参量来表示已知或所求,建立参量与其他量之间等量或不等量的关系式;第三步是化简,利用推理、运算、代数恒等变形等方式进行整理化简,最终消去参量,获得定值.
解析几何把数学的两个基本对象——形和数有机地联系起来,这使得坐标法的作用更加明显,对于人们发现新结论也具有重大意义.除了将“形”翻译为“数”和将“数”翻译为“形”这两个环节外,还有一个关键环节就是代数运算,有时候计算确实繁琐,但是,科研无坦途.北京版《考试说明》对学生的个性品质要求有如此表述:“考生要以平和的心态参加考试,合理支配考试时间,以实事求是的科学态度解答试题,树立战胜困难的信心,体现锲而不舍的精神.”[1]可见具有复杂背景与运算的问题,担负着锻炼、提高学生的意志品质的教育功能.
过去很长一段时间,我们一直在考查“直线与圆锥曲线的位置关系”,以及由此产生的几何元素代数化处理,有的问题解决被程序化、模式化.部分学生一味机械模仿、套用,并没有理解到解析几何是用来刻画运动的点这一本质属性.直线与圆锥曲线相交,研究的是它们产生的这两个交点的相关性质,显然有一定的局限性,既不如一个点在曲线上运动更能体现曲线的定义特征,也不如多点在曲线上自由运动能够带来更加丰富多彩的变化.这几年的高考试题,正逐渐远离传统的以联立为主的命题思路,转而考查一点或者多点在曲线上运动.从这点上说,方法1无疑是我们所倡导的.
[1] 北京教育考试院.2017年普通高等学校招生全国统一考试北京卷考试说明理科[M].北京:开明出版社,2016.
2017-08-01
唐 庚(1971-),男,北京海淀人,中学高级教师.研究方向:数学教育.
O123. 1
A
1003 - 6407(2017)11-45-03

