回归教材寻题根 深度学习悟本质*——一堂高三试题探究活动课的实录与思考

●

(灌南县第二中学，江苏 连云港 222500)

回归教材寻题根深度学习悟本质*
——一堂高三试题探究活动课的实录与思考

●任卫兵

(灌南县第二中学，江苏 连云港 222500)

文章通过一道高三模拟试题的讲评，引导学生在复习迎考的过程中重视“回归教材，寻找题根”． 遇到与教材典型例题、习题有关，而又思路不畅的问题时，应及时翻出教材，寻找类似例习题中所蕴涵的丰富的数学思想和方法． 通过回归教材进行内源性地深度学习，感悟数学本质，提升数学素养．

试卷讲评; 回归教材; 深度学习; 数学素养

0 引言

试卷讲评是高三数学复习教学中的一个重要组成部分.它不仅可以检查学生对所学知识的结构的掌握是否完善，分析问题、解决问题、计算能力是否过关，也能发现教师本身在教学中的不足之处，进行自我反思，不断改进教学策略[1].笔者在多年的教学实践中发现试卷讲评课容易出现以下3个问题：

1)忽视学生的主体性.有些教师在讲评课前，忽视学生的课前自我订正和自我反思；讲评课时，教师从头讲到尾，缺少学生的交流与展示，忽视了学生是学习的主体.

2)讲评缺乏针对性.有些教师在讲评课前既不作学生答题情况的统计，也不作错误原因根源的分析.试卷讲评时，学生没搞清的问题一点而过，不需要多讲的地方却花很多的时间，学生只是在机械地记答案，缺乏激情，这样浪费了学生的学习时间也挫伤了学习积极性，收益甚微.

3)缺少方法指导与思维提升.有些教师在讲评课上只是将正确的答案或解法告诉学生，却没有告知学生应从哪几方面进行解题思路的分析、用什么样的思维去思考，更谈不上挖掘试题的根与源、概括题目背后的数学思想方法.

怎样才能提升试卷讲评课的复习效果呢？笔者一直进行着尝试与思考，结合近日的一次模拟考试试题讲评课，整理成文，与同行交流，不当之处敬请指正.

1 课前准备

(2017年5月江苏省苏锡常镇4市高三数学第3次模拟考试第14题)

通过阅卷反馈，本题学生的得分率非常低，48人参加考试，只有1人得分.为了了解学生对本题的主观认识、解题中的思考过程、学生的失分根源，笔者与学生进行了一次课前谈话，分配了学习小组并布置了相关任务：

1)如果这道题目你做出来了，请你还原考试时的解题过程，并谈谈自己的想法；

2)如果你在解题过程中遇到障碍，请从教材中找一个曾经解决过的类似的题目，并尝试解决障碍.

2 课堂实录

师：同学们，模拟试卷第14题我们班的得分率非常低，只有1位同学做对了.下面先请这位做对的同学说一说解题思路.

生1：我是猜的.

师：能猜出正确答案也是一种本事，能说说你是怎么猜的吗？

师：生1是通过“a与2b的轮换对称性”直觉猜测当a=2b时，目标取到最小值.直觉思维体现的也是一种数学素养.但是猜想有可能出现错误，我们可以尝试用其他方法来验证生1的猜测吗？哪位同学有不同的想法？

得

即

ab≥8，

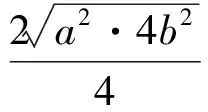
当且仅当ab=8，即a=4,b=2时，上述不等式取到等号.

生3：受生2思路的启发，可以先求a+2b的范围,具体解法如下(思路3)：

师：生2、生3都是通过对已知条件进行变形，得到ab=a+2b，在教材中寻找到它的“根”，运用基本不等式求出ab或a+2b的取值范围，再利用基本不等式或者二次函数求得目标式子的最小值.当我们遇到难以解决的问题时，“寻根”很重要.

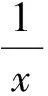
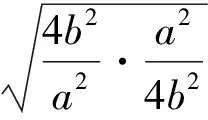
当且仅当a=2b，即a=4,b=2时，取到等号.

生5：生4的思路4可以改进(思路5)：

当且仅当a=2b，即a=4,b=2时，取到等号.

师：很好！生4和生5找到了本题的第二个“根”，考虑“1的代换”，但是怎么想到“分式乘以12”的呢？

生5：为了构造齐次式，以实现基本不等式“二定”这个条件.

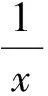
当且仅当a=b时取到等号.具体解法如下(思路6)：

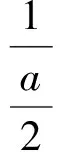
从而

于是

当且仅当a=2b，即a=4,b=2时，取到等号.

从而

当且仅当m=n，即a=4,b=2时，取到等号.

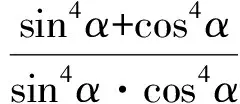
由ab-a-2b=0，得

当且仅当a=4,b=2时，取到等号.

生10：生9的解法也可以这样处理(思路10)：

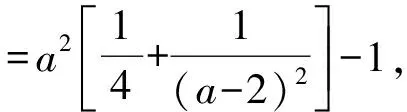
当且仅当a=4,b=2时，取到等号.

生11：我用消元法消去字母a(思路11)：

由ab-a-2b=0，得

令b-1=m，则b=m+1,从而

当且仅当m=1，即a=4,b=2时，取到等号.

师：生9、生10、生11都由教材得到本题的第4个“根”，然后用消元法将双变量问题转化为单变量问题，再利用基本不等式和权方和不等式求得最小值.还有其他想法吗？

生12：我想起第二次模拟考试第14题用到的“切线放缩法”(思路12)：

a+2b≥8，

所以

2a+4b-9≥2×8-9=7,

当且仅当a=4,b=2时，取到等号.

生13：我用的是“切线放缩法”加“1的代换”(思路13)：

2a+4b-9=

当且仅当a=4,b=2时，取到等号.

师：生12和生13联想到第二次模拟考试第14题，利用“切线放缩法”将二次式放缩为一次式，进而利用“基本不等式”或“1的代换”求得最小值.

生14：本题的目标是求最小值，而我们常利用导数研究函数的最值(思路14)：

先消元：由ab-a-2b=0，得

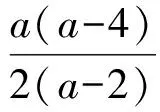
令f′(a)=0,得a=0(舍去)或a=4.当a∈(2,4)时，f′(a)<0，f(a)单调递减；当a∈(4,+∞)时，f′(a)>0，f(a)单调递增,从而

f(a)min=f(4)=7，

此时a=4,b=2.

师：生14是从本题的目标入手，寻找到了本题的第5个“根”：求最值.想到消元，构造新函数，用导数这个工具来求函数的最小值，非常巧妙.通过上面的分析，你能学到些什么呢？

生15：当我们遇到一个难以下手的题目时，首先要分析题目的条件，看看条件可以如何转化；其次再分析题目的所求，看看有什么相应的方法；再分析本题所考查知识点所属的模块，联想本知识点常用的解题思路和方法.

师：一位苏联数学家说过：解题——意味着将要解的问题转化为已经解过的问题.生15总结得非常好，当拿到一个较难的题目时，我们可以从3个角度进行思考：条件、目标、所属知识模块，最终都将回到我们曾经解答过的问题，尤其是熟悉的教材、练习册以及考试做过的题目等等.“条条大路通罗马”，只要我们不气不馁，回归教材，总能寻找到题目的“根”，从而找到解决问题的方法.

师：最后给同学们准备了几道题供课后去思考.相信同学们通过今天的探究活动，会有更多的收获.

课后思考题：

4.已知a,b,m,n均为正数，且a+b=1，mn=2,求(am+bn)(bm+an)的最小值.

3 课后反思

3.1 回归教材寻题根

回归教材怎么回？教材是考试内容的具体化，是高考试题的主要来源之一，由针对性原则可知，回归教材是提升复习效率的有效手段[2].很多学校都是在高考前留两周的时间，教师跟学生一起翻教材、看例题和习题.这样的回归教材是低效的，笔者认为回归教材应该贯穿在整个高三复习的始终.在复习的过程中，一旦遇到与教材典型例习题有关，而学生又掌握不佳的问题时，就应该翻出教材，及时发现教材例习题中所蕴涵的丰富的数学思想和数学方法.要探究试题与教材例习题的结合点，善于在教材中寻找试题的原型，通过分解、整合、拓展，引导学生在变化中发现不变的规律，避免学生机械重复.一些看似平淡无奇的习题，也许有着意想不到的功能，教材中的习题若仅停留在它的表面，而不探究它的本质，则会失去习题的内涵与新意，也会失去提升学生学习能力的良机，不利于教学的开展与深入.

题根是什么？题根就是那些源于基础又高于基础，提炼于解题实践又能广泛用于解题实践的结论、习题、例题、各类试题[3].通过对题根的挖掘和思考，可以清楚地掌握基本知识和方法，领悟数学问题的本质，从而有助于脱离“茫茫题海”，“一题可破万题山”.在平时的解题训练中，若能重视题根及其应用，则能举一反三，跳出题海，并提高解题能力.著名数学家苏步青曾说:“学习数学要多做习题，边做边思索.先知其然，然后知其所以然.”教师要在平时的教学中重视教材，教材中有大量值得教师与学生一起探究与学习的材料(包括题根)，教师应充分利用这些资源，引领学生进行探究，做到触类旁通、心中有数，激发学生的学习兴趣，使学生在探究中提高基本技能.

3.2 深度学习悟本质

深度学习是学生源于自身内部动机,对有价值的学习内容展开的完整的、准确的、丰富的、深刻的学习.它是一种有意义的学习，要求学生的学习不是单纯的接受，而是在发现基础上的同化；它也是一种理解性的学习，重在引导学生通过深切的体验和深入的思考，达成对学科本质和知识意义的理解渗透[4].深度学习提倡将新知识与已知概念和原理联系起来，整合到原有的认知结构中，从而引起对新的知识信息的理解、长期保持及迁移应用[5].深度学习是内源性的学习，让学生积极主动地参与到课堂教学活动中，学生的学习才有可能是有深度的，也只有学生深度学习，才可能促进学生发展核心素养.准确把握学情和深刻解读教材就显得尤为重要，因为它们是引导深度学习的基点.

德国教育家第斯多惠指出：“不好的老师转述真理，好的老师教学生去发现真理.”有效的教学活动应该引导学生通过动手实践、自主探索，达到叶圣陶所说的“教是为了不教”的境界，最终的目的是使学生感悟数学的精髓，培养学生分析问题和解决问题的能力.

[1] 谢永广.试卷讲评课的教学思考[J].中学数学，2017(4)：20-22.

[2] 刘国祥.探究·溯源·拓展·启迪[J].中国数学教育，2017(3)：51-53；56.

[3] 蓝云波.两道试题，同一题根[J].数学通讯，2015(12)：30-32.

[4] 贺慧.回归课堂原点的深度学习论[J].基础教育课程，2015(12)：8-13.

[5] 安富海.促进深度学习的课堂教学策略研究[J].课程·教材·教法，2014(11)：57-62.

2017-09-10

任卫兵(1983-)，男，江苏连云港人，中学一级教师.研究方向：数学教育.

O122． 1

A

1003 - 6407(2017)11-19-05