误差思想在数学高考中的应用*
●关丽娜 ●钟德光 ●郑伟庭
( 深圳大学数学与统计学院,广东深圳518060) ( 广州大学数学与信息科学学院,广东广州510006) ( 平山第三中学,广东惠东516300)
误差思想在数学高考中的应用*
●关丽娜 ●钟德光 ●郑伟庭
( 深圳大学数学与统计学院,广东深圳518060) ( 广州大学数学与信息科学学院,广东广州510006) ( 平山第三中学,广东惠东516300)
文章从简单的二阶矩阵不满足乘法交换律的例子入手,说明构造“误差”矩阵的原因,再由这种误差思想引入偏右( 偏左) 对称函数、偏右( 偏左) 等比数列等定义. 接着,探索了这些定义的一些简单性质,并利用这些性质解决了一些数学高考压轴题.
误差思想; 严格偏右( 偏左) 对称函数; 正项偏右( 偏左) 等比数列
先从一个关于矩阵的简单例子讲起.关于矩阵的简单的初步认识可参见高中《数学(选修4-2)》.考察二阶矩阵
我们说两个矩阵A,B相等指的是
a11=b11,a12=b12,a21=b21,a22=b22.
对于矩阵A,B,经典的减法运算定义如下:
经典的乘法运算定义如下:
对实数乘法运算,我们都知道它是满足交换律的.但是对于矩阵的乘法运算,它一般是不满足交换律的,即并非所有矩阵都满足A·B=B·A,如:
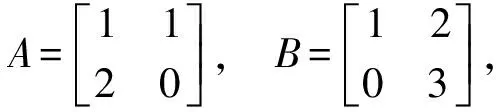
则
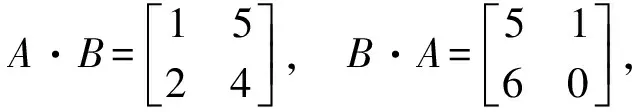
显然,A·B≠B·A.既然并非所有矩阵都满足交换律,那么可以构造一个如下的矩阵C,
C=A·B-B·A.
为什么要引入矩阵C呢?因为并不是所有矩阵A,B都满足交换律,所以考虑它们偏离满足交换律的程度,也就是引入了一个“误差”矩阵C.显然当C为零矩阵时,A,B就满足乘法交换律了.千万别小看这种误差思想,流行理论中著名的普阿松括号积[1]就是这样构造的.普阿松括号积在流形上的微积分中具有重要的作用,许多重要概念与它有直接联系,比如局部1参数群.因此构造普阿松括号积的思想(即误差思想)也深受高考命题者的关注.另外,因为不等式是高中数学的重要内容之一,而误差思想又涉及不等式,所以它自然而然深受命题者的青睐.
其实误差思想在高中数学中有很多应用,如以下命题:
命题1设函数f在实数R上有定义,且设A为一个给定的实数.设f在(-∞,A)上单调递减,在[A,+∞)上单调递增,且对于所有的x∈R,有f(x)=f(2A-x).若x1,x2为方程f(x)=c(其中f(A)>c)的两个零点,则x1+x2=2A.
显然并不是所有定义在实数R上的函数f都是对称函数,这很容易举出例子来.但是受误差思想的启发,我们可以构造一个关于函数f的误差函数Ff:
Ff(x)=f(x)-f(2A-x).
显然,当对所有的x∈R,若Ff(x)=0,则f就是对称函数了.可见函数Ff是对称函数f的推广.虽然并非所有定义在实数R上的函数f都是对称函数,但是庆幸的是,当Ff与f满足一定条件时,f具有类似于命题1的性质:
命题2设函数f在实数R上有定义,且设A是一个给定的实数.设f在(-∞,A)上单调递减,在[A,+∞)上单调递增,且对于所有x∈R,Ff在(A,+∞)上为正函数.若x1,x2为方程f(x)=c(其中c>f(A))的两个零点,则x1+x2<2A.
证明不妨设x1
f(x2)-f(2A-x2)>0.
又因为f(x2)=f(x1)=c,所以
f(x1)-f(2A-x2)>0,
即
f(x1)>f(2A-x2).
由于f在(-∞,A)上单调递减,且x1 在上述讨论中,若当x∈(A,+∞)时,Ff(x)≥0恒成立,则称函数f为偏右对称函数;同样地,我们也可以引入偏左对称函数,只要求Ff在(-∞,A)内恒为非负即可.若当x∈(A,+∞)时,Ff(x)>0恒成立,则称函数f为严格偏右对称函数;若当x∈(-∞,A)时,Ff(x)>0恒成立,则称函数f为严格偏左对称函数.关于高考对严格偏右对称函数的考查,如2016年全国数学高考卷Ⅰ的函数压轴题. 例1已知函数f(x)=(x-2)ex+a(x-1)2有两个零点. 1)求a的取值范围; 2)设x1,x2是函数f的两个零点,证明:x1+x2<2. 分析1)a的取值范围为(0,+∞),解答过程略. 2)从求证的结果来看,结合命题2,可知f应该是严格偏右对称函数,且A=1.容易证明当a>0时,f在(-∞,1)上单调递减,在[1,+∞)上单调递增.因此,只需要考虑f的误差函数Ff(x)=f(x)-f(2-x)在(1,+∞)上恒大于0即可.因为Ff(x)=(x-2)ex+xe2-x,所以 又因为函数ex-e2-x在(1,+∞)上单调递增,所以 ex-e2-x>0. 因此,当x∈(1,+∞)时,Ff(x)>0,即Ff在(1,+∞)上单调递增,故 Ff(x)>Ff(1)=0. 显然若对于所有的n∈N*,Fan(n)≡0,则{an}是公比为q的等比数列.由此可见,Fan(n)是等比数列{an}的推广.类比于偏右(偏左)对称函数,可以引入偏右(偏左)等比数列的定义:若对于所有的n∈N*,Fan(n)≥0(≤0),则称数列{an}为偏右(偏左)等比数列;若对于所有的n∈N*,Fan(n)>0(<0),则称数列{an}为严格偏右(偏左)等比数列.等比数列的通项公式可以表示出来,对于偏右等比数列,我们亦有以下类似结论: 命题3设正项数列{an}满足:对于所有的n∈N*,Fan(n)≥0,且q>0,q≠1,则 an≥a1·qn-1. 证明过程比较简单,此处略去. 1)证明:|an|≥2n-1(|a1|-2); (2016年浙江省数学高考理科试题第20题) 此题的本质是偏右等比数列.在此我们只讨论第1)小题. 证明若|a1|≤2,则结论显然成立,因此不妨设|a1|>2.以下证明对于所有的n∈N*,|an|>2.这是因为由绝对值不等式可得 即 |an+1|≥2|an|-2. 于是由数学归纳法容易得出对于所有的n∈N*,|an|>2. 另外,因为|an+1|≥2|an|-2,所以 |an+1|-2≥2(|an|-2). 由于对于所有的n∈N*,|an|-2>0,从而数列{|an|-2}为正项偏右等比数列,且q=2.由命题3可得 |an|-2≥2n-1(|a1|-2), 故 |an|≥2n-1(|a1|-2). 例3已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(其中n∈N*).证明:当n∈N*时, 1) 0 (2017年浙江省数学高考试题第22题) 我们只讨论第3)小题. 证明对于所有的x>-1,ln(1+x)≤x.由第1)小题可知,对于所有的n∈N*,有xn>0,从而 xn=xn+1+ln(1+xn+1)≤xn+1+xn+1=2xn+1. 另外,由第2)小题可得 由第1)小题可得对于所有的n∈N*,xn 即 亦即 由上面的讨论可以看出,误差思想在高中数学的应用主要是对一些涉及到等号的数学定义引入相应的误差即可.比如等差数列可以引入偏右(偏左)等差数列;奇函数可以引入偏右(偏左)奇函数;周期函数可以引入偏右(偏左)周期函数等等.这就可以产生很多的不等式,从而为命题者提供丰富的命题材料. 误差思想不但在现代基础数学中有重要的应用,而且能够提供丰富的不等式.此外,引入函数f的误差函数Ff也是函数f的某种性质的推广.从2016年和2017年的浙江省数学高考理科数列压轴题来看,它们都考查了误差思想.这一方面说明了命题者对误差思想的重视;另一方面,以误差思想命题,不但能与现代数学知识联系起来,而且又不超出高中数学的考试大纲,这不得不感叹命题者的水平之高啊! [1] 陈维桓.流行上的微积分[M].北京:高等教育出版社,2003. 2017-07-13 关丽娜(1992-),女,广东阳江人,硕士研究生.研究方向:数学教育. O1 A 1003 - 6407(2017)11-32-03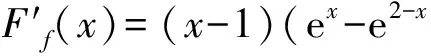
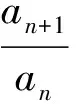
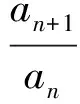
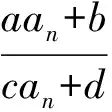
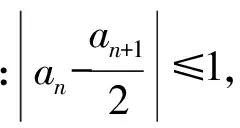
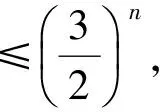
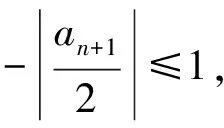

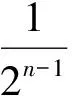
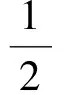
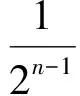
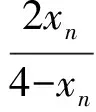
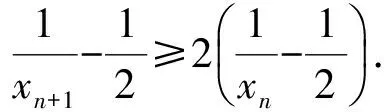

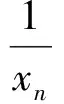
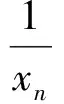
——特级教师周卫东《乘法交换律》教学赏析
——特级教师周卫东苏教版四下《乘法交换律》教学赏析

