揭示数学本质 培养思维能力*——以“高考中多元变量的最值和范围问题”为例

●

(建湖高级中学,江苏 建湖 224700)

揭示数学本质培养思维能力*
——以“高考中多元变量的最值和范围问题”为例

●张立建潘培彬沈立国

(建湖高级中学,江苏 建湖 224700)

高中数学教学的目的是帮助学生形成理性逻辑思维、发展学生的思维能力和创新意识． 数学教学要“授人以渔”，揭示数学问题的实质，帮助学生掌握解决问题的方式、方法，从而提高学生自身的知识水平和认知能力，形成自己的数学能力和素养．

三角形中的最值与范围问题; 多元最值; 学生数学思维的培养

高考注重对基础知识、基本技能、基本数学思想方法以及基本经验积累的考查，加强了对理性思维的考查，突出对数学的理解以及创新应用能力的考查．既注重知识与能力，又体现数学素养；既注重思想方法，又突出创新意识；既注重选拔功能，又兼顾中学教学．高三复习要在学生有一定的基础和思维知识体系后设计专题复习，从而培养学生的综合能力和数学素养，这也是数学教学的目的.

1 基本情况

1.1 学情分析

学生是江苏省四星级高中高三学生，思维较好.学生经过一轮复习和综合训练，知识体系已经形成，解题经验丰富，如在三角变换、正余弦定理、函数思想、线性规划、几何意义等方面都有了“量”的积累.但信息量大、字母多、式子烦、难度大、综合性强的题目，学生“分析问题、发现联系、确立目标、解决问题”的能力还没有形成.

1.2 教材分析

三角形中的最值和范围问题及多元变量的最值问题是高考的热点之一，多为压轴题.此类问题兼具知识的综合性、思想方法的一般性、形式的灵活性，能较好地考查基础知识、基本方法和基本能力，及学生对知识的综合应用能力和迁移能力，具有很强的选拔功能.因此，笔者选择本课题进行学习和探究，以提高学生解决问题的能力.

1.3 教学目标

1)掌握三角形中二元、三元最值和范围问题的解法；2)建立多元目标意识，掌握多元最值问题的求解策略；3)体会数学解题中的整理，由整理实现内化,由拓展实现知识的整合与串联，提高综合应用能力.

教学重点多(三)元变量最值或范围问题.

教学难点形成数学综合应用能力，提高对数学实质的认识.

2 教学过程

2.1 引例

提出本节课要解决的问题，即高考中的多元问题.

例1在锐角△ABC中，若sinA=2sinBsinC，则tanAtanBtanC的最小值是______.

(2016年江苏省数学高考试题第14题)

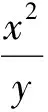
(2010年江苏省数学高考试题第12题)

(2012年江苏省数学高考试题第14题)

(2014年辽宁省数学高考试题第16题)

2.2 练一练

“基础训练，追本溯源”是巩固三角形中二元最值和范围问题的基本策略，明确该类问题在方法、数学思想等方面的实质，为解决多元变量问题作好铺垫.

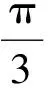
(2014年江苏省数学高考试题第14题)

(2008年江苏省数学高考试题第13题)

2.3 悟一悟

三角形中的最值和范围主要是关于边、角、面积的范围和最值问题.例5由外接圆直径易想到正弦定理，从而转化为三角函数问题；例6由齐次式易得边的关系，由目标函数想到余弦定理，实现条件和目标的串联，顺理成章，消元后根据平方和结构，自然想到基本不等式放缩；例7学生很容易想到下面的解法1，即建立边的一元函数，求最值，但运算量大.解法2(即利用圆的第二定义)不容易想到，需要一定的知识和能力储备.

通过基础训练，学生自行归纳得出解决三角形中最值或范围问题的方法主要有两类：1)代数法，函数思想、二元基本不等式放缩等；2)几何法，平面几何(三角形任意两边之和大于第三边)、解析几何(几何意义、线性规划).下面对例7进行详解：

解得

由余弦定理,得

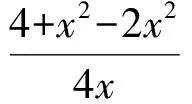
于是

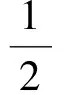
解法2(解析法)以线段AB所在直线为x轴、线段AB的中垂线为y轴建立平面直角坐标系，则A(-1,0),B(1,0).设点C(x,y)，则

化简得

(x-3)2+y2=8(其中x≠0)，

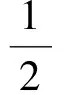
2.4 自主探究，让学引思

设计意图将三角形中的二元问题上升为三元问题，突出减元化为二元问题的指导思想.

例8在锐角△ABC中，若sinA=2sinBsinC，则tanAtanBtanC的最小值是______.

(2016年江苏省数学高考试题第14题)

设计意图由练一练中的三角形二元问题过渡到三角形中三元变量问题，比较自然.关键是解题思路的启发，引导学生建立消元的意识，消元转化为二元最值问题，再用代数方法、函数思想或基本不等式求最值.

分析本题是三元变量问题，消元并运用转化思想化为一元、二元为主要策略.

问题1先说条件，由sinA=2sinBsinC，能想到什么？(直觉思维.)

生：第一直觉应该是应用正弦定理，但结构不对称，同时目标函数tanAtanBtanC无法用边表示.

追问：还有怎样的认识？(分析、联想.)

生：有3个角，需消元，想到内角和定理，利用sinA=sin(B+C)化简sinA=2sinBsinC可得

sinBcosC+cosBsinC=2sinBsinC，

再结合目标，弦化切，齐次结构同除以cosBcosC可得

tanB+tanC=2tanBtanC.

问题2再看目标，由tanAtanBtanC的最小值想到什么？

生：消元转化为二元目标函数，再求二元最值，预示着两个解题方向:1)函数最值;2)基本不等式.

(学生做题，教师投影学生的答题情况.)

问题3本题与练一练中例5和例6有何联系？

解法1因为sinA=2sinBsinC，sinA=sin(B+C)，所以

sinBcosC+cosBsinC=2sinBsinC,

两边同除以cosBcosC,得

tanB+tanC=2tanBtanC.

(此时问题转化为二元变量最值问题.求解二元最值问题是学生比较熟悉的，因此他们的思维比较活跃，角度不同、理解不同，解法精彩.观察到和式tanB+tanC与积式tanBtanC及关系tanB+tanC=2tanBtanC，可消去和式，将积式看作自变量.)

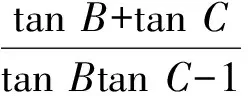
当且仅当t=2时，等号成立.故所求的最小值为8.

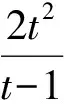
解法2(切化弦)由sinA=2sinBsinC，知

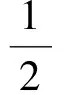
因为 cosA= -cos(B+C)=

-cosBcosC+sinBsinC，

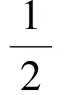
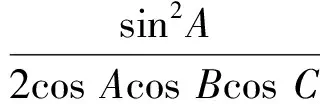
当且仅当tanA=4时，等号成立.

师：以上方法都是消元的方法，还有其他不同的见解吗？

生：解法3由解法1得

tanB+tanC=2tanBtanC，

从而目标函数

tanAtanBtanC=tanA+tanB+tanC=

tanAtanBtanC≥8.

问题4你有什么收获？

生：先追本溯源，看清是哪类问题.分析结论建立目标意识，结合条件，联想发散，找到之间的联系，获得解题途径.

师：非常好！我们要学会解决问题的方法，学会发现数学问题的实质.

点评本题的核心是如何消元，常见的消元方法有：整体换元、齐次结构化为整体、代入消元.

下面小组合作，解决例9.

例9在△ABC中，角A,B,C所对的边分别为a,b,c，若a2+b2+2c2=8，则△ABC面积的最大值为______．

(江苏省盐城市2017届高三一模试题第14题)

分析以下解法1由平方和入手，想到余弦定理；解法4由平方和想到圆的方程.

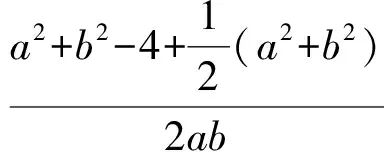
当且仅当a=b时，等号成立.于是

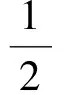
平方得

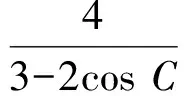
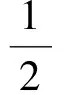
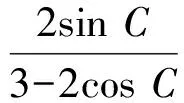
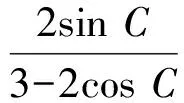
解法3由三角形面积公式可得

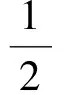
即

亦即

因为a2+b2+2c2=8，所以

a2+b2=8-2c2，

解法4取线段AB的中点为原点、线段AB的中垂线为y轴建立平面直角坐标系.设A(-m,0),B(m,0),C(x,y),则

8m2+(x-m)2+y2+(x+m)2+y2=8，

化简得

x2+y2+5m2=4.

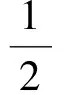
于是由基本不等式得

故

点评学生容易想到的方法，主要是解法1和解法3，其实质是化为边的函数；解法2主要利用角，化为三角函数，这也是三角形问题的基本处理方式.

2.5 拓展延伸

由特殊到一般，将三角形中多元变量的解题思想和解题方法，应用到一般情形，从而真正帮助学生实现思维的跨越，达成自己分析条件、建立目标、转化化归(消元)、求解(解模)的能力.

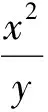
(2010年江苏省数学高考试题第12题)

分析本题实际上是二元不等关系下二元函数的最值问题.若注意到已知条件的同正同向性，则可换元，利用不等式的性质(正项不等式的同向可乘性)求解.若注意到已知条件的次数，则可取对数将已知条件转化为线性关系，用线性规划求解.

从而

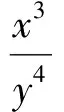
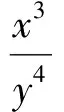
解法2由题意得x,y是正数，已知条件取对数得

令a=lgx，b=lgy,则问题转化为已知实数a,b满足

求3a-4b的最大值.下面用线性约束条件下的线性目标函数的几何意义求解(略).

2.6 小结

1)指导思想：多元化二元；2)消元的方法：常用的消元法有代入消元、整体换元、三角换元、选主元等，特别注意齐次分式和齐次多项式，还有和式、积式、平方和的结构关系以及公式的几何意义；3)选择求值或范围的方法主要有：建立函数、利用基本不等式放缩、利用方程的判别式、利用动点的轨迹、利用斜率与距离的几何意义、利用类线性规划.

3 回顾与反思

3.1 教学设计的基本立意

本节课的目标：一是引导学生将所学知识“连珠编网”，学会分析与整合，完成“知识的迁移”；二是掌握探究问题的方式和提高知识迁移、综合应用的能力.

本节课的一条明线：三角形中的二元最值和范围问题—三角形中的三元问题—一般情形中的多元最值和范围问题.一条暗线：解法上，从代数方法(函数、方程、不等式、解析几何)到几何方法(数形结合、线性规划、几何意义).

解题途径：一方面，树立目标意识，寻找问题本源，看透数学实质，回忆解题通法；另一方面，要注重问题的分析、条件的转化，作好知识的串联.

3.2 教学反思

1)立足学生的认知基础，从学生熟悉的三角形中二元最值问题的解决策略引出本节课.学生较熟悉，题目易求解，起点低，学生易融入课堂.

2)突出学生的主体地位，激发学生的探索精神.

在一节课中，学生的发展来自于自己的积极思考与主动探究，取决于自己对知识的认识深度、广度和探究过程中问题的参与度.本节课的安排循序渐进，由易到难，由简及繁，由浅入深，呈螺旋式上升，有利于激发学生的探究兴趣，激发学生的发散思维，最大限度地拓展学生思维的广度和深度.

3)重视知识生成，培养学生思维的创造性.

本节课学生入手容易，解决方法多，采用“头脑风暴法”，激发创新思维;从基础出发产生联想反应，形成思维碰撞;在平等的气氛中，集体讨论，相互感染激发兴趣，让每个学生都得到不同程度的提高.

4)本节课“生长点”的再利用.本节课容量大，因此后续知识可以由学生自主探究完成.

5)运用多种数学思想方法：转化化归、数形结合、函数与方程.

本节课培养了学生的数学兴趣和探究精神，提高了学生分析、综合、应用等能力.

2017-08-21

张立建(1982-)，男，山东青州人，中学一级教师.研究方向：数学教育.

O12

A

1003 - 6407(2017)11-01-05