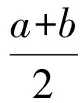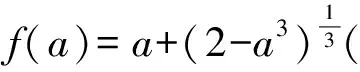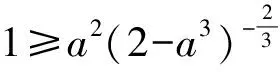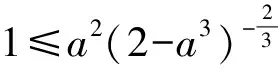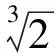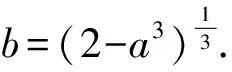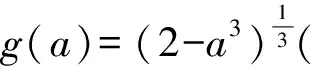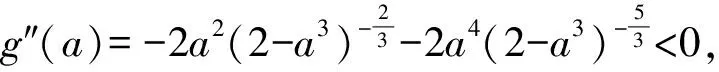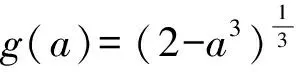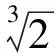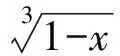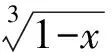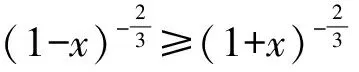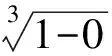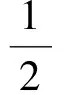2017年全国数学高考卷Ⅱ第23题的11种证法及其感悟*

●

(北仑明港中学，浙江 宁波 315806)

2017年全国数学高考卷Ⅱ第23题的11种证法及其感悟*

●甘大旺

(北仑明港中学，浙江 宁波 315806)

文章指出2017 年全国数学高考卷Ⅱ第23 题第2) 小题的测试区分度较强，探究此题不同于参考答案的其他 11 种证法，其中简述两个数学史结论，最后因势利导地得出3 个概括、深化、类比的定理．

排序不等式; 切比雪夫不等式; 琴生不等式; 拉格朗日乘数法

2017年全国数学高考卷Ⅱ由21道必考题和两道选考题构成，其中理科卷和文科卷的最后一道选考题(即全卷最后一题)是相同的，即：

题目已知a>0，b>0，a3+b3=2，证明：

1) (a+b)(a5+b5)≥4；

2)a+b≤2.

第1)小题比较简单，第2)小题对考生的测试区分度明显强于第1)小题.命题组提供第2)小题的证明思路是展开(a+b)3后运用均值不等式，这属于通法[1].下面探索第2)小题的其他11种证法.

证法1要证明a+b≤2，只要证

23≥(a+b)3=a3+b3+3(a2b+ab2),

即

8≥2+3(a2b+ab2)，

亦即

a2b+ab2≤2=a3+b3，

即

(a-b)2(a+b)≥0.

由a>0且b>0,知上式显然成立，故

a+b≤2.

证法2将方法1(分析法)改写成反证法.

假设a+b>2，则

23<(a+b)3=a3+b3+3(a2b+ab2)，

即

8<2+3(a2b+ab2)，

亦即

8<2+3(a2b+ab2)，

从而

a2b+ab2>2=a3+b3，

移项分解，得

-(a-b)2(a+b)<0，

于是

a+b<0，

这与已知条件a>0，b>0矛盾.因此假设不成立，故a+b≤2.

证法3假设a+b>2，即b>2-a，则

b3>(2-a)3=8-12a+6a2-a3.

又a3+b3=2，从而

2>8-12a+6a2=2+6(1-a)2，

于是

0>(1-a)2，

这是自相矛盾的.因此，假设不成立，故a+b≤2.

证法4由a>0,b>0,得

0<4ab≤(a+b)2，

从而 2=a3+b3=(a+b)(a2-ab+b2)=

(a+b)[(a+b)2-3ab]≥

于是

(a+b)3≤8，

故

a+b≤2.

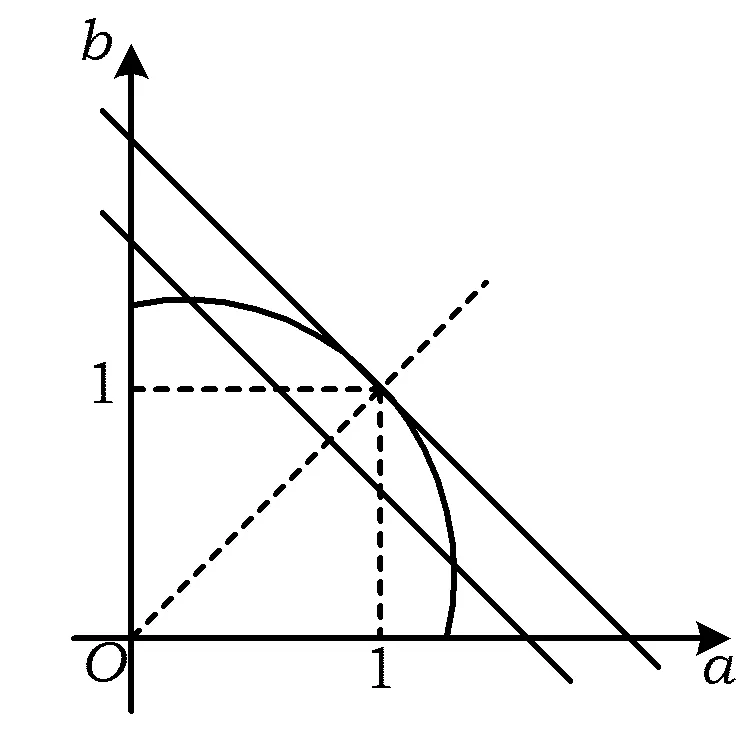
证法5不妨取0

ab2+ba2≤a·a2+b·b2=a3+b3.

又2ab≤a2+b2(均值不等式)，从而

(a+b)3= (a2+2ab+b2)(a+b)≤

2(a2+b2)(a+b)=

2(a3+b3+ab2+a2b)≤

2(a3+b3+a3+b3)=

4(a3+b3)=8,

故

a+b≤2.

预备知识1[2]俄国数学家切比雪夫在代数学上提出一个不等式：

(其中a1≤a2≤a3≤…≤an,b1≤b2≤b3…≤bn，n-1∈N+，两处“≤”取到等号的充要条件是a1=a2=a3=…=an且b1=b2=b3…=bn).

证法6不妨取0

(a+b)3= (a+b)(a+b)(a+b)≤

2(a2+b2)(a+b)=4(a3+b3)=8,

故

a+b≤2.

证法7取函数f(x)=x3(其中x>0)，则一阶导数f′(x)=3x2，二阶导数f″(x)=6x>0，从而f(x)在(0,+∞)内上凹.运用琴生不等式得

从而

故

a+b≤2.

证法8由a3+b3=2(其中a>0且b>0)解得

从而

则

故

a+b≤2.

则

图1

在图1所示的直角坐标系aOb中，函数b=g(a)的图像，即曲线段a3+b3=2(其中a>0且b>0)关于直线b=a对称，于是该曲线段与平行直线系a+b=m(其中m为截距参数)有公共点的充要条件是

故

a+b≤2.

证法10根据已知条件作均值代换a3=1-x,b3=1+x(不妨设a≤b而取0≤x<1)，则

因此，函数h(x)在定义域[0,1)上单调递减，即

故

a+b≤2.

预备知识2[3]为了探求二元函数f(x,y)在约束条件φ(x,y)=0下的极值点，出生于意大利的法国数学家拉格朗日借用偏导数发现了“乘数法”——如果二元函数f(x,y)在约束条件φ(x,y)=0下连续并存在偏导数，取函数L(x,y)=f(x,y)+λφ(x,y)，那么目标函数f(x,y)的所有极值点(x0,y0)适合于方程组

证法11依题意，不妨取拉格朗日函数L(a,b)=a+b+λ(a3+b3-2)，其中a>0且b>0，则列方程组

消去乘数λ,解得a=b=1.

此时，二元函数u(a,b)=a+b的唯一极值是

a+b=1+1=2.

于是，运用拉格朗日乘数法知，2是a+b的最大值，故a+b≤2.

回眸上述题意及证题思路，得到以下3个定理：

定理1如果两个正数a与b满足an+bn=c，其中两个常数c>0,n∈N+且n≥2，那么

当a=b时，上述不等式取到等号.

进一步推广定理1的结论，可以验证得到：

定理2如果两个正数a与b满足am+bm=c，其中两个常数c>0,m>1，那么

当a=b时，上述不等式取到等号.

对定理2进行类比思考，可以得到：

定理3如果两个正数a与b满足am+bm=c，其中两个常数c>0,m∈(0,1)，那么

当a=b时，上述不等式取到等号.

[1] 甘大旺.通法与特技的相对性及启示[J].数学通报，1997(2)：11-12.

[2] 甘大旺.切比雪夫不等式及其两个推论[J].数学通讯,2016(12)：59-61.

[3] 甘大旺.拉格朗日乘数法的初等应用[J].宁波教育学院学报，2017,19(1)：134-137.

2017-09-08

甘大旺(1959-)，男，湖北咸宁人，湖北省特级教师.研究方向：数学教育.

O122． 3

A

1003 - 6407(2017)11-17-03