对三角形“四心”向量表示的思考*

●

(萧山中学,浙江 杭州 311200)

对三角形“四心”向量表示的思考*

●金灿芳

(萧山中学,浙江 杭州 311200)

三角形中重心、内心、外心、垂心的向量表示是高考复习的热点内容之一，值得我们关注． 文章通过向量加法的平行四边形法则以及正弦定理，总结了解决此类问题的通法，并揭示了解决数学问题要淡化技巧，注重本质．

向量; 正弦定理; 心; 本质

在日常生活中，一条大路的尽头会有很多分岔，有各自的风景.而数学中，几个看似独立的题目，其本质可能是一样的，可以从同一个角度去解释.

1 问题展现，解决问题

( )

A.外心 B.内心 C.重心 D.垂心

高一学生拿到该题，大多毫无头绪，困难很大.学生乐于见到另一种形式的题，见变式1和变式2.

下面我们来解决例1：先排除重心和内心，将已知式变形为

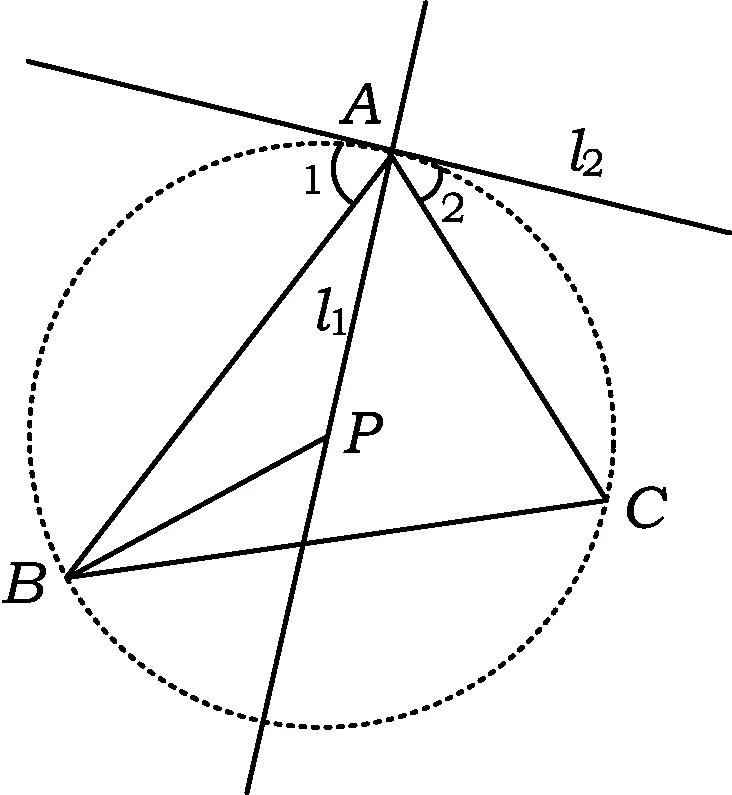
图1

2 探究问题,挖掘联系

已经有了3个“心”的表达方式，那么垂心是否有类似的表达呢？

例2的答案正是垂心.下面探讨的是两个例题和两个变式之间的联系，是否有统一解法？

如图2，过点A作直线与AP所在的直线垂直，在AB,AC上分别取点E,F，使得

图2 图3

两个变式也可以从以下角度解释:在变式2中，

在变式1中，

图4

于是 |AB|sinα=|AC|sinβ，

进一步可得

|AB|·|AP|sinα=|AC|·|AP|sinβ,

即

S△ABP=S△ACP,

因此点P在BC的中线上，AP过△ABC的重心.

上述通法对变式1来说有点繁琐.下面看例2：

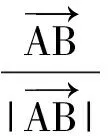
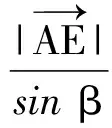
即

以上均是以AP为对角线构造平行四边形，通过正弦定理得到关于α,β的等式，从而确定AP过什么心，至此三角形的4个“心”的向量表达式得到了完美的统一.

图5

3 运用通法，巧妙解题

解由题意得

如图5，作出相应的平行四边形，在△AEO和△ABC中利用正弦定理，得

因为点O为△ABC外接圆的圆心(设⊙O的半径R),所以

故

m=sinθ.

本题利用三角形的外心，构造相应的平行四边形性质，通过正弦定理联系各个变量，顺利解决问题.

4 深入本质，诠释巧合

我们再来看两道浙江省数学高考试题：

例4已知平面向量α,β(其中α≠0,α≠β)满足|β|=1，且α与β-α的夹角为120°，则|α|的取值范围是______.

这两道题咋一看没什么联系，其实题干条件都是向量的线性运算，结论都是求边的范围，因此这两道题考查的本质是一样的：向量线性运算的几何意义和正弦定理的应用.

大多数教师在复习时都会强调“抓住本质”，那么在实际的操作中，我们应该怎么做呢？其实本质就蕴含在概念、性质、结论等的发生处.数学概念是进行数学推理、判断、论证的重要依据，概念学习的核心任务就是要体会概念产生、发展的过程，理解概念的本质[2].有些数学概念或结论可能需要物理背景帮助理解，比如向量和向量的数量积；有些需要直观的动画学生才能体会，比如三角函数图像的变换，先平移和先伸缩对于平移量的影响；有些需要学生自己动手印象才深刻，比如椭圆、双曲线的定义等.教师和学生不妨放慢脚步，让教学进度、题海战术先靠边，师生一起探索，动手实践，交流合作，从而启发学生发现生活中的数学，欣赏数学的严谨，惊叹数学的美.

[1] 中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2004：3-5.

[2] 易文辉.体验概念生成 促进思维发展——以“充分条件与必要条件”(新授课)为例[J].中学教研(数学)，2016(9):15-18.

2017-09-20

金灿芳(1982-),女,浙江萧山人,中学一级教师.研究方向:数学教育.

O123． 1

A

1003 - 6407(2017)11-30-03