探究一道导数试题的命题手法及应用*
● ●
(泉州市第五中学,福建 泉州 362000) (泉州市实验中学,福建 泉州 362000)
探究一道导数试题的命题手法及应用*
●杨苍洲●崔红光
(泉州市第五中学,福建 泉州 362000) (泉州市实验中学,福建 泉州 362000)
文章通过探究一道导数压轴试题的命题手法,得到一种“以直代曲”的命题方法,并应用此方法命制出两道具有一定难度的导数试题.
命题手法; 以直代曲; 试题命制
在学校的一次单元测试中,命题教师选用了一个网题作为试卷的压轴题.大部分学生和教师都感觉本题难以下手,过后在研究网络提供的试题答案时,也因为答案的神来之笔而感觉到一头雾水.为了彻底研究清楚此类试题的解题方法,笔者对试题的命题手法进行探究.只要探明命题者的命题思路,顺着命题思路进行解题,解题就显得自然、流畅[1].
1 题目展示
例1已知函数f(x)=(x+1)lnx-a(x-1).
1)若函数f(x)的图像与直线y=x-1相切,求实数a的值;
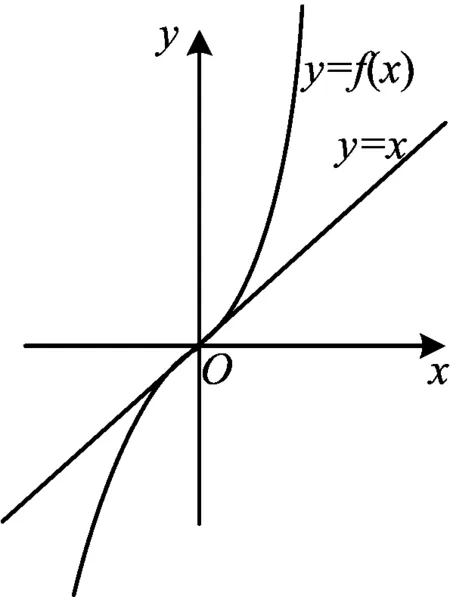
2)当1 笔者首先思考,命题者如何构造出第2)小题中的不等式?接着思考,第1)小题对第2)小题是否有承上启下的作用?带着这个疑问,结合平时的解题、命题经验,笔者开始了试题命题手法的探究之旅. f(x)=(x+1)lnx+(c-1)x+d, 其中c,d可以根据需要进行调整. 第二步:设定函数在拐点处的切线.命题者设定函数在拐点(1,0)处的切线为y=x-1,则由f′(1)=1,f(1)=0,可知c=0,d=1,此时, f(x)=(x+1)lnx-(x-1). 由此,命题者找到了试题的背景函数. 第三步:进行合理设问.一道试题的几个设问往往具有一定的相关性,设问与设问之间呈现层层递进的关系.第1)小题常常是第2)小题的台阶,为第2)小题的解答提供方向,埋下伏笔. 命题者在题干中引入参数a,使函数变为 f(x)=(x+1)lnx-a(x-1), 并在第1)小题中提供条件“函数f(x)的图像与直线y=x-1相切”,从而求出实数a的值. 图1 第1)小题的设置,除了考查导数的几何意义外,也引导解题者去探究“当a=1时,曲线y=f(x)与直线y=x-1的位置关系”,从中发现“当x>1时,曲线y=f(x)在直线y=x-1的上方;当0 令g(x)=x-1.观察图像(如图1),命题者发现:当0 f(x2)-f(x1)>g(x2)-g(x1). 为了证明此不等式,可把问题转化为证明不等式 f(x2)-g(x2)>f(x1)-g(x1), 可以构造函数h(x)=f(x)-g(x),证明“当x>1时,h(x)的最小值[h(x)]min”恒大于“当0 此问题的难度不大,不足以压轴.因此,命题者再次进行试题变形. 本题的命题思路是:通过比较自变量x在直线x=1两侧时,函数f(x)的函数值与其切线对应函数值的大小,从而构造出待证不等式.基于此,命题者从各个角度进行编制尝试. 实际上,当1 f(x)>g(x)>0, f(x-1) 从而可构造不等式 f(x)-f(x-1)>g(x)-g(x-1), 即[(x+1)lnx-(x-1)]-[xln(x-1)-(x-2)]>(x-1)-(x-2). 也可以进行如下变形:当1 f(x)>g(x)>0, 可得 (x+1)lnx-(x-1)>x-1, 即 (x+1)lnx>2(x-1), 从而 当0 f(x-1) 可得 xln(x-1)-(x-2) 即 由式(1)和式(2)可构造不等式 此不等式即为题目的待证不等式. 至此我们探究出此类试题的命题思想:以直代曲和比较大小. 基于上述试题命题手法的探究,笔者谈谈如何运用此方法进行试题的命制. 图2 笔者拟构造一个拐点在原点、单调递增,且与直线y=x相切的函数f(x).根据设想,可知所设定的函数需满足f(0)=0,f′(0)=1,f″(0)=0.现设定f″(x)=(x+1)ex-1,则 f′(x)=xex-x+1, 作出函数f(x)的图像,并作出曲线y=f(x)在原点处的切线y=x,其图像如图2所示.第1)小题拟在题干中引入参数,以“曲线y=f(x)在原点处的切线y=x”为条件,求解参数的值;第2)小题拟在第1)小题的前提下,基于研究函数的图像,根据图像的特征提炼不等关系,设置问题.经过反复推敲、琢磨,成题如下. 1)若函数f(x)的图像与直线y=x相切,求实数a的值; 分析1)设切点为(x0,f(x0)),由已知可得 f′(x)=xex-ax+1, 依题意可得 (4) 由式(3)和式(4)得x0=0,a=1或x0=2,a=e2,即a=1或a=e2. 2)因为a g′(x)=x(ex-1). 当x>0时,ex-1>0,g′(x)>0;当x<0时,ex-1<0,g′(x)>0.故当x∈R时,g′(x)≥0,g(x)单调递增.又g(0)=0,从而当0 亦即 (5) 由0 从而 g(-x)<0, 即 得 (6) 由式(5)和式(6)得 即原不等式成立. 我们运用“以直代曲”的手法命制了例2,通过同样的手法,可以得到下述的例3.例3的命题过程不再赘述,试题及其解答一并展示如下,供读者赏析.有兴趣的读者可以尝试推演笔者的命题心路,学习命题方法. 例3已知函数f(x)=ex-1-xlnx-x+1. 1)当a≤-1时,证明:关于x的方程f(x)=ax+1-a有且只有一个实根; 2)当0 分析1)令F(x)=f(x)-(ax+1-a)= ex-1-xlnx-(a+1)x+a, 得 F(1)=0,F′(x)=ex-1-lnx-a-2. 下面证明:ex≥x+1.令h(x)=ex-(x+1),则 h′(x)=ex-1. 由h′(x)=0得x=0,当x∈(-∞,0)时,h′(x)<0;当x∈(0,+∞)时,h′(x)>0,则h(x)在(-∞,0]上单调递减,在[0,+∞)上单调递增,故h(x)的最小值为h(0)=0,因此 ex≥x+1. 对上述不等式变形可得 ex+1≥x, 即 lnx≤x-1, 因此当a≤-1时, F′(x)= ex-1-lnx-a-2≥ x-(x-1)-a-2≥-a-1≥0, 故F(x)单调递增,且F(1)=0,此时F(x)在定义域内有一个零点,即原方程有一个根. 2)由第1)小题可知,当a=-1时, F(x)=f(x)-(ax+1-a)=ex-1-xlnx-1, F(x)在(0,+∞)上单调递增,又F(1)=0,从而当0 ex-1-1 则 又1 ex-1>(x+1)ln(x+1)>0, 则 故 [1] 中华人民共和国教育部.普通高中数学课程标准[M].北京:人民教育出版社,2003. [2] 杨苍洲.2015年高考湖北文科卷压轴试题的命题手法探究[J].中学生理科应试,2017(4):2-3. 2017-07-05 杨苍洲(1979-),男,福建泉州人,中学一级教师.研究方向:数学教育. O122 A 1003 - 6407(2017)11-27-03
2 命题手法探究
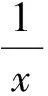
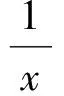
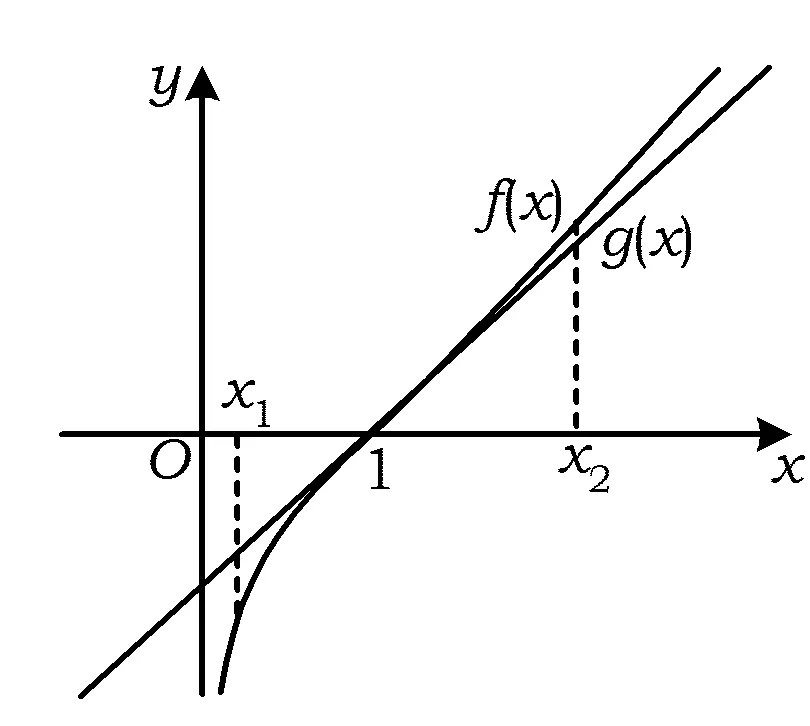
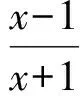
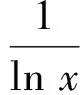
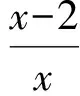
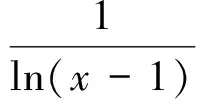
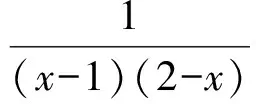
3 基于此手法的试题命制