一类绝对值函数的性质及应用举隅

安徽省无为县牛埠中学(238351) 朱小扣

一类绝对值函数的性质及应用举隅

安徽省无为县牛埠中学(238351) 朱小扣

高考和竞赛中对绝对值的考察一直是重点,学生做这些题目时时常会觉得很难,无从下手,即使做出来耗时也会比较多.针对这一情况,本文将阐述绝对值函数的两条重要的性质,以期在绝对值问题上给大家有所帮助与启发.

绝对值函数的两个性质如下:

性质1 含单绝对值函数f(x)=a|x−b|的图像是“三点两线”,

双绝对值函数f(x)=a1|x−b1|+a2|x−b2|的图像是“四点三线”,

三绝对值函数f(x)=a1|x−b1|+a2|x−b2|+a3|x−b3|的图像是“五点四线”...

性质2 若f(x)=|x−b1|+|x−b2|+···+|x−bn|,则当x是b1,b2,...,bn的中位数时,f(x)最小.

性质1的直接运用

例1(2012年“北约”)求x的范围,使f(x)=|x+2|+|x|+|x−1|是增函数.

解 由性质1可知f(x)图像是“五点四线”,画出图可知x∈[0,+∞)时,f(x)是增函数.(注:五点依次令x=−2,0,1得到三点,再在x＜−2和x＞1各取一点)

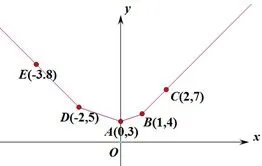
图1

性质1的运用升级

例2(2014年湖北高考理科)已知函数f(x)是定义在R上的奇函数,当x≥0时,若∀x∈R,f(x−1)≥f(x),则实数a的取值范围为__________.

解 可以用四点三线快速地画出f(x)(x≥0)的图像(其中四点分别为O(0,0),A(a2,−a2),B(2a2,−a2),C(3a2,0)),由奇函数的性质得到x＜0的另一半图像,如图,因为对任意实数x都有,f(x−1)≤f(x),即f(x−1)的图像要在f(x)的下方,将C平移到C′′,C′′必须超过C才可以,3a2−(−3a2)≤1解得

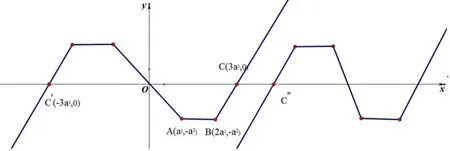
图2

例3(14年福建高考文科12题)在平面直角坐标系中,两点P1(x1,y1),P(x2,y2)间的“L-距离”定义为

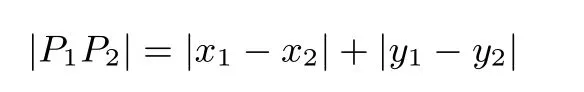
则平面内与x轴上两个不同的定点的“L-距离”之和等于定值(大于|F1F2|)的点的轨迹可以是( )

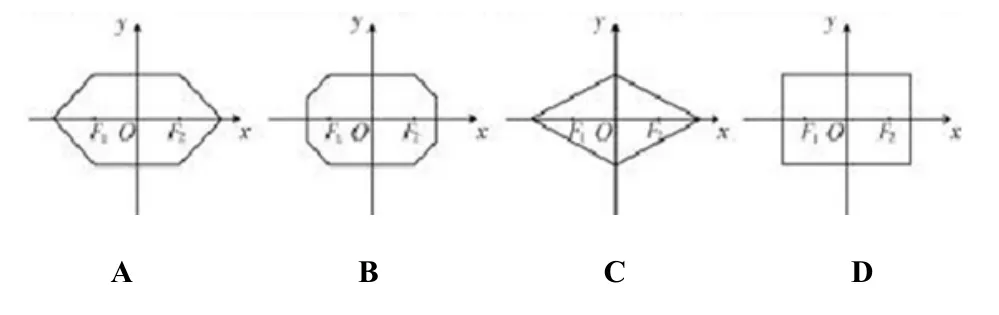
解 不妨设F1(−a,0),F(a,0),其中a＞0,点P(x,y)是其轨迹上的点,且P与x轴上两个不同的定点F1,F2的“L-距离”之和等于定值b(大于|F1F2|).

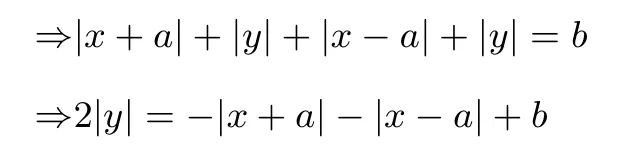
显然图像关于x轴对称,当y≥0时,

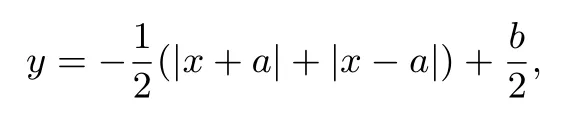
由性质1知图像是“四点三线”,易得答案为A.

点评 三个例题很好的验证了性质1的重要性,特别是例2,例3,如果不会性质1的话,用分类讨论的话,学生很难短时间内画出绝对值函数的图像,在考试时可能会耗时较多,甚至会影响其他题的得分.性质1虽然简单,但会用的人却不多,它不应被老师和同学们忽视,并不是所有的题目都用很复杂的方法去解,实际上,解题往往是”大道至简”.

性质2的直接应用

例4(2016年陕西高中数学联赛初赛)设x∈R,则函数f(x)=|2x−1|+|3x−2|+|4x−3|+|5x−4|的最小值是___.

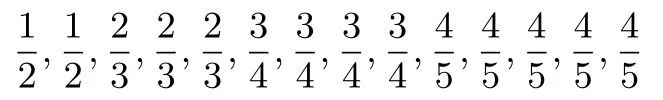
性质2的变式应用

A.0 B.1 C.2 D.3

解法1令

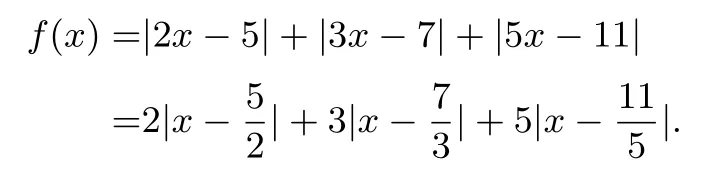
因为

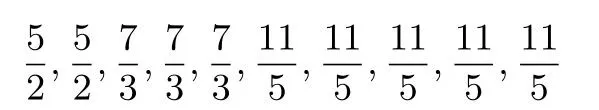
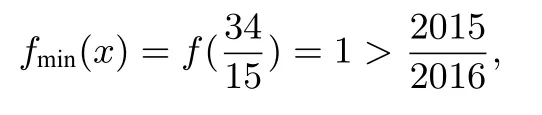
故原方程无解

解法2 令f(x)=|2x−5|+|3x−7|+|5x−11|,易知三绝对值函数图象是:“五点四线”

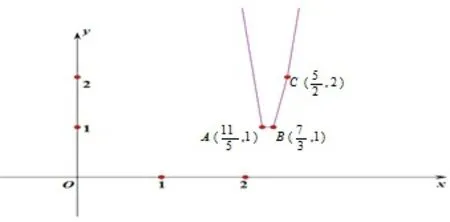
图3

例6(2011年“北约”)求|x−1|+|2x−1|+|3x−1|+···+|2011x−1|的最小值.

解 令

f(x)=|x−1|+|2x−1|+|3x−1|+···+|2011x−1|.则可以求得

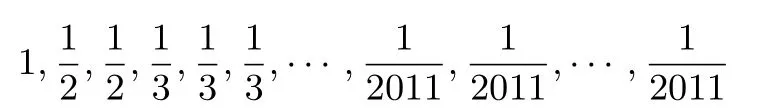
性质2在二元函数中的应用

例7(第五届世界数学团体竞标赛青年组)已知二元函数F(x,y)=|x−1|+|x−2|+|x−3|+|x−4|+|y−1|+|y−2|+|y−3|,求F(x,y)的最小值.

解 令

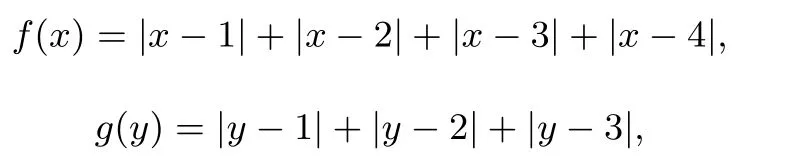
则F(x,y)=f(x)+g(y),由性质2得,

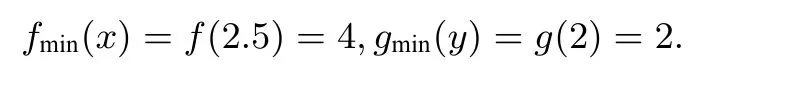
故Fmin(x,y)=fmin(x)+gmin(y)=4+2=6.

性质2在含有变量问题中的应用

例8 (2016年科大自招)对任意的实数x都有|2x−a|+|3x−2a|≥a2,则a的取值范围是___.

解 令f(x)=|2x−a|+|3x−2a|,则只需fmin(x)≥a2即可.注意到

性质2在含有变量问题中的应用引申

例9(“合作杯”试题)m∈R,若方程2|x−1|+3|mx−5|=6无实数解,求m的范围.

解 令f(x)=2|x−1|+3|mx−5|,则只需fmin(x)＞6即可.

(1)当m=0时,f(x)=2|x−1|+15＞6恒成立,满足条件.

(2)当m/=0时,无论m为何值,中位数是1或由性质2得,

点评 在高考和竞赛,对性质2的考察,几乎是每年都有,而且是常考常新,像例8到例9一样,我们常常培养了学生“一题多解”的能力,却忽视了培养学生“一解多题”的能力,只要掌握了上述题中绝对值的本质即性质2,我们就能在学习和考试中灵活运用,就可以化难为简,顺利求解.

总结 通过性质1和2能解决很多绝对值函数,但变式题也很多,如果能了解这种问题本质,那么就能够灵活运用.所以要学好数学,我们必须要会举一反三,触类旁通.总而言之,性质1和2是解决绝对值函数问题的两大利器,也是化难为易的桥梁,熟悉这两条性质,就可以秒杀有关绝对值函数的高考和竞赛题.

[1]朱小扣.含有双绝值的不等式的五种解法[J].中学数学研究(华南师范大学版),2016(13),36-37.