双直线弦长公式及其应用

深圳大学数学与统计学院(518060) 关丽娜 曹丽华

双直线弦长公式及其应用

深圳大学数学与统计学院(518060) 关丽娜 曹丽华

顾名思义,双直线弦长公式指的是:给定两条直线l1,l2第三条直线l3与直线l1,l2相交所成两点(假设有两个交点)之间的距离公式.高考不但考查圆锥曲线的弦长公式,它也考查了双直线弦长公式.以下我们先给出与双直线弦长有关的公式,然后举例子讨论了它的应用.最后,类比这些例子,编拟了一道题目.

在平面直角坐标系xOy中,对于一些位置特殊的直线,我们有如下的双直线弦长公式:

引理 设直线l3∶Ax+By+C=0与直线l1∶x+m1y=0、l2∶x+m2y=0(m1/=m2)相交于M,N两点,则有

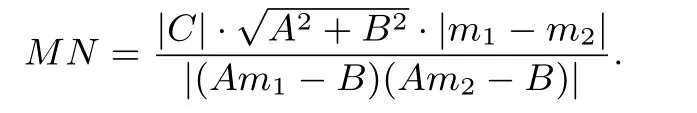
证明 设M,N坐标分别为(x1,y1),(x2,y2).因为A,B不能同时为零,因此不妨设B/=0,则联立

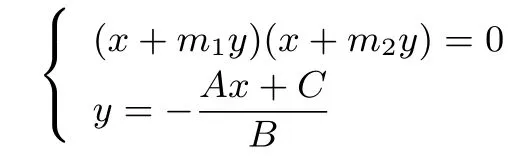
消去y并且整理可得 (Am1−B)(Am2−B)x2+[2Am1m2−B(m1+m2)]Cx+m1m2C2=0.由韦达定理可得

所以

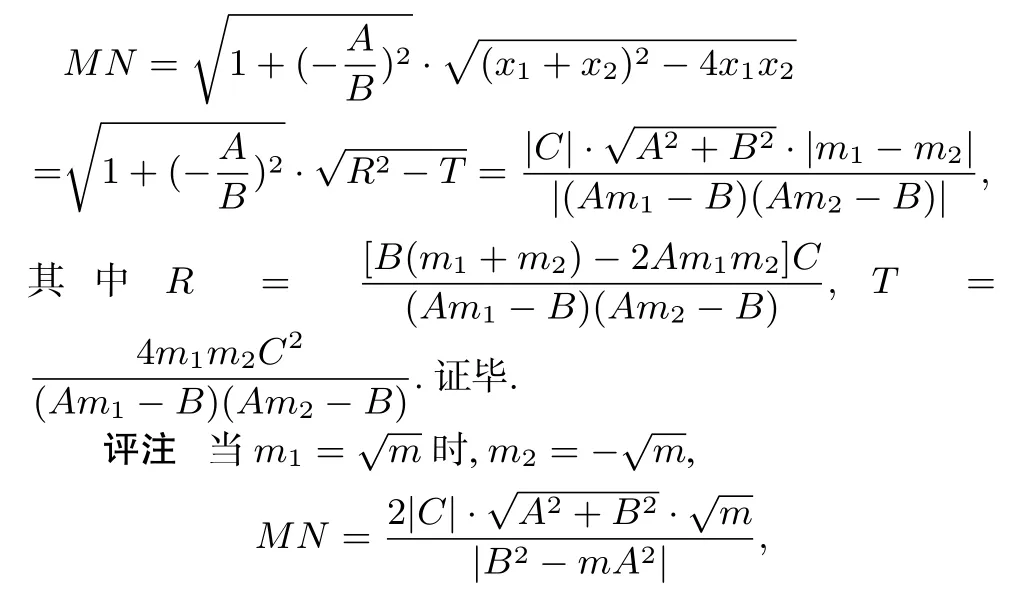
其中m＞0.另外,由于引理要求直线与另外两条直线有两个交点,因此(Am1−B)(Am2−B)/=0,在下面的讨论中就不再重复提起.

有了引理,我们很容易得到以下一个定理:

定理1 设直线l3∶Ax+By+C=0与直线l1∶x+m1y=0、l2∶x+m2y=0(m1/=m2)相交于M,N两点,则有

证明 由点到直线距离公式可得原点到直线l3的距离的方程,若不存在,说明理由.由引理可得

有了这些公式,接下来我们讨论它们在高考数学压轴题中的应用.

(1)求双曲线E的离心率;

(2)如图1,O为坐标原点,动直线l分别交直线l1,l2于A,B两点(A,B分别在第一、四象限)且△OAB的面积恒为8,试探究:是否存在总与l有且只有一个公共点的双曲线E:若存在,求出双曲线E

由引理中的评注,可得

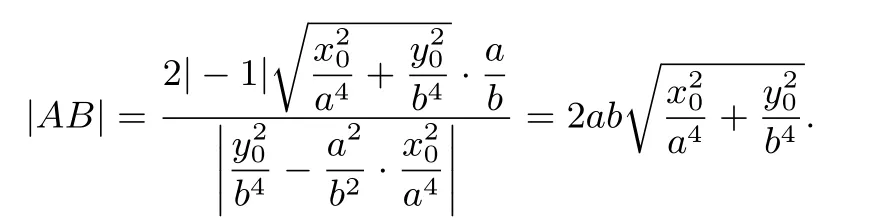
例2(2015湖北)设动直线l与两定直线l1∶x−2y=0和l2∶x+2y=0分别交于P,Q两点.若直线l总与椭圆有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.

解 设直线l与椭圆的公共点为(x0,y0),此时直线l的方程为.因为据定理1的评注得易知在和上单调递增;在和上单调递减;又因为当x0=0或者x0=±4时,S△OPQ=8.故△OPQ的面积的最小值为8.

基于这两道题目的这些特征,笔者编拟了以下一个类似问题以供大家参考讨论.

解 设抛物线上除去L的任意一点P的坐标为(x0,y0),由题意可知|y0|∈(1,+∞).因为抛物线过该点的切线方程为则由定理1的评注可得