“截长补短”法应用中所蕴含的“旋转”思想

四川师范大学数学与软件科学学院(610068) 陈 柳

“截长补短”法应用中所蕴含的“旋转”思想

四川师范大学数学与软件科学学院(610068) 陈 柳

截长补短法是解决线段和差问题的主要方法,但在解题时如何去做辅助线仍然是学生的难点.这篇文章探究了旋转思想在和差问题中的应用,将截长补短法用旋转来刻画,总结并提出了蕴含旋转思想的截长补短法的解题模式.使读者能够更加深刻的理解截长补短法,并在运用时能够快速的找准方向.

旋转 截长补短 和差问题

几何是中学数学的一个重要组成部分.不管是几何证明题还是计算题,通常需要做辅助线来帮助解题,而辅助线的做法却是一个难点.在涉及线段的和差问题中,截长补短法是一个通用的方法.本文通过例题来探究了旋转思想在截长补短法做辅助线上的应用,以此帮助学生能够快速而准确找准突破点,深刻地理解截长补短法.

1 “旋转”辅助证明和差关系

例1 如图1,圆O是△ABC的外接圆,并且△ABC是等边三角形,点P是弧AB上的一个动点,求证:PA+PB=PC.

分析 该题要证明的是线段的和差关系,如果能够将两条较短的线段合并为一条线段,再证明该条线段与最长的那条线段相等,那么问题就迎刃而解了,如果该条线段就是最长的那条线段那就更简单了.

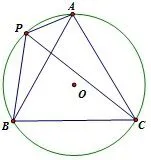
图1

思路一 如果将△ABC绕点A逆时针旋转60°,那么由已知条件、旋转以及圆的知识可以证明,旋转后的三角形为图2中的△ADC,且点P、D、C在同一条直线上,其中有AP=PD,PB=DC,这样就将短的两条线段转移到了长的线段中去,相当于截长补短法中的截长法.

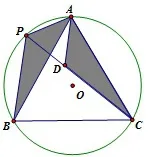
图2

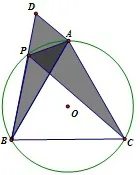
图3

思路二 如果将△APC绕点A顺时针时针旋转60°,那么由已知条件、旋转以及圆的知识可以证明,旋转后的三角形为图3中的△ADB,并且点P、D、B在同一条直线上,其中有AP=DP,DB=PC.相当于截长补短法中的补短法.

证明一 将△APB绕点A逆时针旋转 60°.因为△ABC是等边三角形,则AB旋转后的对应线段为AC.设AP旋转后的对应线段为AD,连接PD,有△APB∼=△ADC.所以AP=AD,又因为 ∠PAD=60°,所以△APD是等边三角形,则PA=PD.由于四边形APBC是圆的内接四边形,有∠APB+∠ACB=180°,所以∠ADC+∠ADP=180°,即点P、D、C在同一条直线上,所以PC=PD+DC=PA+PB.

证明二 将△APC绕点A顺时针时针旋转60°.因为△ABC是等边三角形,则AC旋转后的对应线段为AB.设AP旋转后的对应线段为AD,连接PD,有△ADB∼=△APC.所以AP=AD,又因为 ∠PAD=60°,所以APD是等边三角形,则PA=PD.由于四边形APBC是圆的内接四边形,有∠APB+∠ACB=180°,所以∠APB+∠DPA=180°,即点P、D、B在同一条直线上,所以PC=DB=PD+PB=PA+PB.

解题模式 步骤1:通过观察,将其中一条较短的线段旋转到最长的线段中去(将最长的线段旋转到其中一条较短的线段中去).步骤2:通过有关知识证明长线段中剩余的一部分与另一条短的线段相等(证明旋转后多出的一部分与另一条短的线段相等).

2 以和差关系为已知条件解决相关问题

例2如图4,已知AB=CD=AE=BC+DE=2,∠ABC=∠AED=90°,求五边形ABCDE的面积.

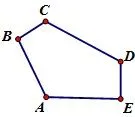
图4

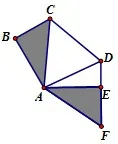
图5

分析 该题是以线段和差问题为条件,求五边形ABCDE的面积.由图可以直观的看到该五边形是一不规则的五边形,求这种图形的面积,可以将该图形分解成所熟知的图形进而求解,也可以将该图形的某一部分进行转移使之形成规则图形进而求解.

由题可知AB=AE,∠ABC= ∠AED=90°,如果将△ABC顺时针旋转∠EAB,AB刚好与AE重合,并且点D、E、F在同一直线上,这样就将五边形的面积转移到△AFD和△ACD的面积之和.再由已知条件可以轻松的证明△ACD∼=△AFD,并能求出△AFD的面积,进而求出五边形的面积.

解 如图5,将△ABC顺时针旋转 ∠EAB,因为AB=AE,所以旋转后的图形为△AEF,连AD.因为∠ABC=∠AED=90°,所以点D、E、F在同一直线上.在△ACD与△AFD中,因为AC=AF,

3 “旋转”探究线段之间的数量关系

例3 在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.

探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系.

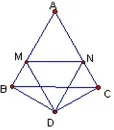
图6

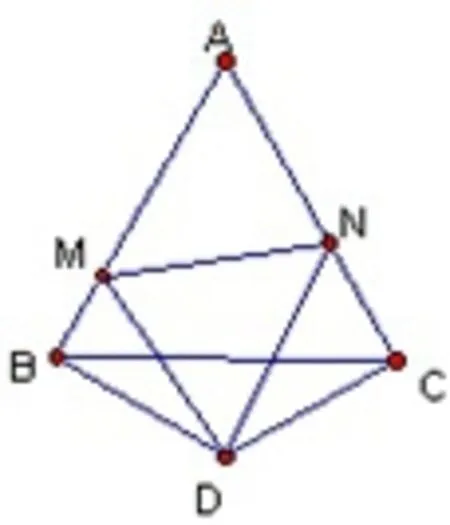
图7

(1)如图6,当点M、N在AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是?

(2)如图7,点M、N在AB、AC上,且当DM/=DN时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明.

分析 (1)可大胆猜测MN=BM+CN,此时思路就是把BM、NC转移到一条直线上.由题义可知BD=DC,由已知易得 ∠MBD= ∠NCD=90°,可将△MBD绕点D顺时针旋转120°得到△M1CD,如图.易证△NDM∼=△NDM1,则NM=NC+CM1=NC+BM.

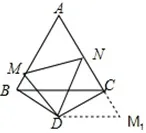
图8

(2)同第一题的分析.

解 (1)∠BDC=120°,BD=DC,所以 ∠DBC=∠DCB=30°,已知△ABC是等边三角形,所以∠MBD=∠NCD=90°.又因

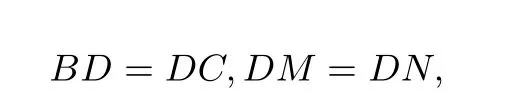
所以Rt△BDM∼=Rt△CDN,已知 ∠MDN=60°,所以 ∠MDB= ∠NDC=30°.将△MBD绕点D顺时针旋转 120°得到△M1CD,△MBD∼=△M1CD.由于∠NCD+∠MCD=180°,所以点N、C、M1在同一条直线上.因为

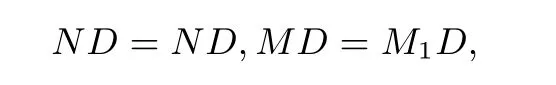
且

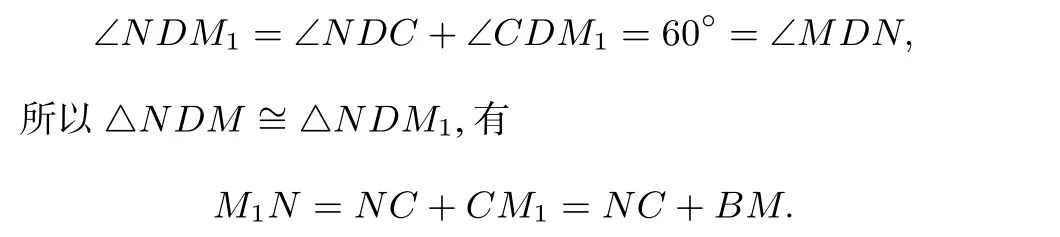
(2)猜想:结论仍然成立.

证明 同(1)证明.

说明:不管MD与ND是否相等,都有

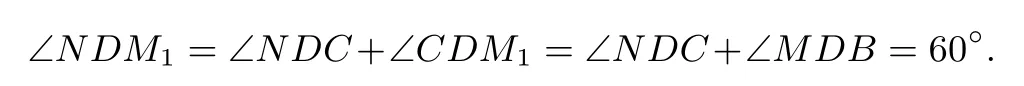
这篇文章主要探究了截长补短法在解决线段的和差问题时所蕴含的旋转思想,换句话说就是旋转在解决线段和差问题的运用,并给出了有关问题的解题模式.在解决某些线段和差问题时,利用旋转可以使解题过程更加简明清晰,不必去繁琐证明线段相等,图形全等,如例1中DC=PB,PC=DB,可由旋转性质直接得到.探究旋转在线段和差问题中运用,是为了深化截长补短法.解决线段的和差问题整个的大思想还是截长补短,但是旋转可以使截长补短的这个过程更加的简单清晰.特别针对旋转很熟悉的读者,使之对线段和差问题的解决提升一个阶梯.