W.Janous不等式的变式
华南师范大学数学科学学院(510631) 尹倩倩 冯 姗 黄 威
W.Janous不等式的变式
华南师范大学数学科学学院(510631) 尹倩倩 冯 姗 黄 威
我们主要利用排序不等式、柯西不等式及线性变换等方法证明了W.Janous不等式的36个变式中的27个变式,另外9个变式存在反例.
W.Janous不等式 排序不等式 线性变换
一、猜想的提出
W.Janous猜想:设x,y,z>0,则
该猜想最先发表在加拿大《数学难题》杂志1612期上,最后成为数学难题刊登在《数学通讯》1992年第4期上,从此引入国内,引起诸多数学爱好者兴趣,现已有多种证明方法及推广形式.我们从排序不等式证法中受到启发,由文[1]猜想:对分子为x2,y2,z2与xy,yz,zx的全排列所对应的36个变式是否全部成立(其中x,y,z均为正数).下面依据x2,y2,z2的排列方式将36个变式分成六种情形讨论,即:
1.情形一:
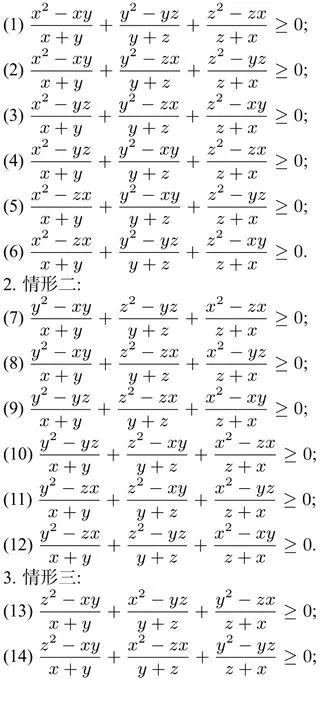

二、引理
(一)引理1[2](排序不等式)设有两组实数a1,a2,...,an和b1,b2,...,bn,满足

则有
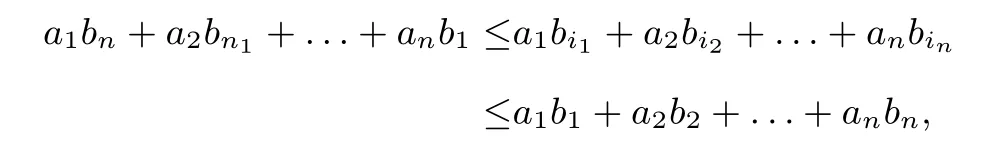
其中i1,...,in是1,...,n的任意排列,等号当且仅当a1=a2=···=an或b1=b2=···=bn时成立.
(二)引理2[3](柯 西 不 等 式)设a1,a2,...,an及b1,b2,...,bn为任意实数,则不等式

成立,当且仅当ai=kbi(i=1,2,...,n)时等号成立.
三、猜想的证明
(一)由排序不等式知,若x≥y≥z,则

从而有(顺序和≥乱序和≥倒序和),即
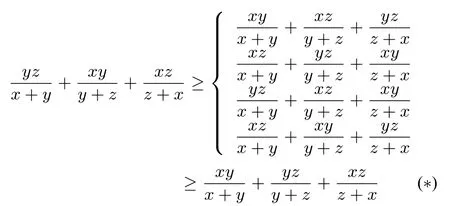
因此,在情形一中,只需要证明变式(4):

成立即可.
证明 由于x,y,z均为正数,原不等式两边同时乘(x+y)(y+z)(z+x),原不等式等价于:

两边同除xyz,

事实上,由柯西不等式知

由 (∗)式可知:

所以情形一中的全部变式可得证.同理,在情形二中,只需要证明变式(10):
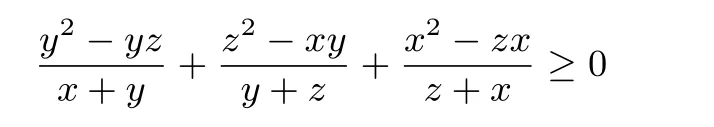
成立即可.
证明 由对偶性知

故由已证得的变式(4):
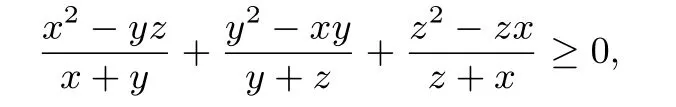
命题可得证.
所以情形二中的全部变式可得证.同样地,在情形三中,只需要证明变式(16):
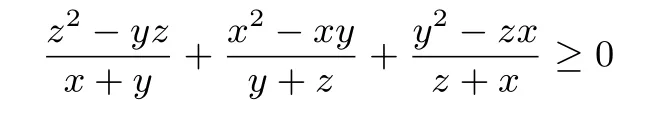
成立即可.
证明 由W.Janous不等式
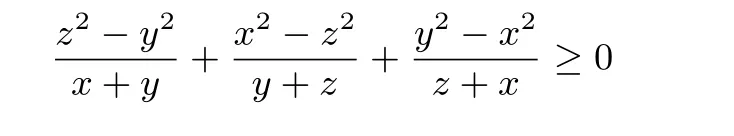
知

由上述已证的变式(10)知

故

所以情形三中的全部变式可得证.
综上,由排序不等式、对偶性可以容易证得前三种情形的变式均成立.然而,观察情形四、五、六中的不等式的结构可知,它们无法由排序不等式统一证明,故我们需要另辟蹊径.
(二)下面利用柯西不等式与均值不等式,证明变式(19):
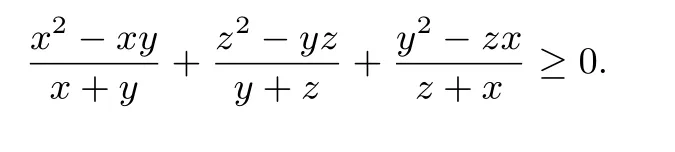
证明 由于x,y,z均为正数,根据柯西不等式可知,
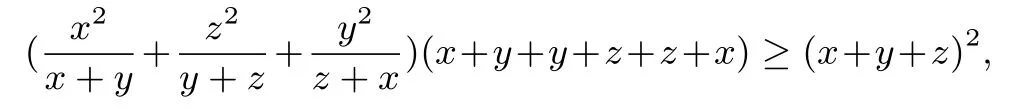
即

又由均值不等式知
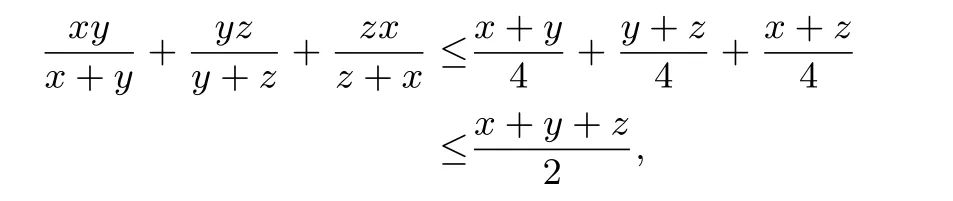
故

即

同理,可证得变式(25):

(三)下面利用换元法及函数法,证明变式(20):

证明①当x≤y≤z时,令
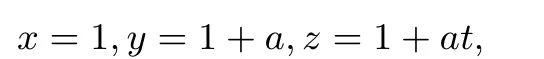
其中a≥0,t≥1.要证

对该式去分母化简,上式等价于

即

即

由于a≥0,t≥1,令
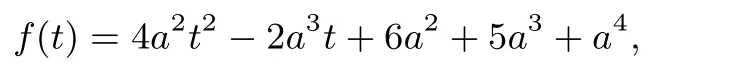
则

故

所以(a)式显然成立.
②当x≤z≤y时,令

其中a≥0,t≥1.要证

对该式去分母化简,上式等价于

即

令

则

因为a≥0,t≥1 所以f′(t)=24a4t+30a3≥0,所以f′′(t)单调递增,

所以f′(t)单调递增,

所以f′(t)单调递增,

所以f(t)单调递增,

所以(b)式显然成立.
③当y≤z≤x时,令
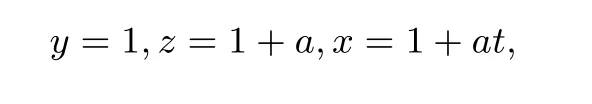
其中a≥0,t≥1.要证

对该式去分母化简,上式等价于

由于a≥0,t≥1,故(c)式显然成立.
④当y≤x≤z时,令

其中a≥0,t≥1.要证
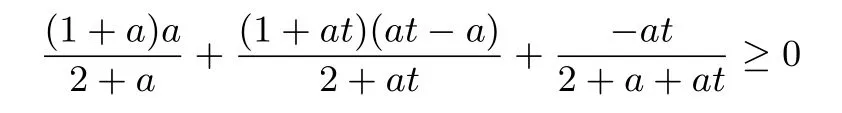
去分母化简,上式等价于

由于a≥0,t≥1故(d)式显然成立.
⑤当z≤x≤y时,令
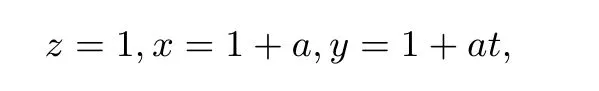
其中a≥0,t≥1.要证

对该式去分母化简,上式等价于

即

由于a≥0,t≥1故(e)式显然成立.
⑥当z≤y≤x时,令
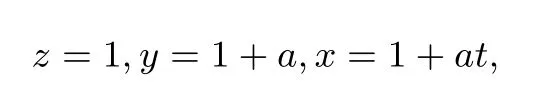
其中a≥0,t≥1.要证

对该式去分母化简,上式等价于

即
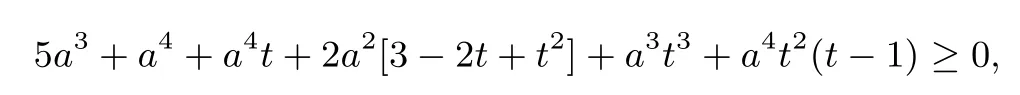
即
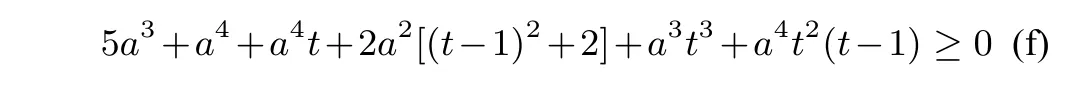
由于a≥0,t≥1故(f)式显然成立.
综上,对任意正数x,y,z,均有
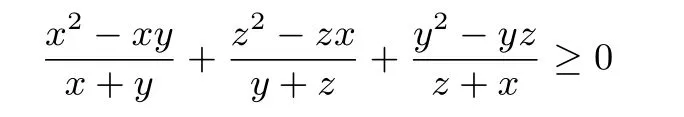
成立.
将变式(20)中的x,y,z进行轮换变换后,不等式仍成立,即,
令x→y→z→x,可得变式(28):
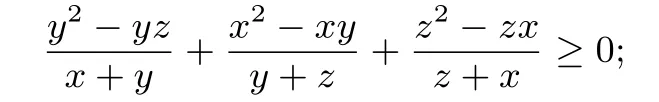
令x→z→y→x,可得变式(36):
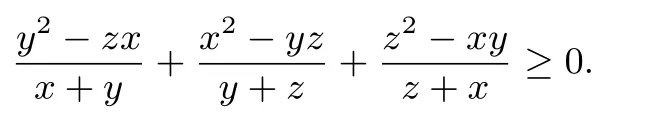
用变式(20)的方法易证,变式(24):

同样将变式(24)中的x,y,z进行轮换变换;
令x→z→y→x,可得变式(26):

令x→y→z→x可得变式(34):
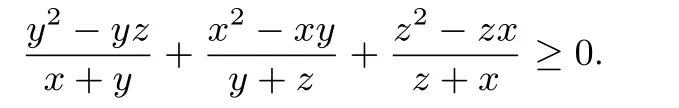
综上,我们主要利用排序不等式、线性变换,加上柯西不等式、均值不等式、对偶法、换元法、函数法等方法证明了36个变式中的27个变式是成立的.而剩下9个变式是不成立的,通过变式(20)的证明方法及线性变换,都可以找到对应的反例.
四、反例
反例1变式(23):

不成立.事实上,当z≤y≤x时,不妨设x=1+at,y=1+a,z=1,其中a≥0,t≥1.只需证

化简后等价于

则
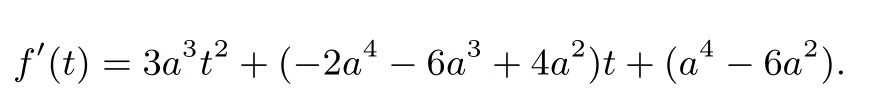
则
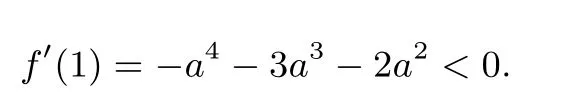
容易验证当t≥1时,恒有f′(t)<0.因此,当t≥1时,f(t)单调递减.而

易知当a∈(0,2)时,f(2)>0;当a∈(2,+∞)时,f(2)<0.不妨令a=3,t=2,此时x=7,y=4,z=1,则

下面将反例1中的参数x,y,z进行下列线性变换,可得以下结果:令x↔z,y↔y,即当x=1,y=4,z=7时,有
令x↔y,z↔z,即当x=4,y=7,z=1时,有
令x↔x,y↔z,即当x=7,y=1,z=4时,有
令x→z→y→x,即当x=4,y=1,z=7时,有
令x→y→z→x,即当x=1,y=7,z=4时,有
同理,类似反例1,根据变式(20)的方法我们同样可以找到变式(22)的反例:
事实上,令x=3,y=2,z=1,故
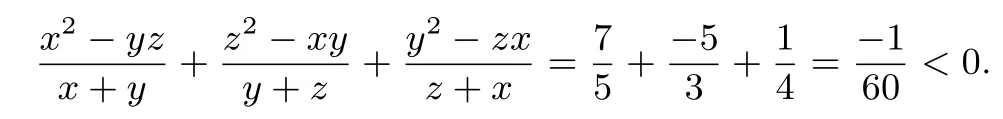
再将反例7中的参数x,y,z进行下列线性变换,可得以下结果:
令x↔y,z↔z,即当x=2,y=3,z=1时,有
令x↔x,y↔z,即当x=3,y=1,z=2时,有
注 容易验证反例7中的参数x,y,z的另外三种线性变换的结果和反例7、8、9对应的变式相同.
综上,9个反例均已找到,即变式(21)(22)(23)(27)(29)(30)(32)(33)(35)均不成立.
[1]曹嘉兴.W.Janous猜想的变式[J].中学数学研究,2013(8):47.
[2]苏农,刘玲.关于排序不等式的一个简单证明[J].高等数学研究,2011(14):49-50.
[3]丘维声.高等代数(上册)[M].北京:高等教育出版社,1996.
[4]田洪,滕曙霞.对称式•循环对称式•排序法-由W.Janous猜想得到的[J].数学教学通讯,2000(7):29-30.

