例谈解析几何中的多动点最值问题的求解

甘肃省康乐县康乐中学 齐斌德

例谈解析几何中的多动点最值问题的求解

甘肃省康乐县康乐中学 齐斌德

解析几何是高中数学中的重要知识点,是“数形结合”这一数学思想方法的集中体现,圆锥曲线中的一些最值问题是近几年高考中的热点,而其中的多动点问题,由于动点多,导致涉及面加大,如果不掌握一些方法,往往在纷繁复杂的情况下理不出头绪来.所谓“多动点”问题,就是题目中的动点不止一个,而是有多个,某一动点运动时会带动或制约其他一些点的运动,在这种错综复杂的情况下,会有一种“山重水复疑无路”的感觉,但是我们如果能够尽可能地使动点的数目减少,往往就会出现“柳暗花明又一村”的局面.现就这种情况下求最值问题谈一些方法.

一、动点转化为定点

例1已知点P是抛物线y2=2x上的动点,点P到准线的距离为d,且点P在y轴上的射影是M,点则

|PA|+|PM|的最小值是()

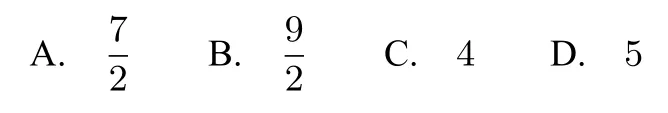
分析 本问题的实质是求折线段APM的最小值,而在这个问题中有P、M两个点在同时运动,给解决问题带来了一定的困难,如果能够将其中的一个动点转化为定点,则会使问题变得简单.考虑到抛物线的焦点F为一个定点以及抛物线的定义,可以尝试着将动点M朝着定点F转化,这样就可以将原来问题中的两个动点转化为一个动点,从而使问题得以解决.

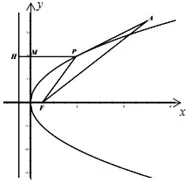
图1

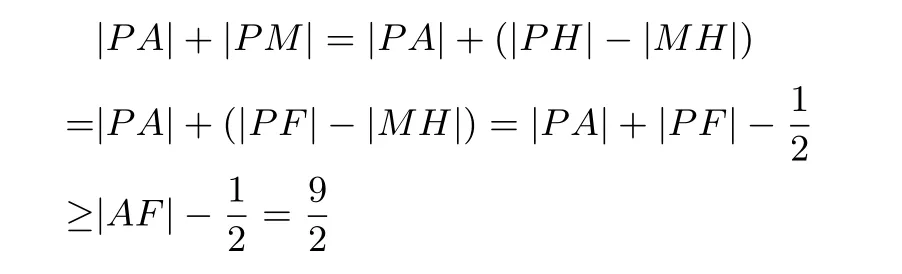
(当且仅当A、P、F三点共线时取等号),因此|PA|+|PM|的最小值为因此选择B.

例2 若点P在抛物线y2=x上,点Q在圆C∶(x−3)2+y2=1上,则|PQ|的最小值为____.

分析 该问题所求的是P、Q两点之间距离的最小值,但是由于P、Q两点都是动点,给解决问题带来了困难,但是考虑到抛物线的焦点和圆C的圆心是定点,圆C的半径为定值,如果能够将两个动点中的一个和上述的定点和定值建立联系,就会使问题变得简单.

解 如图2,

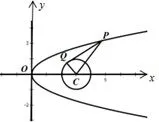
图2

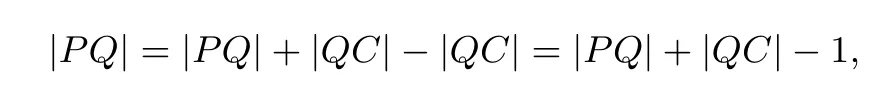
欲求|PQ|的最小值,只需要求|PQ|+|QC|的最小值即可,而|PQ|+|QC|≥|PC|(当且仅当P、Q、C三点共线时取等号),的|PC|最小值即为|PQ|+|QC|的最小值.设P(x0,y0),则

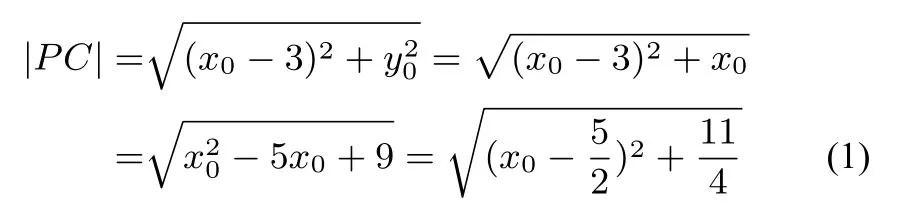
(x0≥0),易知此时|PQ|取得最小值

例3(2015年湖南卷)已知点A、B、C在圆x2+y2=1上运动,且AB⊥BC.若点P的坐标为(2,0),则的最大值为()

A.6 B.7 C.8 D.9

图3

解 如图3,

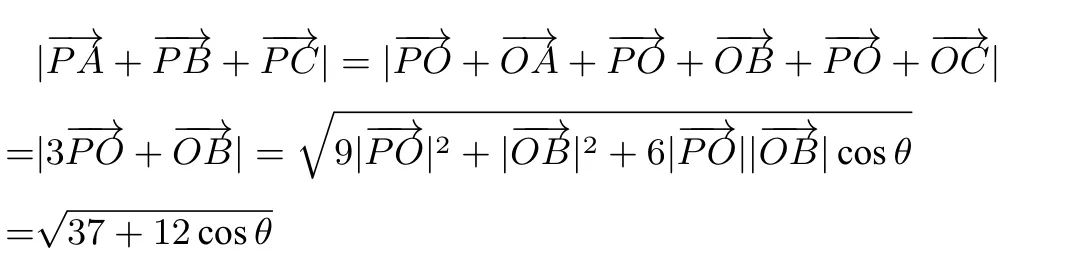
当cosθ=1即θ=0时,上式取得最大值7.

二、固定部分动点

例4设P是圆(x−3)2+(y+1)2=4上的动点,Q是直线x=−3上的动点,如图4,则|PQ|的最小值为_______.

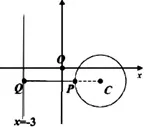
图4

分析 该问题所求的是P、Q两点之间距离的最小值,但是由于P、Q两点都是动点,给解决问题带来了困难,这时可以考虑将其中的一个动点固定.

解 不妨将点Q固定,则问题转化为求圆C外一定点Q到圆C上的点P的距离最小的问题.显然,当C、P、Q三点共线时,

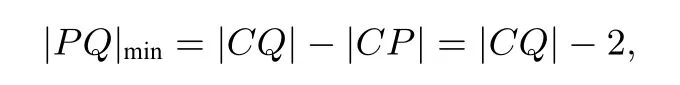
所以当|CQ|最小时,|PQ|也最小.问题转化为求圆心C到直线上的动点Q的最小值问题,易知当CQ与直线x=−3垂直时,|CQ|min=6,所以|PQ|min=6−2=4.

再来看例2,如图5,同样是求P、Q两点之间距离的最小值,但是由于P、Q两点都是动点,可以考虑将其中的一个动点固定.不妨将点P固定,则问题转化为求圆C外一定点P到圆C上的点Q的距离最小的问题.显然,当C、P、Q三点共线时,

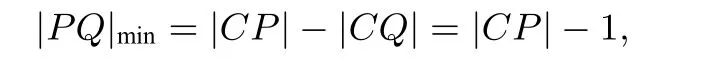
所以当|CP|最小时,|PQ|也最小.问题转化为求圆心C到抛物线y2=x上的动点P的最小值问题,设P(x0,y0),由(1)式易得,此时|PQ|取得最小值

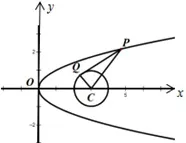
图5

三、构造新定点

例5已知P是圆(x−2)2+y2=1上的动点,Q是y轴上的动点,A(1,2)为定点,求|AQ|+|QP|的最小值.

分析 本题实质上是求折线段AQP的最小值,因此解决本题的关键是化折为直,而目前的条件下很难实现这一目标.实质上,我们只要对A作对称变换,找到一个新的定点,就可以将折线段化为直线段.

解 如图6,作点A关于y轴对称的点A′,则|A′Q|=|AQ|,从而

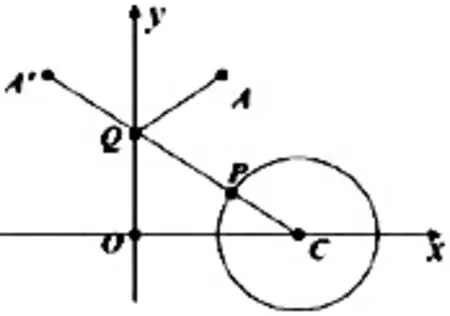
图6

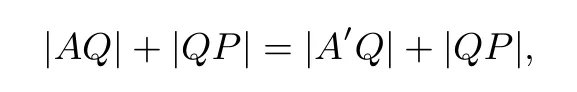
问题转化为求折线段A′QP的最小值,显然,当A′QP是直线段时长度最小,问题转化为求圆C上的一个动点P到圆外一定点A′的最短距离,由圆的性质可知当P、C、A′三点共线时,|A′P|最小,最小值为 =|A′C|−|CP|,所以

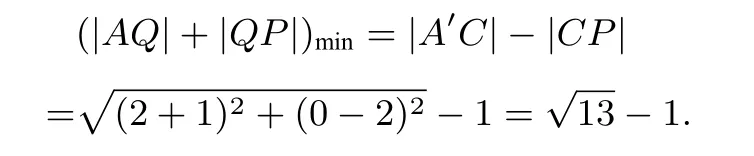
解析几何不但强调用代数的方法研究几何问题,还强调用“几何要素”来引导代数形式的运算和证明.解析几何中类似以上的多动点问题是学生在学习中的难点,在实际的问题解决中,可以结合题目中的信息画出对应的图像,结合图形的一些特征,寻找题目中动的量与静的量之间的联系,化动为静,变多动点问题为单动点问题,从而解决相应的问题.