追本溯源明本质 引申探究点差法

浙江省杭州市富阳区新登中学(311404) 汪道智

追本溯源明本质 引申探究点差法

浙江省杭州市富阳区新登中学(311404) 汪道智

点差法是解决圆锥曲线中点弦问题的一种基本方法,而学生对点差法的掌握往往只停留在问题表面的一种记忆性的结论,而没有理解问题的本质.本文对点差法进行了一些探究与引申,以帮助学生理解圆锥曲线中点弦问题的本质,提高解题能力.

圆锥曲线 中点弦 点差法

1.原题呈现

题目 (人教A版高中数学选修2-1第49页习题2.2 A组第8题)已知椭圆,一组平行直线的斜率是

(1)这组直线何时与椭圆相交?

(2)当它们与椭圆相交时,证明这些直线被椭圆截得的线段的中点在一条直线上.

解 (1)略.(2)点差法 设直线被椭圆截得的线段两端点分别为A(x1,y1),B(x2,y2),AB的中点为M(x,y).则

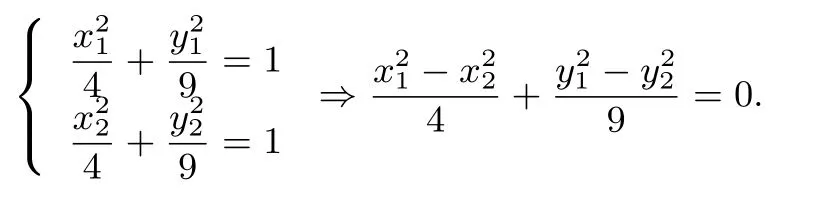
所以

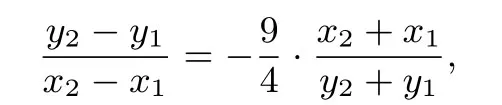
笔者将在下文中对点差法进行一些引申与探究,以期能对通过此文帮助学生加深对圆锥曲线中点弦问题的本质的理解.

2.基本模型

首先以焦点在x轴上的椭圆为例:如图1不过原点O的直线l与椭圆(a＞b＞0)交椭圆于A、B两点,M为线段AB的中点,则(其中e为椭圆的离心率).

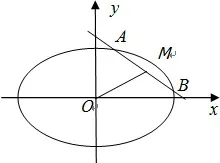
图1

简证 设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0).则

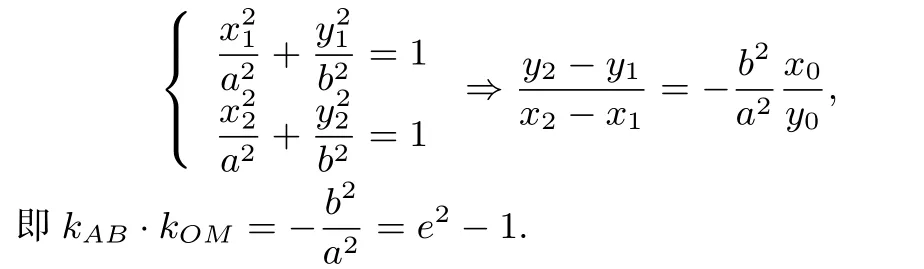
变式 (1)焦点在y轴上的椭圆则

(2)焦点在x轴上的双曲线则kAB·kOM=

(3)焦点在y轴上的双曲线则

以上几个圆锥曲线中点弦性质均可以用点差法证明,这里不再赘述.下面继续探究与上述性质相关的一些问题.

3.性质探究

下面对焦点在x轴上的圆锥曲线进行探究与引申:

引申1 若A、B是椭圆上关于原点对称的两个点,M是椭圆上不同于A、B的任意一点,则

分析 文[1]中用代数法已给出证明,笔者在这里运用图形阐述引申1的结论与上述中点弦性质之间的联系.如图2,取MB的中点D,由椭圆中点弦性质易得,在△MAB中,OD//MA,所以kOD=kMA,即

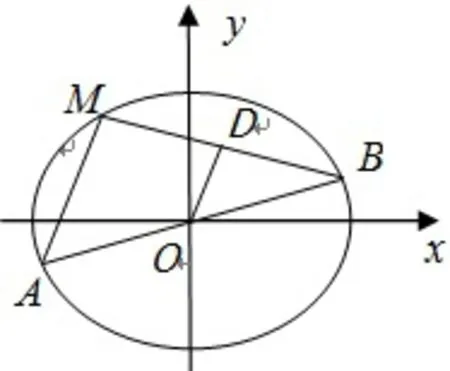
图2

特别地,若A、B是椭圆上长轴的两个端点,M是椭圆上不同于A、B的任意一点,则

反之若A、B是x轴上关于原点对称两个定点,M是不同于A、B的任意一点,若有则点M的轨迹是以A、B为长轴的椭圆.

人教A版数学选修2-1第41页例3就是此概念的典例.

引申2 若A、B是双曲线上关于原点对称的两个点,M是双曲线上不同于A、B的任意一点,则反之若A、B是x轴上关于原点对称两个定点,M是不同于A、B的任意一点,若有则点M的轨迹是以A、B为实轴的双曲线.

特别地,若A,B是双曲线实轴轴的两个端点,M是双曲线上不同于A,B的任意一点,则反之若A、B是x轴上关于原点对称两个定点,M是不同于A,B的任意一点,若有则点M的轨迹是A,B为实轴的双曲线.

引申3不过原点O的直线l与双曲线的两条渐近线分别交于A、B两点,M为线段AB的中点,则

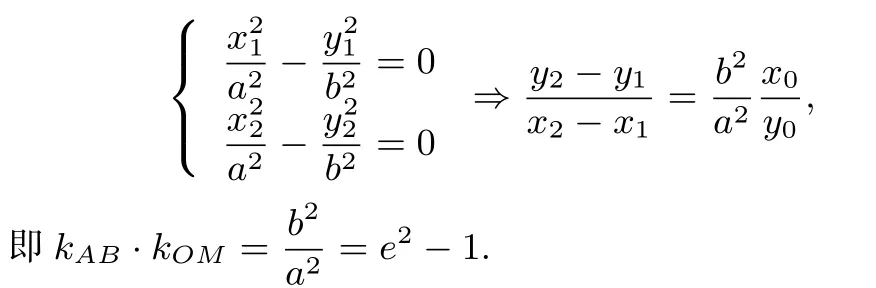
简证 设M(x0,y0),则椭圆在M点处的切线方程为(求解方法可参见[2]),即又,所以

另外我们也可以从极限思想来理解.如图3,当图1中的直线AB平行向右上方移动时,A、B两点无限接近,极限状态是直线AB与椭圆相切,此时中点M演变为切点M,所以

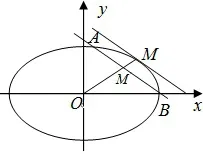
图3

简证 由引申4,

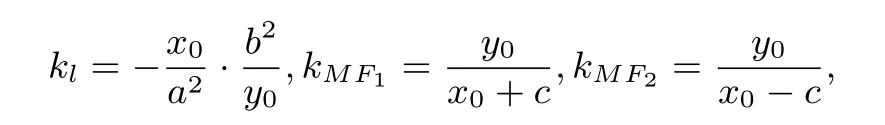
易得,

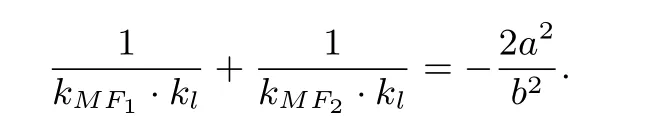
4.解法赏析

圆锥曲线中点弦问题在近几年高考中真题中频繁出现,应用上述性质解题事半功倍.请欣赏:

(1)求实数m的取值范围;

(2)求△AOB面积的最大值(为坐标原点).

解 (1)如图4,设A(x1,y1),B(x2,y2),AB中点M(x0,y0).由点A、B关于直线对称得由得到:

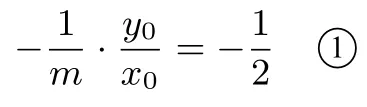
又AB中点M在直线上,

联立1○,2○,得

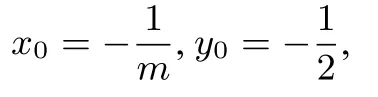
由M(x0,y0)在椭圆内部得到:可解得或

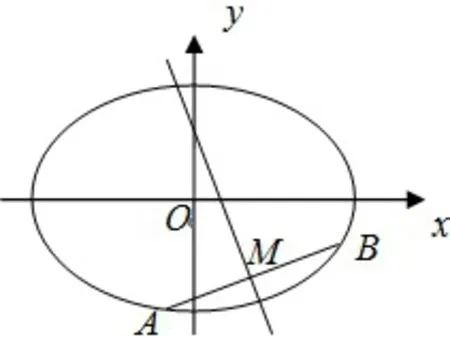
图4

(2)略.

点评 此题也可以设AB方程为通过联立直线与椭圆方程利用判别式和韦达定理来做,但计算量相对较大,容易出现计算错误.而利用中点弦性质,方法简捷明快,很好地激发了学生的解题兴趣.

例2(2014年浙江高考理科第16题)设直线x−3y+m=0(m/=0)与双曲线的两条渐近线分别交于点A、B.若点P(m,0)满足|PA|=|PB|,则该双曲线的离心率是___.

解 设AB中点M(x0,y0),由题意可得方程组

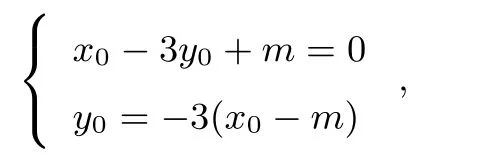
点评 学生解决此题的直观解法是将渐近线方程与已知直线联立方程组,分别解出A、.B两点的坐标,进而得到AB中点M的坐标,再利用kPM·kAB=−1得到关于a,b的一个等量关系求得离心率.显然利用引申3的性质解决此题要方便得多.

(1)求直线y=kx+1被椭圆截得的线段长(用a,k表示);

(2)若任意以A(0,1)为圆心的圆与椭圆至多有三个公共点,求椭圆离心率的取值范围.

解 (1)略;(2)如图5,从问题的反面考虑.假设圆与椭圆的公共点有4个,由对称性可设y轴左侧的椭圆上有两个不同的点P、Q满足|AP|=|AQ|,令PQ中点M(x0,y0).

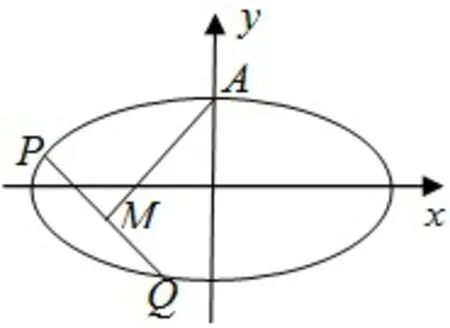
图5

设PQ∶y=kx+b,则由kOM·k=e2−1,得则

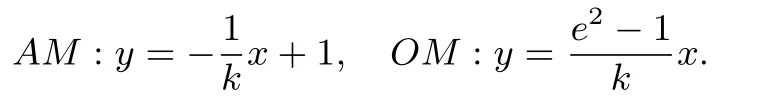
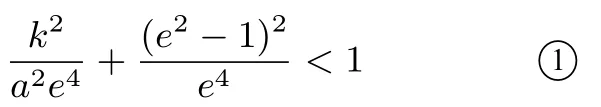
将②式代入①式可得,由存在性知,解得所以椭圆离心率的取值范围是

点评 此题是浙江省高考考查解析几何的一道难度较大的解答题,第二问得分率较低.究其原因还是学生对圆锥曲线中点弦问题的本质理解不够深刻.

5.追本溯源

点差法在教材中虽然没有以例题的形式出现,但它是源于教材习题的“变身”.在教学中教师如果仅仅告诉学生圆锥曲线中点弦问题使用点差法就匆匆而过,实在可惜!在数学上遇到一个真正触及数学灵魂的题目时,我们要停下匆匆的脚步,认真感悟、欣赏,并且能够将数学最本质的东西教给学生.许多高考试题也是课本例题、习题的华丽转型.作为教师要重视对教材的研究,能将课本的例题、习题加以拓展、深化,挖掘数学问题的内涵.高考源于教材而高于教材,教学中需要教师正确理解教材例题设计的意图,发现规律,找到共性,这才是事半功倍的做法.

[1]苏立标.探求以e2−1为定值的圆锥曲线问题[J].中学数学教学,2006(3):18-19.

[2]李红春.椭圆切线方程的两种巧妙求法[J].中学生数学,2014(10)(高中):11.