由一道高考不等式证明题引发的思考

湖南省会同县第一中学(418300) 于先金 黄为公

由一道高考不等式证明题引发的思考

湖南省会同县第一中学(418300) 于先金 黄为公

1.试题呈现

2017 年高考全国II卷文、理科第23题:

已知a＞0,b＞0,a3+b3=2,证明:

(I)(a+b)(a5+b5)≥4;

(II)a+b≤2.

这道试题难度不大,但值得我们去品味,通过对这道试题的探究和反思,得到了一些有意义的结论:一是两个不等式的多种证法,可谓精彩呈现;二是两个不等式的变式与推广,使我们对问题认识得更深刻;三是关于解题教学的一点思考.

2.第(I)问的证法探究

证法1(展开配方,简单明了)因为a＞0,b＞0,a3+b3=2,所以

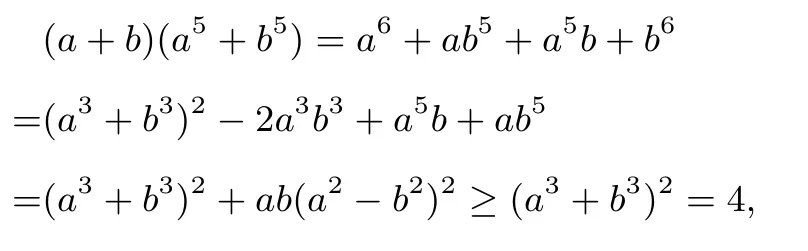
所以(a+b)(a5+b5)≥4.

证法2(柯西登场,马到成功)

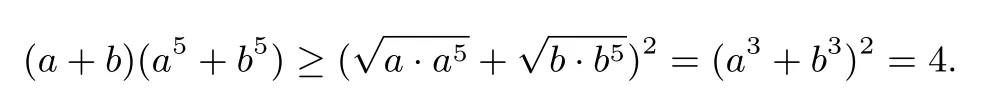
评注 对第(I)问不等式的证明,2017年高考题汇编解析的各种资料,基本上是采用上述两种证法之一,可谓是通法.

证法3(执果索因,柳暗花明)

要证(a+b)(a5+b5)≥4,因为a3+b3=2,所以只需证(a+b)(a5+b5)≥(a3+b3)2,展开得a6+ab5+a5b+b6≥a6+2a3b3+b6,只需证ab5+a5b≥2a3b3.

又a＞0,b＞0故只需证a4+b4≥2a2b2,即证(a2−b2)2≥0上式显然成立,故原不等式成立.

证法4(均值换元,别出心裁)因为a＞0,b＞0,a3+b3=2,不妨设a≤b,所以可令a3=1−x,b3=1+x,

其中0≤x＜1.于是

所以(a+b)(a5+b5)≥4.

当a=b时,f(x)=b为常数函数;当a＞b时,有a−b＞0,是减函数,从而是增函数,所以f(x)是增函数;当a＜b时,有a−b＜0,是增函数,从而是增函数,所以f(x)是增函数.

综上可知,当x1＜x2时,恒有f(x1)≤f(x2),等号当且仅当a=b时成立.所以有f(4)≥f(3)≥f(2)≥f(1),即

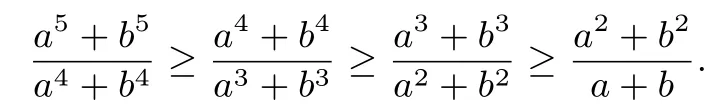
所以(a+b)(a5+b5)≥(a2+b2)(a4+b4)≥(a3+b3)2=4.

3.第(I)问的变式和推广探究

变式1(改变结论)已知a＞0,b＞0,a3+b3=2.

证明 (1)(a2+b2)(a5+b5)≥2(a4+b4);(2)2(a+b)≥(a2+b2)2;(3)(a2+b2)(a4+b4)≥4等.

变式2(改变条件)已知a＞0,b＞0,a2+b2=2

证明 (1)(a+b)(a3+b3)≥4;(2)(a3+b3)(a5+b5)≥4等.

推广 若a＞0,b＞0,且m＞n则(am+1+bm+1)(an+bn)≥(an+1+bn+1)(am+bm)

变式与推广,由证法5中函数f(x)的单调易证,在此从略.

4.第(II)问的证法探究

4.1 用综合法证明

证法1 由因导果均值放缩由a3+b3= 2得(a+b)(a2−ab+b2)=2,从而(a+b)[(a+b)2−3ab]=2.

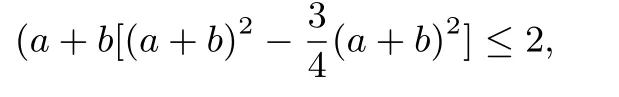
所以(a+b)3≤8,故a+b≤2.

证法2(立方公式均值放缩)

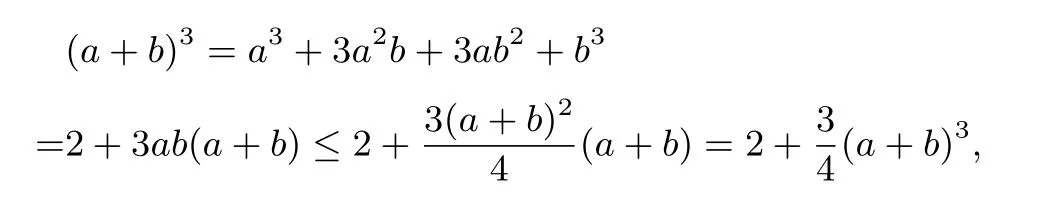
所以(a+b)3≤8,故a+b≤2.

评注 对第(II)问的证明,这两种方法也是通法.证法3(由因导果,顺流而下)由已知可得从而ab≤1.所以

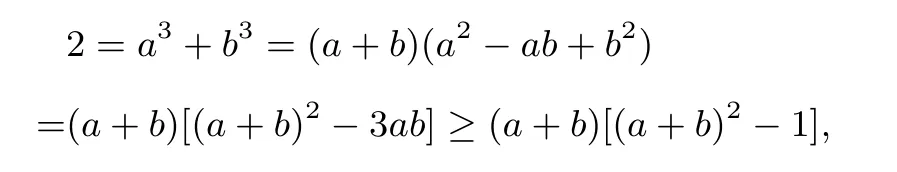
所以(a+b)3−(a+b)−2≤0,(a+b−2)(a+b+1)2≤0,

所以a+b≤2.

证法4(构建不等,一气呵成)因为

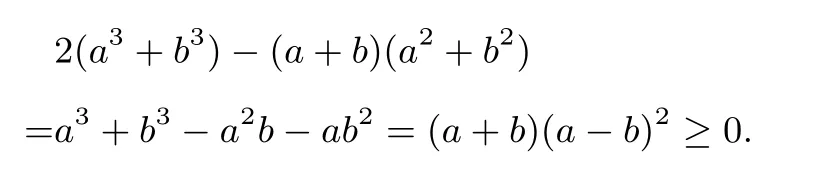
所以2(a3+b3)≥(a+b)(a2+b2).所以即(a+b)3≤8,故a+b≤2.

4.2 用分析法证明

证法 5(执果索因,逆流而上)要证a+b≤2,由于a＞0,b＞0,所以只需证(a+b)3≤8,展开得a3+b3+3a2b+3ab2≤8,只需证a2b+ab2≤2=a3+b3,即a2(a−b)+b2(b−a)≥0,因此只需证(a+b)(a−b)2≥0.这个不等式显然成立,故原不等式成立.

4.3 用比较法证明

证法6(作差比较,因式分解)

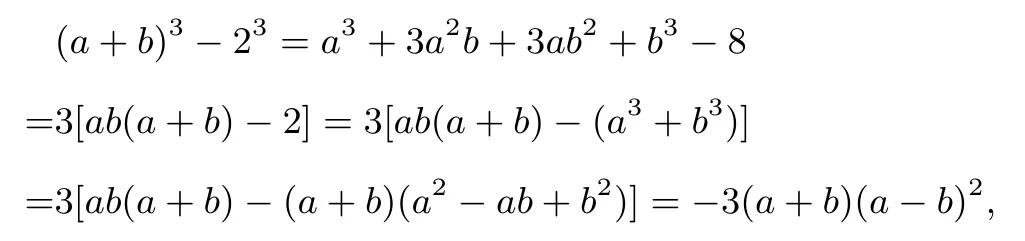
所以(a+b)3≤23,故a+b＜2.

4.4 用构造法证明

证法7 (相等入手,构造三元均值不等式)由结论可知,当a=b=1时等号成立,又a＞0,b＞0,得

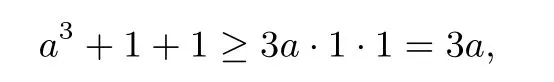
同理b3+1+1≥3b.两个不等式相加得,a3+b3+4≥3(a+b),所以a+b＜2.

证法8(构造等差数列,增设大小)由a3+b3=2知,a3,1,b3成等差数列,不妨设a≤b,所以,公差d=1−a3=b3−1≥0.所以(1−a)(1+a+a2)=(b−1)(b2+b+1).因为0＜a≤b,所以1+a+a2≤1+b+b2,所以1−a≥b−1即a+b≤2.

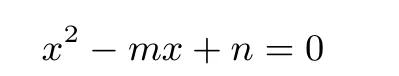
证法9(构造一元二次方程,用判别式)设a,b是方程的两个根,则a+b=m＞0,ab=n＞0.由a3+b3=(a+b)[(a+b)2−3ab]得m(m2−3n)=2,所以由∆=m2−4n≥0,得从而m3≤8,即m≤2,故a+b≤2.

评注 由m＞0可得m3−2＞0,即亦即综上可得

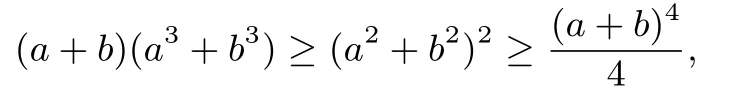
所以(a+b)3≤8从而a+b≤2.

评注 柯西不等式与向量法实质是一样的.

证法 11(确定主元,构造函数)设x=a,则b=

证法12(构造函数,利用凸性)构造函数f(x)=x3,显然f(x)在区间(0,+∞)上是一个下凸函数,所以对a＞0,b＞0,有

证法 13(构造函数,利用零点)令x=a+b,由a3+b3=2,得a3+(x−a)3=2,即x3−3ax2+3a2x−2=0.令

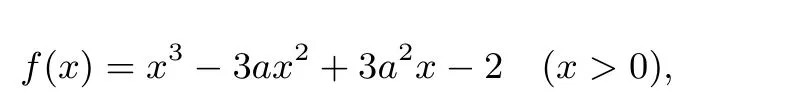
则f′(x)=3x2−6ax+3a2=3(x−a)2≥0,所以f(x)在区间 (0,+∞)上单调递增.f(0)=−2＜0,f(2)=6a2−12a+6=6(a−1)2≥0,所以f(x)在区间(0,2]上有唯一零点x0,即x0＜2.故a+b≤2.

4.5 用换元法证明

证法14(三角换元,焕然一新)设a+b=m＞0,故可设

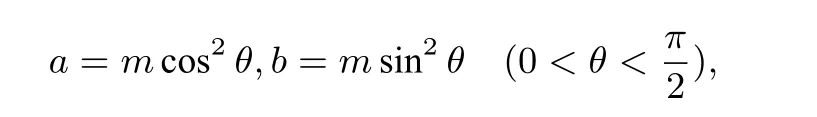
所以

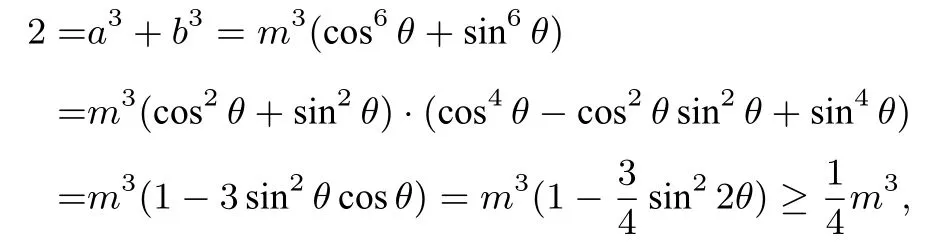
所以m3≤8,m≤2.又由上显然有2＜m3,即m＞故

证法 15(均值换元,利用导数)由a＞0,b＞0,a3+b3=2.不妨设a≤b,可设a3=1−x,b3=1+x,则其中0≤x＜1.令

4.6 用反证法证明

证法16(反设结论,导出矛盾)假设a+b≤2不成立,则有

因为6(b−1)2+2≥2,所以a3+b3＞2,这与已知条件a3+b3=2矛盾,所以原不等式成立.

评注 湘教版高中数学选修4-5《不等式选讲》第22页例1:设a3+b3=2,求证:a+b=2.证法16就是教材中例题的证明,并由此可知,没有条件a＞0,b＞0这道高考题的第(II)问也成立,也正因为增加了这一条件,证明才更加丰富多彩.可谓源于教材,高于教材.

关于第(II)问的证明,还有不少的综合法、构造法、函数法、换元法、数形结合法、反证法等,限于篇幅,从略.

5.第(II)问的变式探究

变式1 (弱化条件)若a,b∈R,a3+b3=2,求证:a+b≤2.

变式2(改变结论)若a＞0,b＞0,a3+b3=2,求证:ab≤1.

变式3(改变条件)若a＞0,b＞0,a2+b2=2,求证:a+b≤2,ab≤1.

变式4 (推广)若a＞0,b＞0,n≥2,n∈N,an+bn=2,求证:a+b≤2,ab≤1.

变式5 (改变条件和结论)若a＞0,b＞0,a+b=2,n≥2,n∈N,求证:an+bn≥2

变式6 (推广)若a,b,c∈R+,a+b+c=3,求证:a3+b3+c3≥3.

变式7(推广)若a,b,c∈R+,a3+b3+c3=3,求证:a+b+c≤3,ab+bc+ca≤3,abc≤1.

变式8 (再推广)若a,b,c∈R+,n≥2,n∈N,an+bn+cn=3,求证:a+b+c≤3,ab+bc+ca≤3,abc≤1.

证明 构造函数f(x)=xn(n≥2,n∈N),显然f(x)在区间(0,+∞)上是一个下凸函数,所以对a,b,c∈R+有

即

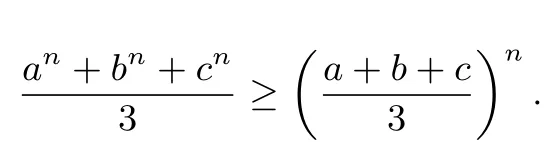
由an+bn+cn=3,可得a+b+c≤3.由(a+b+c)2≥3(ab+bc+ca)及a+b+c≤3,可得ab+bc+ca≤3.再由

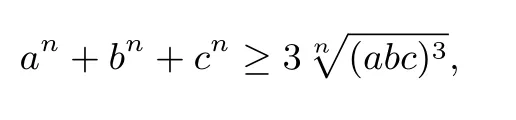
可得abc≤1.

变式1-7的证明不难,在此从略.

6.一点思考

高考主要考查通性通法,平常解题教学的重头戏也是通性通法的教学,但若长久如此,则会约束甚至扼杀学生的创新思维,而探究和创新正是新课改所追求的.因此,在解题教学中,教师首先要让学生独立思考、尝试解答,然后通过展示和交流,在不同的解法中指导学生分析哪些是通法,哪些是只适合本题条件的特技,当条件或结论改变时,教法是否也会改变,要让学生能够针对“题情”探索出适合自己的解题思路和方法.因此,在指导学生分析试题时,要充分挖掘试题的信息,充分联系所学的知识,改善习惯思维,训练思维的广阔性、灵活性、深刻性,升华解决问题的思想方法,培养学生的创新意识,提升学生的创新能力.