优化初三数学复习课教学的实践与思考

●童桂恒 (金华市第四中学，浙江 金华 321000)

优化初三数学复习课教学的实践与思考

●童桂恒
(金华市第四中学，浙江 金华 321000)

数学复习课是数学教学中一类基本的也是十分重要的课型.一堂高效的复习课不仅有利于学生掌握基础知识、基本技能、基本思想和基本活动经验，而且有利于提高学生的数学素养.反思当前数学复习教学中存在的一些低效乃至无效的教学行为，复习课要从“选、讲、练”这3个维度去平衡把握，通过“精选问题、分层施教、变式拓展”等方法，真正实现减负增效之目的.

复习教学；变式教学；分层教学；教学反思

数学复习课是数学教学中一类基本的也是十分重要的课型，要从“选、讲、练”这3个维度去平衡把握，要关注数学思维方法的训练，掌握数学的解题方法，同时也要注意纠正两种倾向：一是要避免“重思路引导，轻有效的巩固训练”；二是要避免“重策略探讨，轻必要的纠错过关”．一节课的内容不要贪多，复习时既要重视每年必考的重点内容和相关典型问题，强化主干知识的训练[1]，又要把握好重点内容与双基内容的复习时间与力度，反复训练，力求全面掌握，教后还要有跟进的题目加以巩固.

1 精选例题，方法变式

一道典型的例题，不仅具有巩固所学知识的作用，更有优化思维品质的功能.因此，在教学中教师要引导学生开展方法变式，在掌握通性通法的基础上，深刻分析命题条件的特殊性，让学生在问题的解决过程中对命题条件有本质的认识，从而达到会解一类题目的目的．

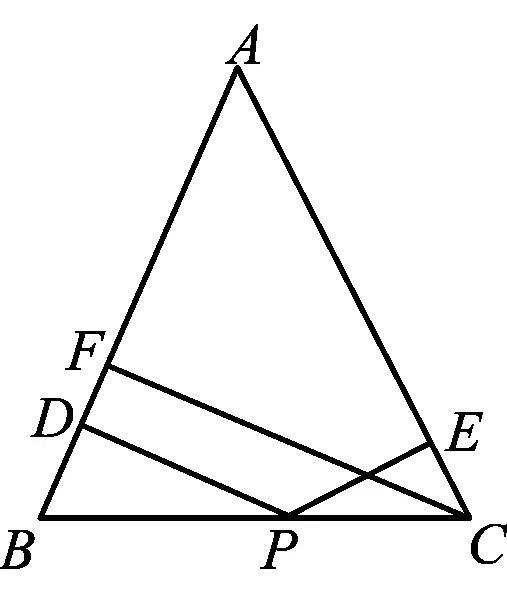
图1

例1[2]如图1所示，在△ABC中，AB=AC，P为BC上的一动点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E,CF为AB边上的高线．求证：PD+PE=CF.

分析 该例是平面几何中的一个典型问题，一般采用常规解法，即截长补短法．但是，通过详细分析发现，题设条件中包含着等腰三角形以及垂线段等特殊条件，因此，我们不禁要问：通过这些条件能否使证法更加简单呢？

证法1[2](截长法)如图2所示，过点P作PH⊥FC于点H，易证四边形DPHF为矩形.因此，PD=FH.

同理，易证Rt△PEC≌Rt△CHP，从而PE=CH，进一步得

PD+PE=FH+CH=CF.

图2 图3

证法2[2](截长法)如图3所示，过点D作DK∥BC交CF于点K，则四边形DPCK是平行四边形.由平行四边形的性质知，PD=CK，DK=PC.因为DK∥BC，所以

∠FDK=∠B=∠PCE.

又因为∠DFK=∠CEP=90°,所以

Rt△DFK≌Rt△CEP,

因此，FK=PE，进一步有

PD+PE=CK+FK=CF.

证法3 (补短法)如图4所示，过点C作CG⊥DP，交DP的延长线于点G,则四边形DGCF是矩形，从而FC=DG=PD+PG.进一步有∠PCG=∠B=∠ACP,因此，Rt△PGC≌Rt△PEC,从而PG=PE，于是FC=PD+PE.

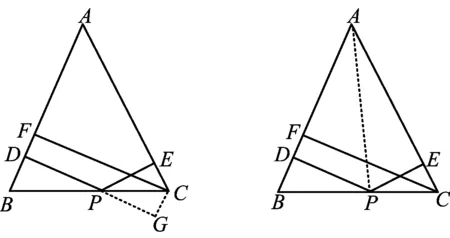
图4 图5

证法4 (面积割补法)如图5所示，联结AP.因为

而且S△PAB+S△PAC=S△ABC,所以

又因为AB=AC，所以PD+PE=CF.

证法5 (三角函数法)如图1所示，因为△PBD，△PCE和△BCF均为直角三角形，所以

PD=PBsinB，PE=PCsinC，FC=BCsinB.

又因为AB=AC，所以∠B=∠C，sinB=sinC，因此

PD+PE=PBsinB+PCsinC=

(PB+PC)sinB=

BCsinB=FC.

证法6[2](比例化归法)如图1所示，容易证明Rt△PBD∽Rt△CBF,从而

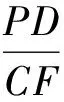
(1)

因为AB=AC，所以∠B=∠ACB，从而Rt△PCE≌Rt△CBF,因此

(2)

式(1)+式(2),得

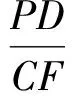
因此

PD+PE=CF.

反思 证法1～3采用的是通法，即求证“一条线段等于另外两条线段的和”问题，是解决该问题的基本策略[2]；证法4～6则通过挖掘其特殊性，在解题过程中有机渗透数学的转化思想.例如：由高线想到“面积割补法”(证法4)；由等腰三角形的特殊性质——两底角相等想到“三角函数法”(证法5)；由3个相似三角形想到比例化归法(证法6).在方法的变式中，学生的思维得到了发散，在证法的反思中，学生的能力分层得到了体现，教学的效果自然就得到了优化.

2 横联纵拓，题目变式

在初三复习教学中，根据问题的特点，设置题目变式，横向通过类比联想，纵向通过拓展延伸，“充分挖掘知识之间的联系，激活学生头脑中原有的相关知识和经验”[3]，从而建构起新的知识、方法网络．

图6

例2[4]如图6所示，在△ABC中，分别作它的内角平分线CE和外角平分线CF，求∠ECF的度数.

这是浙教版课标教材七年级下册第1.2节“三角形的角平分线和中线”第11页作业题第4题.当学生完成此题的解答后，教师可以通过横联纵拓、问题分层，使不同水平的学生在数学学习上得到不同的发展.也可以通过横向类比联想，让学生带着问题去思考、画出图形，并引导学生归纳、总结，最后得到3种不同类型的图形(如图7～9)，它们所体现的数学问题分别是[4]：

问题1 三角形不在同一顶点处的内角平分线和外角平分线的夹角问题(如图7).

问题2 三角形两条内角平分线的夹角问题(如图8).

问题3 三角形两条外角平分线的夹角问题(如图9).

图7 图8 图9

对于上述3个问题，教师可根据图形继续提出问题：“在图7～9中的∠CPB与∠A之间，分别有着怎样的关系？”学生的思维再次被激发.

通过对问题1～3的变式训练，可以有效地培养学生的数学发散思维能力，以及他们的创新意识.如果以上述问题为背景，在原图形的基础上对问题结论的规律作进一步的探究(即纵向拓展延伸)，那么学生不仅会一题，而且会一类，从而培养学生知识迁移的能力和应用知识解决问题的能力.

问题4 如图10，在△ABC中，∠A=α，∠ABC的平分线与∠ACD的平分线交于点A1;∠A1BC的平分线与∠A1CD的平分线交于点A2;…;∠A2 010BC的平分线与∠A2 010CD的平分线交于点A2 011，则∠A2 011为______.

图10 图11

问题5 如图11，在△ABC中，A1B,A1C分别平分∠ABC和∠ACB，A2B,A2C分别平分∠A1BC和∠A1CB,…,A2 011B,A2 011C分别平分∠A2 010BC和∠A2 010CB,则∠A3和∠A有何关系？你能探究出∠A2 011和∠A的关系吗？继续下去，若AnB,AnC分别平分∠An-1BC和∠An-1CB，你能用∠A表示出∠An吗？

图12

问题6 如图12，在△ABC中，A1B,A1C分别平分△ABC的外角∠DBC和∠ECB，A2B,A2C分别平分∠A1BC和∠A1CB,…,A2 011B,A2 011C分别平分∠A2 010BC和∠A2 010CB,则∠A3和∠A有何关系？你能探究出∠A2 011和∠A的关系吗？继续下去，若AnB,AnC分别平分∠An-1BC和∠An-1CB，你能用∠A表示出∠An吗？

3 精讲精练，过程变式

过程性变式是指在数学活动过程中，通过有层次的推进，使学生在分步解决问题中，积累多种活动经验、发展学生智力、提高运用知识能力的教学活动.复习课要做到精讲精练是不容易的,“精讲”不能理解为“少讲”，而是该讲的重点、难点,关键点要讲深、讲透；“精练”也不等于“少练”，而是该练的精编或精选题要练足、练全．

1)求点A,B,C的坐标；

2)求证：△ABC是直角三角形；

3)若坐标平面内的点M，使得以点M和点A,B,C为顶点的四边形是平行四边形，求点M的坐标(直接写出点的坐标，不必写求解过程)．

这是一道集代数(二次函数、二次方程)、几何(直角三角形、平行四边形)等重点知识于一体的中考试题.如何在讲授完该题之后，进一步拉长“知识链”，提出适合于不同层次学生需求的问题，让他们在解决问题的过程中积累解题经验，这需要教师课前进行精心预设．

通过变式1可以清楚地认识到：有些图形的对称性问题不一定需要通过图形去求解，而是可以通过挖掘出题目中隐含的规律，运用新的解题方法来解决．线由点组成，线的对称可以转化为点的对称，因此，关于x轴对称，即将y用-y替换，x不变；关于y轴对称，即将x用-x替换，y不变；关于原点对称，即将x用-x替换，将y用-y替换即可[5].

变式2 求△ABC的外接圆半径和内切圆半径．

变式3 点G为直角坐标平面内的一点，若以点A,B,C,G为顶点的四边形是矩形，求点G的坐标．

变式2和变式3是基础题，初三课堂教学要有一种保底意识，通过问题的分层，使一些暂时基础较差的学生也学有所获，而对基础较好的学生来说也能进一步打好知识基础.

变式4 在△ABC内部能否截出面积最大的矩形DEFG(顶点D,E,F,G在△ABC各边上)？若能，求出在边AB上的矩形顶点的坐标；若不能，请说明理由．

变式5 将△AOC沿y轴对折后，再绕点C按逆时针方向旋转90°得到△CFE(点A与点E对应)，判断点E是否在抛物线上，并说明理由．

变式6 设过点E的直线交边AB于点P，交边BC于点Q，使直线PQ分△ABC的面积为1∶3两部分？若存在，求出点P的坐标；若不存在，请说明理由．

变式7 在已知抛物线的对称轴上找一点P，使得△APC的周长最小，求点P的坐标及△APC的最小周长．

评注 课堂教学要抓中间促两头，变式4～7为中档题，这是复习教学中要下力气重点抓好的一档题，使一些暂时基础较差的学生“跳一跳也能摘得到”，而对基础较好的学生来说，这也是需要认真去做的问题.

变式8 若一个动点M自点P(0，1)出发，先到达对称轴上某点(设为点F),最后运动到点C.试确定使点M运动的总路径最短的点E和点F的位置，并求出这个最短路程的长[6]．

变式9 若一个动点M自点P(0，1)出发，先到达x轴上的某点(设为点E)，再到达抛物线的对称轴上某点(设为点F),最后运动到点C.试确定使点M运动的总路径最短的点E和点F的位置，并求出这个最短路程的长[6]．

变式10 若点Q是抛物线对称轴上的一个动点，点R是抛物线上的一个动点，使得以A,B,Q,R为顶点的四边形为平行四边形，求点R的坐标．

变式11 联结BC，点D是直线BC上方的抛物线上的一个动点，问：当点D运动到什么位置时，△BCD的面积最大？求此时点D的坐标和△BCD的最大面积．变式12 若平行于x轴的直线与该抛物线交于点H，K，且以HK为直径的圆与x轴相切，求此时圆的半径．

评注 变式8～12为稍难题，涉及最值问题、动点问题、分类讨论问题、转化思想、方程思想等，都是初中数学中最为重要的数学问题、数学思想.课堂要有灵动，需要对各层次学生的尊重，教学中既要有“保底”意识，也要有“探究”的勇气.教师要善于对已有的问题进行加工、变式、改造、整合，不断利用已有经验对问题进行变通推广、探索引申、提炼升华，以激发学生学习数学的兴趣，提升学生的创新思维能力.

总之，“数学复习课教学的优化”是一个永恒的话题，课堂的有效、高效是我们坚持不懈的追求.在复习课教学中，教师要以教材中的经典问题、生活中的数学问题、新颖别致的中考试题为切入点，充分挖掘典型问题的教学价值，通过变式教学、分层教学，使不同层次的学生在原有基础上都有所提高，使“不同的人在数学上得到不同的发展”的理念得到体现.虽然在目前班级授课制下，要真正做到教学面向全体学生实施分层教学、合理有效地进行变式教学难度较大，但仍值得我们继续去研究和探索．

[1] 林丹群,庄静云,陈清华.2011年“华约”自主招生笔试试卷评析暨2012年备考建议[J].福建中学数学,2011(11):6-11.

[2] 董玉峰.深化教学改革,构建高效课堂[ED/OL].https://wenku.baidu.com/view/562bd566caaedd3383c4d3b7.html,2012-11-27.

[3] 张国富.精制精导,点燃学生心智——浅谈一道源于课本的考题及其变式[J].青少年日记:教育教学研究,2013(7):40.

[4] 龙普云.从几道中考题说开[ED/OL].http://www.docin.com,2012-11-13.

[5] 邢成云.题组引领 梯度推进——例谈题组梯度复习法[J].中国数学教育,2010(Z2):34-37.

[6] 黄小芹.“线段之和最短问题”初探[J].中学数学,2012(8):66-67.

1 直觉性思维——反思的萌芽

图1

一般利用重心在向量中的表示形式来解决.

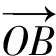
S△AOE=S△AOD=S△DOE.

易知S△AOD=2S△AOB,S△AOE=3S△AOC,S△DOE=6S△BOC,于是

就题目而言，我们已经解决，但如果能再仔细观察一下，发现答案3∶2∶1和题干中3个向量的系数比是一样的，这是巧合还是一般性结论，直觉告诉我们不能仅仅满足于答案，而应对此作进一步的反思和研究.

2 直觉到一般——反思的产生

通过直觉，笔者猜想如下的定理：

图2

证明 延长AO交BC边于点D.因为

所以

于是

上面证明了点O在△ABC内的情况，进一步反思：如果点O在△ABC外，是否还有同样的结论呢？仿照上面的推理过程，不难得到如下结论：

定理2 设O是△ABC外任意一点，△OBC,△OAC,△OAB的面积分别为S1,S2,S3.

1)当点O与点A在BC的异侧时，若S△OBC∶S△OAC∶S△OAB=λ∶u∶v,则

2)当点O与点B在AC的异侧时，若S△OBC∶S△OAC∶S△OAB=λ∶u∶v,则

3)当点O与点C在AB的异侧时，若S△OBC∶S△OAC∶S△OAB=λ∶u∶v,则

笔者从一个基本题目出发，通过反思发现了一般性的结论，在教学中反思能更有效地巩固基础，提高知识和方法的认识水平，通过有意识地反思，明确题目所覆盖的知识点，思考解决这类问题的一般方法.

3 一般性的延伸——反思的深化

此时，似乎已经完美地寻求到了问题的解决方案，爱思考的学生往往会对问题作进一步的反思.很多涉及到三角形的四心(重心、内心、外心、垂心)和向量结合的问题，能否利用上面的结论来建立一个统一形式？沿着这个思路继续思考问题，得到如下的定理：

1)若点O为△ABC的重心，则

λ1∶λ2∶λ3=1∶1∶1；

2)若点O为△ABC的外心，则

λ1∶λ2∶λ3=sin 2A∶sin 2B∶sin 2C；

3)若点O为△ABC的内心，则

λ1∶λ2∶λ3=a∶b∶c；

4)若点O为△ABC的垂心，则

λ1∶λ2∶λ3=tanA∶tanB∶tanC.

前面3个结论比较容易得到，下面对第4)个结论进行证明.

证明 如图3，因为H是△ABC的垂心，所以

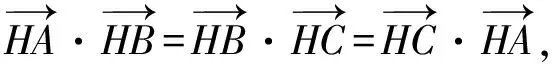
图3

又因为四边形AEHF的顶点A,E,H,F共圆，所以

∠A+∠BHC=π，

同理可得 ∠B+∠AHC=π，

故S△BHC∶S△CHA∶S△AHB=tanA∶tanB∶tanC.

利用化归的思想，通过一步一步反思，把这些看起来互不相关的问题都统一到一个形式上.罗增儒老师把解题后缺乏反思的现象比喻为“进宝山而空手返”.通过对已完成的思维过程进行周密且具有批判性地思考，进一步来探讨知识的内涵和外延，从中领悟数学思想方法，形成良好的认知结构，从而提高学生的元认知水平，完善知识体系.

4 成果应用——反思的再认识

通过以上的反思，学生的思维能力得到了提升，对问题的理解能力也更加深刻，下面我们把这些反思的成果应用到日常的解题中.

解 根据定理3，因为G为△ABC的重心，所以

56a=40b=35c，

即

代入余弦定理，得

故

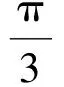
整理得

则

m∶n∶(1-m-n)=5∶5∶6,

解得

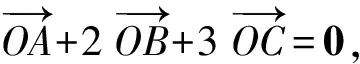
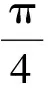
(2016年山东省高中数学联考试题第5题)

解 因为P为△ABC的外心,所以

根据已知条件，得

sin 2A=sin 2B，

又∠C=120°，从而

于是

故λ=-1.

笔者以一道常见数学题目为例，阐述了在数学教学过程中不断思考、不断反思问题以达到不断优化的目的.数学教学离不开解题教学，解题教学是数学教学的一个重要组成部分，在解题教学过程“如何引导学生思考、如何反思”是教师的一项重要工作.若平时在教学过程中能经常渗透这种意识，则学生会不断地实践并学会数学地思考问题，数学素养和数学品质也定能得到相应提升.

2017-06-30

童桂恒(1963-)，男，浙江开化人，浙江省特级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)09-01-04