引探究激兴趣，导探究挖潜能

福建省连城冠豸中学 杨伎芳

引探究激兴趣，导探究挖潜能

福建省连城冠豸中学 杨伎芳

没有思考就没有发现，没有发现就谈不上创造。而学数学就是启发人思考，引导人去探索，激发人去创造的活动。

与学生谈话发现，现在中学生学习数学都是比较被动，甚至是被老师牵着鼻子走的，平时他们智慧的体现主要是靠模仿、积累，很少有体现自我的“学和想”。作为教师，我们有责任抓住一切时机，特别是课堂的45分钟，引导学生自主学习、自主探究，让学生思维都动起来，还他们一个不一样的“我”！

一、在导入新知处引导探究

兴趣是最好的老师，学习一个新知识点，只要让学生感兴趣，那将会取到事半功倍的效果。而调动学习积极性贯穿课堂每一个环节，平时用得最多也最有效的常常是在导入新课这一环节。

例：在学习“求概率”这节课时，复习完上一节课知识后不直接引入如何求概率的方法，而是先引导探究：你觉得这个游戏公不公平？

游戏：A、B两个口袋中均有3个分别标有数字1、2、3相同的球，甲、乙两人进行摸球游戏。

规则：甲从A袋中随机摸一个球，乙从B袋中随机摸出一个球，当两个球上标的数字之和为奇数时甲赢，否则乙赢。

游戏一出，有的同学先猜测，有的同学直接想到前一节课上的概率知识进行探究，要看这个游戏公不公平，只要知道它们的概率就可以了。于是很多同学用推算的办法求出取出两个球的数字之和为奇数的概率为4/9，偶数的概率为5/9，所以这个游戏不公平。

这样一探究，学生的兴趣立刻被调动起来，原来数学知识这么有用，从而激发学生往下学习的欲望：有没有更快更好的办法求概率呢？进一步提高新知的学习效果。

二、在练习变式处引导探究

现在课本的例题和练习，可以说大部分是着重于基础知识和基本技能的训练与巩固，单纯练这些往往不能满足一部分潜能较大的学生，也不利于学生思维灵活性、创造性的发展。所以，在课本例题和练习基础上做些变式练习是很有必要的。

例：在学习“中心对称图形”时，有两道练习：①说出一些中心对称图形；②识别汽车标志中哪些是中心对称图形。这样练习完后，还不能很好地体现中心对称在生活中的广泛存在。为了体现旋转变换的数学魅力，我又设计了两道变式练习引导学生探究：

（1）任意一个自然数旋转180°后，可以发现一些有趣的现象，请你找出一个五位数，使其旋转180°后还是原来的五位数（各个数位上的数字不得完全相同）。

学生探究：自然数中0、l、8是中心对称图形，而6、9是关于某点中心对称，所以可以从0、l、8、6、9中选择组成五位数。

（2）用四块如图所示的正方形瓷砖拼成一个新的正方形，使拼成的图案是一个中心对称图形。

学生操作结果展示：

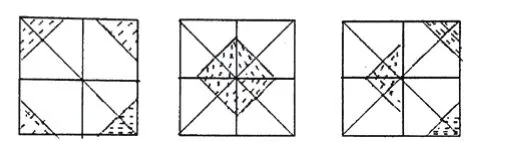
通过变式练习的探究，学生发现生活中处处存在中心对称美，特别是通过图形设计，使他们对中心对称有了更深的了解，从而培养学生观察、分析、想象、动手、操作的能力，也激发了他们的学习兴趣。

三、在总结归纳处引导探究

在总结归纳处引导探究往往能使知识得到一次强化，思想方法得到一次对比、提炼，从而更好地内化为个人的知识技能。

例：在“二次函数”的复习中，通过基本知识和一些简单练习后引导学生归纳总结：求二次函数解析式有几种方法？

学生总结：

①知道任意三个点坐标可用一般式：y=ax2+ bx+c；

②知道顶点坐标或对称轴可用顶点式：y＝a(x-h)2+k;

③知道与x轴的交点坐标，可用交点式：y=a(x-x1)(x-x2)。

学生总结后又引导学生回到前面做完的练习上：已知二次函数图象经过(3，0),(1，8)，(-1，0)三点，求其解析式。

师：刚才大家都用一般式或交点式解出来了，那么这题还能用顶点式吗？（学生前面都没有想过）

学生立即动起来，观察三点坐标，发现因二次函数的对称性可知(3，0),(-1，0)是对称点，所以对称轴是x=1，而又有点(1，8),所以(1，8)就是这个二次函数图象的顶点，所以这题也可用顶点式。

学生探究完后有种豁然开朗的感觉，原来题目中还隐藏了条件，还有这么简便的方法。通过这次探究，学生更懂得审题观察的重要性。一个题目拿到手，学会了不急于下手，而是先考虑方法；不会机械模仿例题，而是用探索方法体现智慧。

四、在拓展延伸处引导探究

在近几年的中考试题中，有关动点、旋转的考查学生操作、想象、探究能力的中考题层出不穷。作为教师，当然不能就题讲题，还要适当拓展延伸，引导学生更全面地探究，这样才能让学生举一反三，灵活多变，学会一题多变，一题多解。

例：一道中考题的探究：如图，直线AC∥BD，连接AB，直线AC、BD及线段AB把平面分成①②③④四个部分。规定：线上各点不属于任何部分，当动点P落在某个部分时，连接PA、PB，构成∠APB、∠PBD、∠PAC三个角。

①当动点P落在第①部分时，说明：∠APB=∠PAC+∠PBD。

②当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立？

③当动点P在第③部分时，全面探究∠PAC、∠APB、∠PBD之间的关系，并写出动点P的具体位置和相应结论。

题目一读完，教师引导思考：要解决角之间的关系，可依据哪些知识点入手呢？

经过一番思考讨论，学生回忆得出：一是平行线构成的角的关系，二是三角形构成的角的关系。这时，学生就找到了解决问题的切入点，过P作AC的平行线，从而用平行线性质解决角之间的关系。

解完后，在学生学习添加辅助线的方法和分类讨论思想后再次展开探究：当动点P在第④部分时，全面探究∠PAC、∠APB、∠PBD之间的关系，并写出点P的具体位置和相应结论。这时的探究解答学生应顺水推舟了，很快有了结果。这样的多次探究使学生对解题方法、分类讨论思想得到进一步加固。

总之，学数学就是让学生思考、学会分析，从而自主解决现实生活中的数学问题。我们应多巧妙设计一些问题练习，引导学生探究，从而培养他们的观察力、分析力、创新力，同时为今后的继续深造奠定基础。