重复补偿控制PID控制器的设计与仿真

王辛望，沈小林

(中北大学 计算机与控制工程学院，山西 太原 030051)



重复补偿控制PID控制器的设计与仿真

王辛望，沈小林

(中北大学 计算机与控制工程学院，山西 太原 030051)

针对非线性系统在工程中广泛应用的各种传统和新型PID控制方法的优缺点和实际应用中遇到的问题，提出了传统PID控制和一种新型重复控制补偿的PID控制。利用Matlab进行仿真并根据两种控制算法的效果进行对比，根据确定性和随机性的指标对系统性能进行了分析。依据实验得出的结果，对两种不同的PID控制进行了评价。

PID；Ziegler-Nichols；重复控制；Matlab

据统计，在工业控制应用中多数控制系统都具有PID结构，而PID控制方法的大量使用，根本原因在于PID控制具有以下优点：原理简单、使用简便，PID的参数Kp、Ti、Td可以通过过程动态特性及时调整，具有适应性和鲁棒性强等优点。但是，面对多种多样的PID控制方法，在实际应用中如何选择已成为工程人员难题[1]。

结合以往控制工程的整定方法，介绍了Ziegler-Nichols法。但是随着先进PID理论的兴起和工程复杂程度的逐步增加，早期的方法已无法适应越来越复杂的工程应用，所以又提出了基于重复控制补偿的PID控制器。通过Matlab提供的强大平台进行仿真[2]，主要从跟踪性、抗干扰性和鲁棒性3方面进行对比研究。

1 算法

PID控制器就是依据设定值与实际值之间的误差，通过运用比例(P)、积分(I)、微分(D)等基本控制规律，亦或将它们根据实际工程应用的需要，形成有PI、PD和PID等复合控制规律，使控制系统达到性能指标的要求。

在PID中3个参数Kp、Ti、Td的作用能够直接影响到控制效果的优劣，所以想要获得最佳控制效果，必须修改比例、积分和微分3种控制的作用。总的来说，比例控制主要是针对偏差的“粗调”，确保控制系统的“稳”；积分控制主要是针对偏差的“细调”，确保控制系统的“准”；微分控制主要是针对偏差的“微调”，确保控制系统的“快”[3]。

在PID调节器的作用下，依次对误差信号比例(P)、积分(I)、微分(D)控制进行组合。调节器的输出看作被控对象的输入控制量。PID控制算法的模拟表达式为

(1)

相应的传递函数为

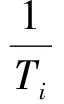
(2)

其中，Kp是比例系数；Td是微分时间常数；Ti是积分时间常数。

1.1 传统PID控制

传统PID控制(Ziegler-Nichols) 整定法需要建立一个能如实反应被控对象频域特性的模型，根据该模型，结合给定的性能指标可推导出公式，然后用于PID参数的整定。被控对象模型的确定的具体步骤是先通过实验，求得控制对象对单位阶跃输入信号的响应，若阶跃响应曲线呈S形，那么被控对象传递函数可近似为

(3)

利用其放大倍数K、时间常数T和延迟时间τ,依据表1中的公式可确定Kp、Ti和Td的值[4]。

表1 Ziegler-Nichols 整定法整定控制器参数

1.2 重复控制补偿的PID控制

1981年日本学者Inoue首先提出了重复控制，适用于伺服系统重复轨迹的高精度控制。重复控制能够提高系统跟踪精度，其原理来自与内膜原理[5]。

加到被控对象的输入信号除偏差信号外，还叠加了一个“过去的控制偏差”，该偏差是上一周期该时刻的控制偏差。将上一次运行时的偏差反映到现在，与“现在的偏差”一起加到被控对象进行控制，这种控制方式，偏差重复被使用，称为重复控制。经过几个周期的重复控制之后，能够显著提高系统的跟踪精度，改善系统的品质。这种控制方法不但能适用于跟踪周期性输入信号，而且还可以抑制周期性干扰[6]。

在重复控制中，一般期望重复控制作用在高频段的增益减小。因此，在重复控制中通常加入低通滤波器Q(s)。本控制方法取

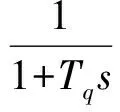
(4)

其中，Tq>0为滤波器的时间常数。

重复控制信号是周期性信号，其基本结构如图1所示。应用重复控制不仅可以提高系统的跟踪精度，还可以提高系统的鲁棒性。

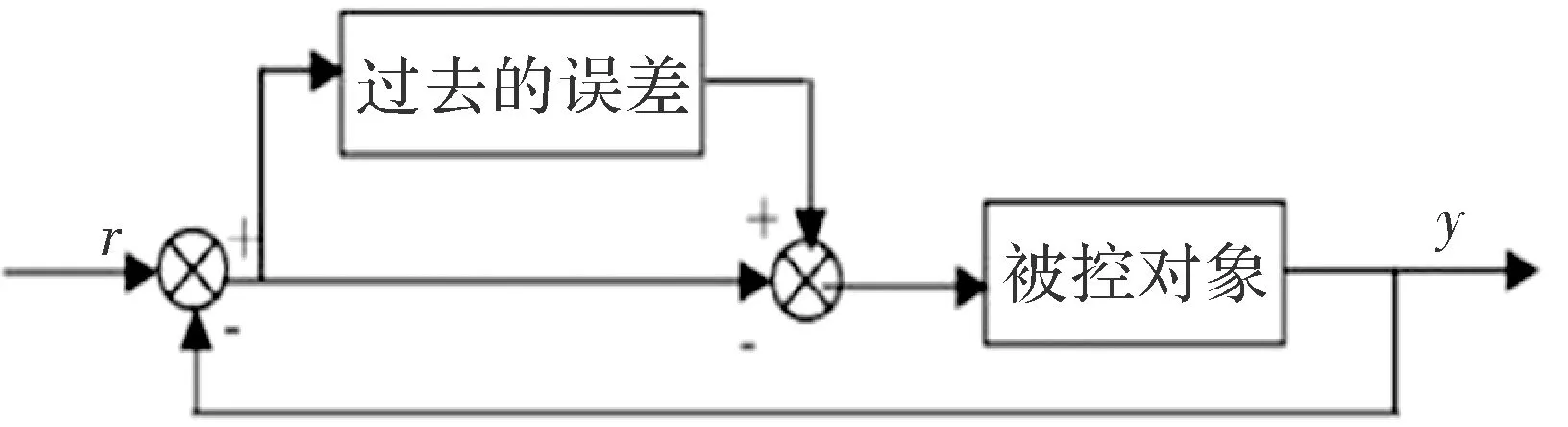
图1 重复控制原理图

基于重复控制补偿的PID控制系统框图如图2所示，其中up(k)为PID控制的输出；ue(k)为重复控制的输出；Q(s)为低通滤波器[7]。控制算法为

u(k)=up(k)+ue(k)

(5)

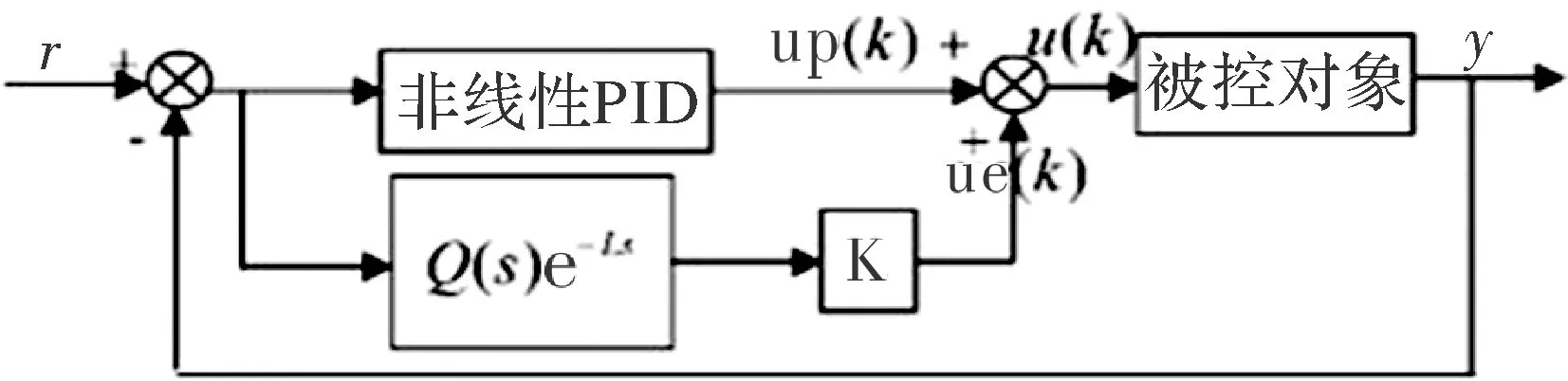
图2 重复控制PID结构框图

由图2可以分析出，传统的重复控制PID存在两点不足。首先，根据上述算法分析，重复控制并不是接到指令后马上开始运行，还要滞后一个周期才能输出，因此在第一个周期中，系统的误差、干扰等因素会影响系统的控制，并影响到系统的性能。其次，由于延迟环节的影响，系统在第一个周期内没有信号的输出[8]。

图3 新型重复控制PID的结构框图

为解决上述两点不足，改进重复控制补偿PID的精度，将重复控制补偿PID与传统PID相结合，组合成一种如图3所示的新型重复控制补偿PID的控制方式，重复控制器用以消除跟踪误差，PID控制器用以调整输出信号，使跟踪误差减小[9]。

2 仿真

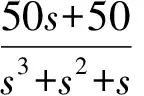
图4 Simulink仿真图

图5 普通PID输出跟踪曲线

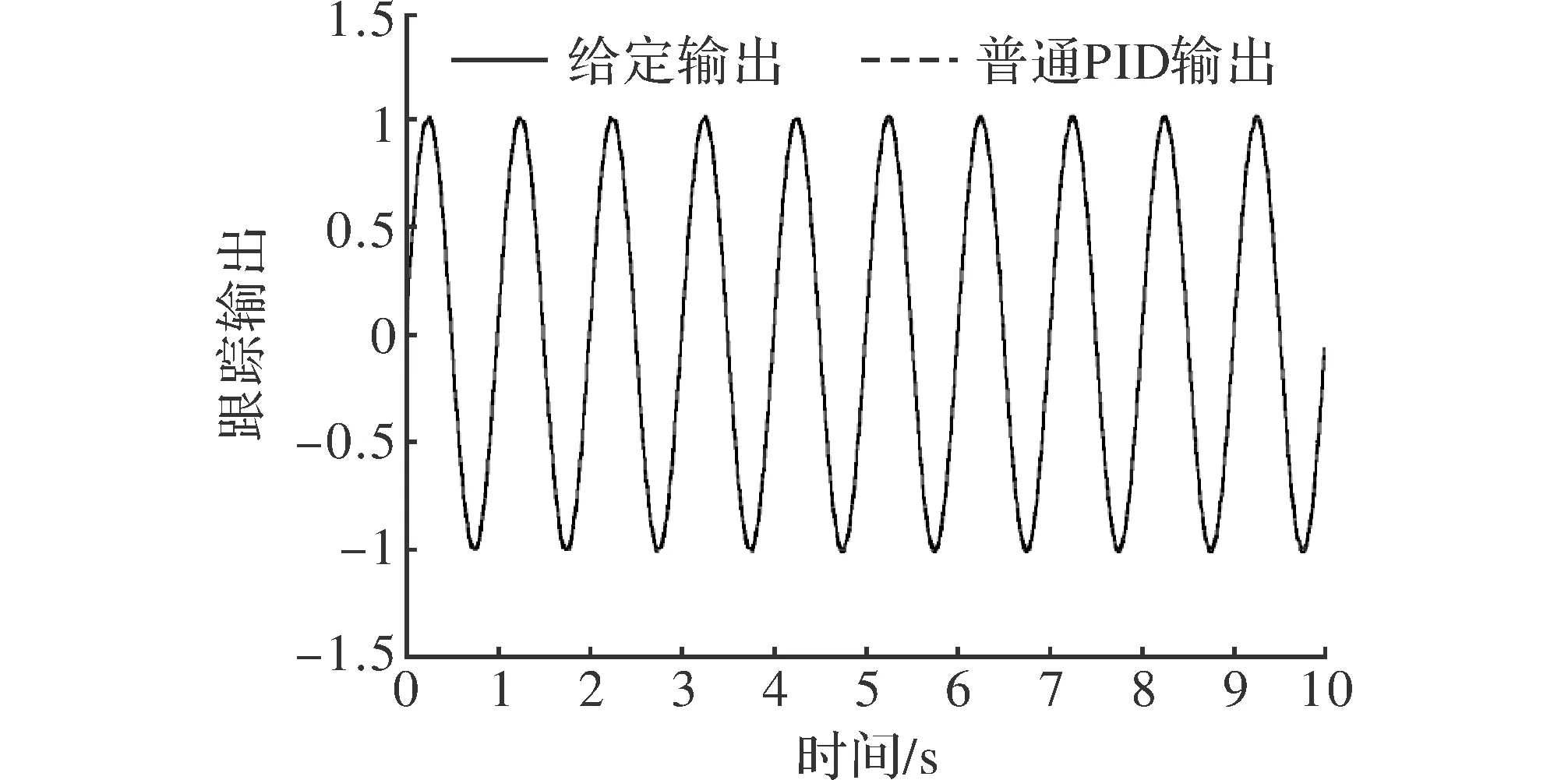
图6 重复PID输出跟踪曲线

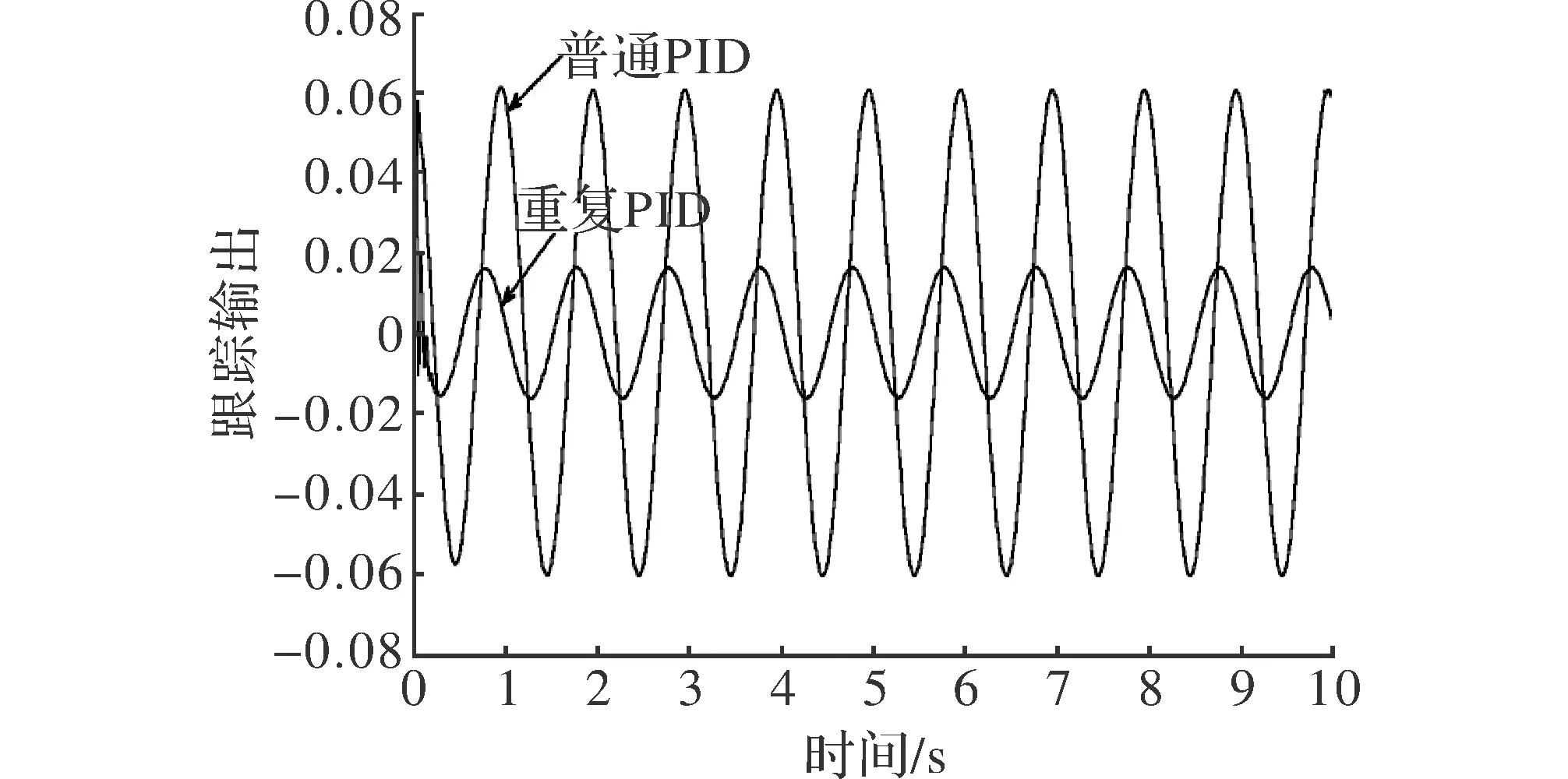
图7 普通PID与重复PID误差跟踪曲线

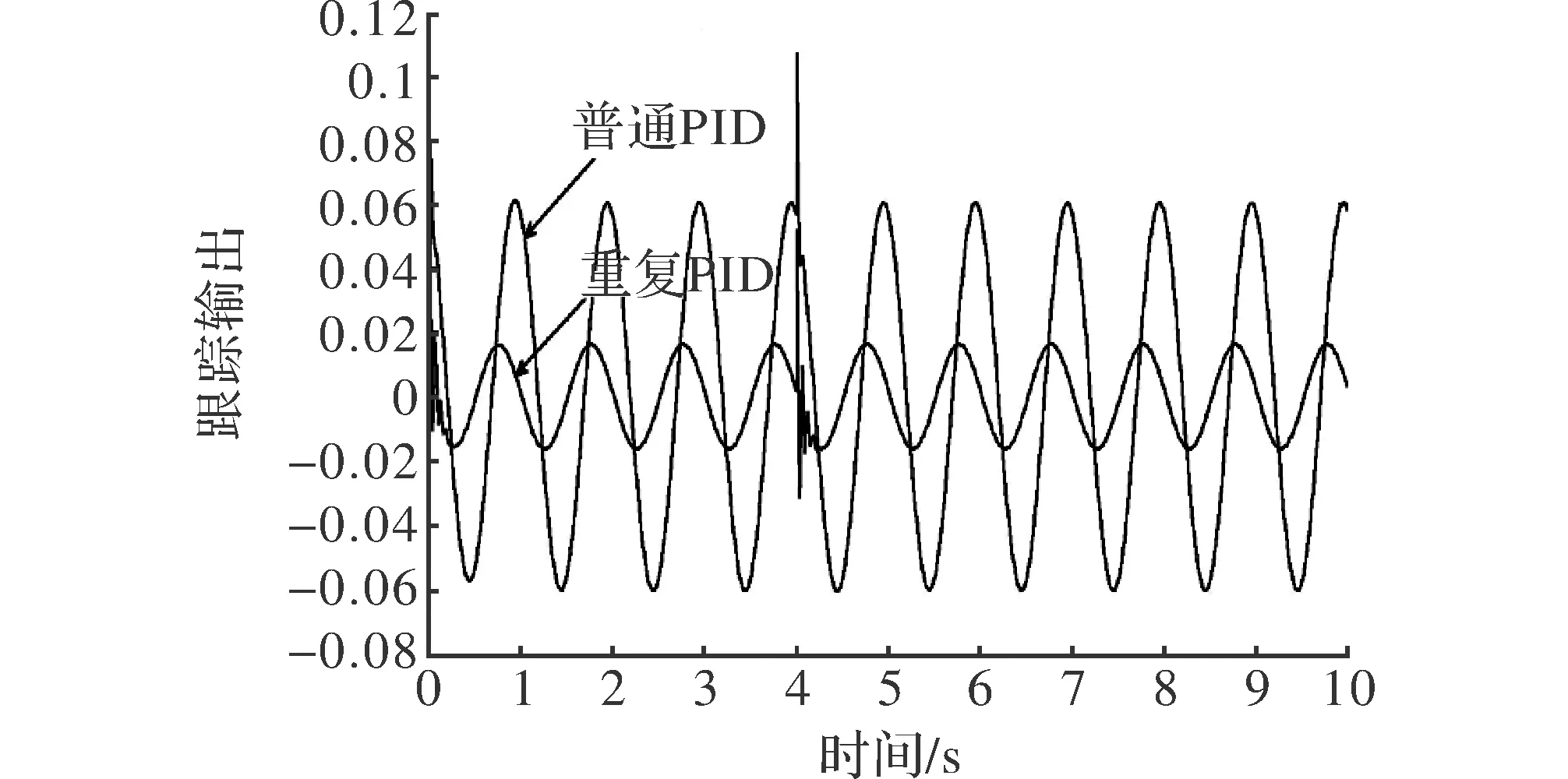
图8 普通PID与重复PID扰动误差跟踪曲线

经过仿真，普通PID控制器和基于重复补偿控制PID控制器的输出图像如图5和图6所示，PID控制器和基于重复补偿控制PID控制器的误差曲线如图7所示，干扰误差曲线如图8所示[11]。

根据仿真曲线可以看出，图5和图6都能基本跟踪所给出的正弦信号，但是图6基于重复补偿控制的跟踪更加精确；从图7的误差曲线可以看出，基于重复补偿控制PID比普通PID控制提高了控制的精准度；图8说明当有周期性干扰存在时，在新型重复补偿控制PID控制器的作用下，系统的跟踪精度显著提高，并且经过几个周期的变化，逐渐平稳，说明其具有良好的鲁棒性。

3 结束语

在传统PID控制的基础上，结合PID控制的缺点和新型PID控制的优点，提出了一种新型的重复补偿控制PID的控制方式。根据仿真结果可以看出，运用新方法可以提高控制精度、抗干扰性和鲁棒性[12]。对被控对象严重的非线性特性、强耦合性都具有良好改善作用[13]，并且对解决交流伺服系统的负载扰动问题有所帮助[14-15]。

[1] 王蕾,宋文忠.PID控制[J].自动化仪表,2004,25(4):1-6.

[2] 徐昕.Matlab工具箱应用指南：控制工程篇[M].北京:电子工业出版社,2000.

[3] 王伟,张晶涛.PID参数先进整定方法综述[J].自动化学报,2000,26(3):347-355.

[4] Åström K J,Hägglund T.Revisiting the Ziegler-Nichols step response method for PID control[J].Journal of Process Control,2004,14(6):635-650.

[5] 赵志诚,张博,刘志远,等.一种分数阶系统内模PID控制器设计方法[J].信息与控制,2014, 43(2):129-133.

[6] 刘金琨.先进PID控制及其Matlab仿真[M].北京:电子工业出版社,2003.

[7] 陶永华,尹怡欣,葛芦生.新型PID控制及应用[M].北京:机械工业出版社,2002.

[8] 詹习生,张先鹤.重复补偿PID控制在交流伺服系统中应用[J].电气传动,2009(10):55-58.

[9] 苏义鑫,蔡丹丹,王雁.基于重复补偿控制的交流伺服系统的PID控制[J].控制工程,2011,18(5):685-687.

[10] 范振瑞.基于Matlab的PID温度控制系统设计[J].电子科技,2013,26(8):164-167.

[11] 张丹红,胡孝芳,苏义鑫,等.结合重复控制补偿和CMAC的液压伺服系统PID控制研究[J].机械科学与技术,2012,31(5):749-752.

[12] 刘迪,李岩,张大为.一种改进型自适应PID控制算法的仿真与研究[J].仪表技术,2014(3):50-51.

[13] 蔡淑敏,王亚刚,田涛.智能PID控制算法研究及Matlab实现[J].电子科技,2016,29(7):43-47.

[14] 邵俊鹏,张领,金朝辉.基于重复控制补偿的电液位置伺服系统分数阶PID控制[J].北京工业大学学报,2015(4):519-525.

[15] 张立强,杨国来,龚海峰.基于重复控制补偿的电液位置伺服系统PID控制[J].机床与液压, 2005(8):112-112.

Design and Simulation of PID Controllers with Repetitive Compensation Control

WANG Xinwang, SHEN Xiaolin

(School of Computer and Control Engineering, North University of China, Taiyuan 030051, China)

This paper proposes a novel repetitive control compensation PID control based on the nonlinear system. MATLAB simulation is performed of the effect of two control algorithms, and an analysis is made of the performance of the system with deterministic and stochastic indicators. The two different PID control are evaluated based on the experimental results.

PID; Ziegler-Nichols; repetitive control; Matlab

2016- 08- 21

王辛望(1991-)，男，硕士研究生。研究方向：控制理论与控制工程，导航等。

10.16180/j.cnki.issn1007-7820.2017.07.010

TP273

A

1007-7820(2017)07-037-03