基于改进Floyd算法的城市交通网络最短路径规划

徐 达，蔡满春，陈 悦

(中国人民公安大学 网络安全保卫学院，北京100038)



基于改进Floyd算法的城市交通网络最短路径规划

徐 达，蔡满春，陈 悦

(中国人民公安大学 网络安全保卫学院，北京100038)

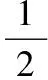
改进Floyd算法；最短路径；城市交通网络

城市交通道路高速发展使得交通网络间节点与路段日趋复杂，在城市交通网上规划最短路径也成为研究热点之一。最短路径规划不局限于路径规划，还可引申至时间、费用等其他度量，在城市最短路径规划算法选择上，使用最频繁算法为Floyd算法。刘海洋等[1]在研究分析公交车道设置的基础上，提出基于Floyd算法城市最短路径的规划，有效解决公交车道设置问题，但未将算法改进，从而导致在公交车道设置过程中出现计算量大、计算效率低的情况；张荣等[2]在分析了城市建筑较多导致交通道路趋于复杂和到达目的地线路过多导致出行路径不合理后，结合 Floyd 算法体系，提出最优路径、动态调整的思路，虽然有效解决城市交通节点最短路径规划问题，但也未将Floyd算法进行改进，从而使得整个城市交通节点规划最短路径过程中冗余计算量增大，效率降低。国内外学者对Floyd算法进行深入研究[3-9]，提出了改进思想。林华珍等[10]将Floyd算法进行优化，降低计算量，提高了算法计算效率；赵礼峰等[11]将Floyd算法改进，并通过添加下标更直观展示最短路径规划过程中选择的节点，进一步优化Floyd算法，大幅提高了计算效率。本文总结分析了现有研究成果，在城市交通道路节点最短路径规划过程中选择改进Floyd算法，减少Floyd算法计算过程的非必要计算，整体提高计算效率，完成城市交通网络中各个节点之间最短路径规划。

1 相关知识分析

1.1 城市交通网络特点分析

城市交通道路节点在整个交通网络中发挥着重要功能，在道路的机动性、通行能力、路网容量都具有较大影响，根据文献[12]可归结为数据量大和结构复杂，城市道路的复杂性给在城市交通网络节点与节点间最短路径选择造成一定困难。

根据实际需求对包括大量节点及路段的城市交通网络进行抽象，表现其复杂特性，建立合适模型对其进行分析，将改进Floyd算法应用到城市交通网络节点间路径规划，能够有效解决最短路径规划问题。

1.2 算法相关知识

赋权图：有向网络图D={v，w}，节点依次标号为vi(i=1,2,3,…,n)，在节点vi与vj之间的距离为wij=m，并将其标示在网络中。

回路：在有向网络图D={v，w}中含有一条起点和终点相同的路。

负回路：回路的一种，其权值总和在回路上是负值。

距离矩阵：把最短路径的长度记录在一个n阶矩阵D中，矩阵的第i行到第j列的元素dij指出了从第i个节点到第j个节点之间最短路径的长度。

最短路径：一般指距离长短，也可引申为花费时间、消耗代价等。

Floyd算法：Floyd算法与Warshall算法相类似，通过一系列n阶矩阵来计算一个n顶点加权图的距离矩阵，其核心思想表述为

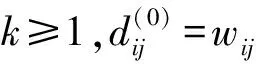
(1)

2 改进Floyd算法

2.1 改进算法思想

2.2 改进算法步骤

改进Floyd算法的主要步骤如下：

步骤1 根据有向网络图得出距离矩阵

(2)

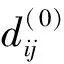
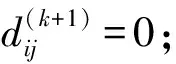
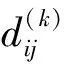
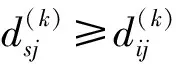
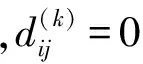
(3)

(3)i>j时

(4)

在此步骤中能将D(k)现有最短路径与基于D(k)基础新得出最短路径进行比较，从而选出两者之间的最小值作为D(k+1)的最短路径；

步骤6 若D(k+1)=D(k),则表明当前路径矩阵为最终结果，否则跳转至步骤2，进行新一轮计算。

2.3 改进Floyd算法分析

Floyd算法的基本定理保证了Floyd算法的可行性和正确性[15]。本文改进算法基于Floyd算法，思路与Floyd算法无太大差异，只在计算步骤上进行改进，可见改进算法是正确可行的。

3 建模与分析

3.1 建模实例

模拟城市交通网络节点之间最短路径规划，截取城市某个区域的交通网络结构图作为模型背景图案，如图1所示。

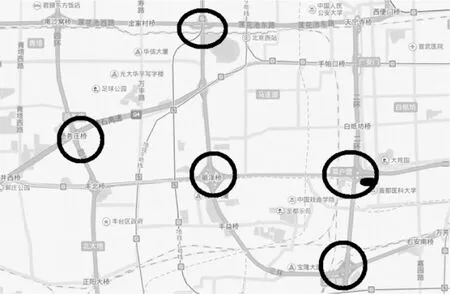
图1 城市交通网络图

对图1进行分析，构建合适的有向网络赋权图模拟城市道路交通网络，在图2的网络图中，通过改进Floyd算法对任意两个节点之间最短路径进行规划。

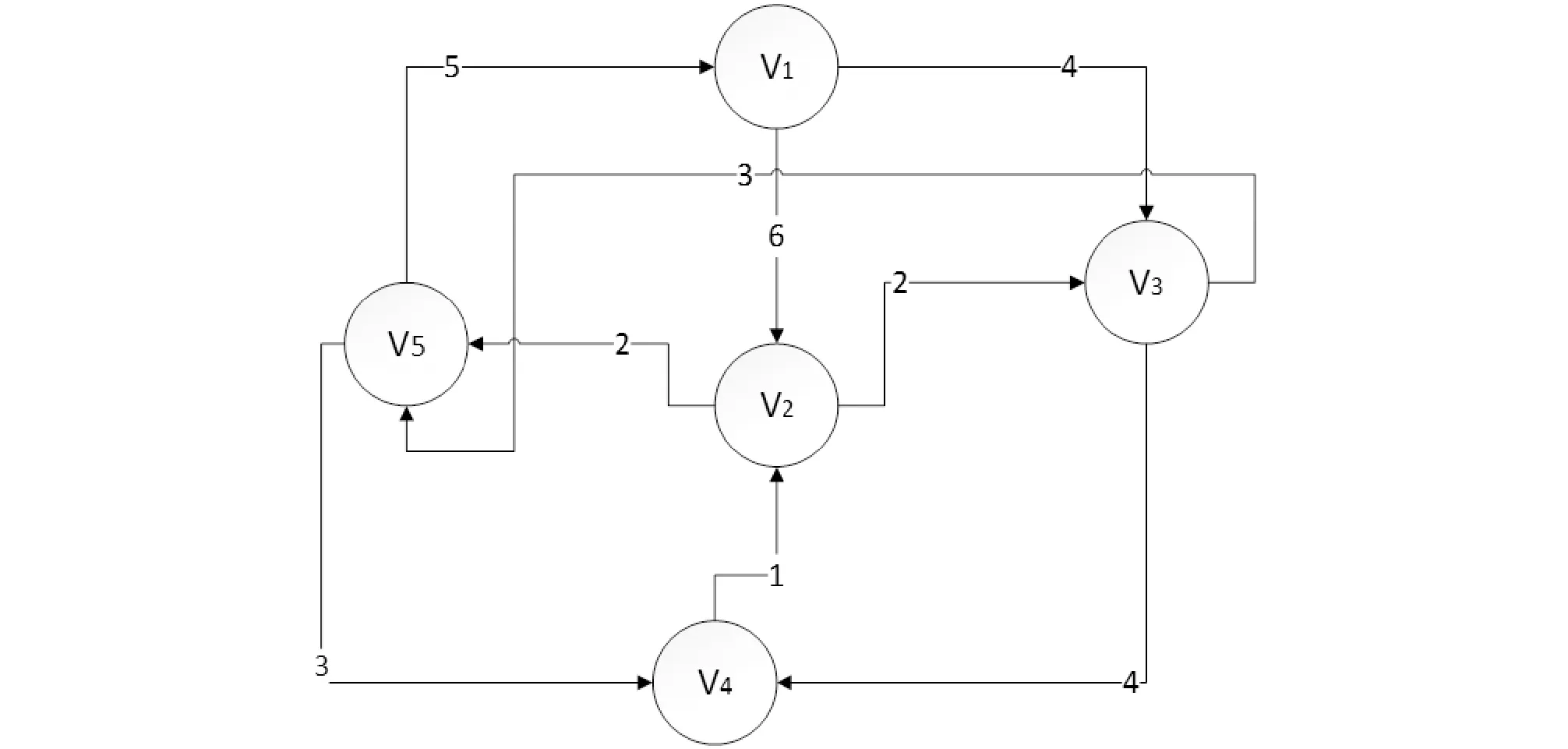
图2 有向网络赋权图

3.2 本文建模说明

说明1 本文在建模中保留城市道路交通的部分属性以及完整的拓扑结构，道路交叉抽象为网络节点，交叉口之间路径抽象为城市交通网络边；

说明2 文中有向网络赋权图节点代表从城市交通网络区域中选取的节点，未被选取的节点不纳入规划考虑范围之内；

说明3 城市道路交通网络中的通行道路在实际中均为双向路径，在本文中标注为单向；

说明4 城市道路交通网络中的权值标注在实际运用中需综合考虑节点之间路径实际长度和路况信息等，并结合专家建议进行标注，在本文只考虑节点之间路径长度；

3.3 实例演示

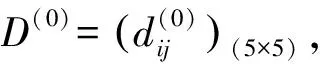
(5)

通过改进Floyd算法由D(0)计算D(1)之前，将有向网络图进行转换，得到如图3所示的双节点之间关系，更直观标识出需要参加计算的节点和不需要纳入计算的部分节点。

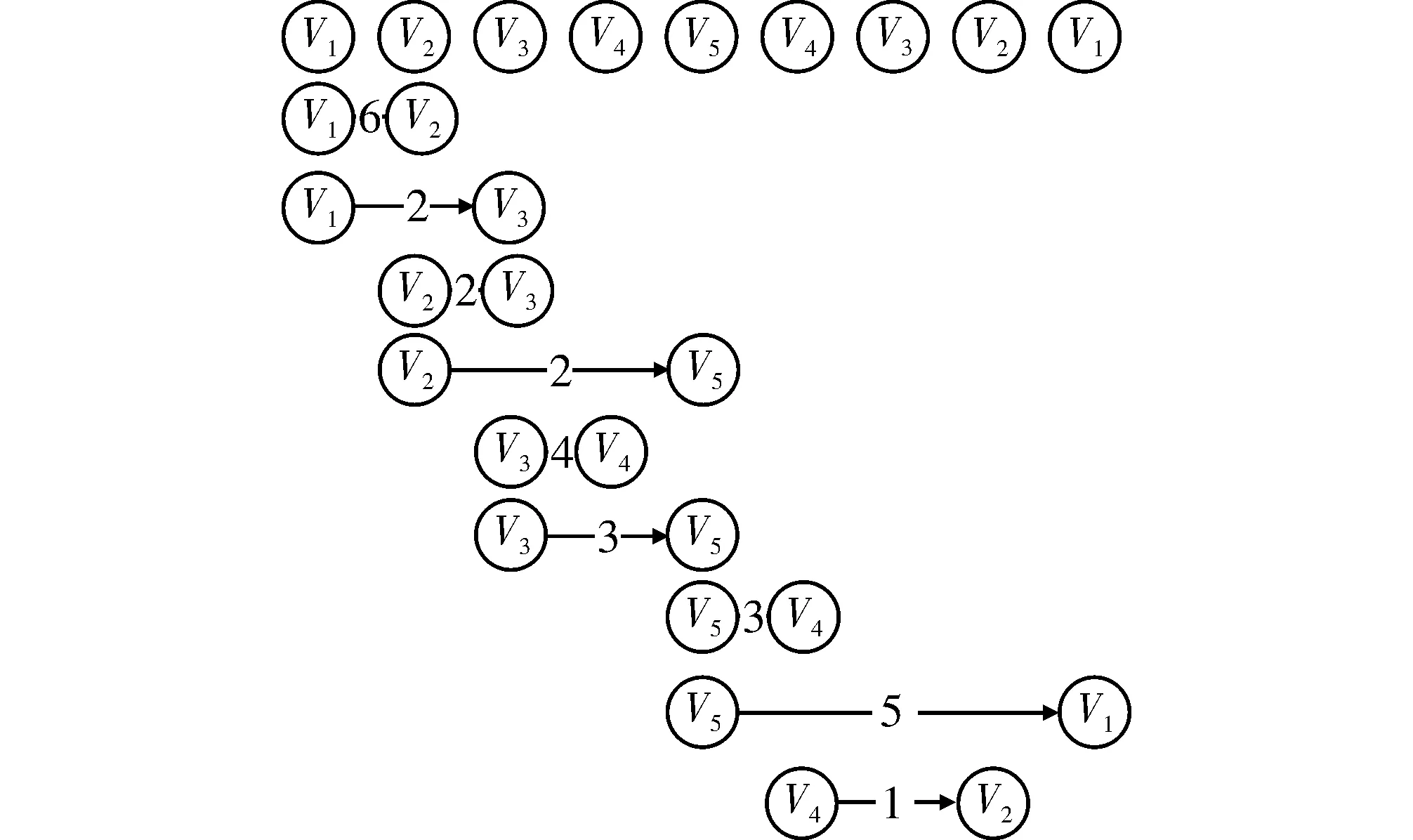
图3 有向网络图转换双节点权值图

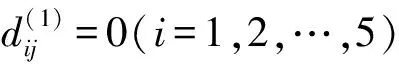
由D(0)来计算D(1)

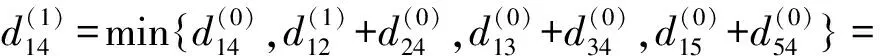
(6)

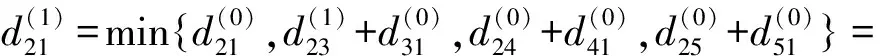
(7)

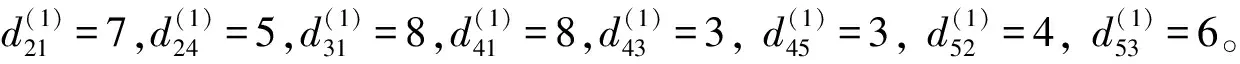
(8)

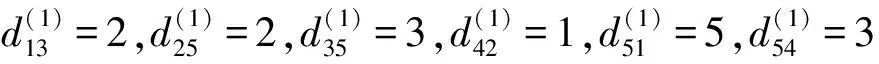
(9)

经比较D(2)=D(1)，则表明当前所得结论为有向网络最短路径规划最终值。

3.4 结果分析

3.4.1 算法的优越性

对于本文的算例，使用Floyd算法需要算法进行125次计算，用文献[16]中的优化矩阵计算需要进行75次计算，改进Floyd算法将非必要计算省略，只需要33次计算。Floyd算法在本算例中，由权值矩阵D(0)将vi到vj经过的所有路径计算出来，选择其中最短路径更新至D(1)中，经过如此数次迭代直至得出D(k)，计算较繁杂。总结分析发现改进Floyd算法，在节点vi和vj之间最短路径规划过程中，不相连的节点或通过某些中间节点vs相连的路径都将在判断是否应当舍弃后再进入计算，从而降低计算复杂度并完成城市道路交通节点间最短路径规划。

3.4.2 改进算法实用性

本文改进Floyd算法将降低计算复杂度，提高工作效率，改进Floyd算法能够较好的完成在城市交通网络节点间的最短路径规划任务。在城市最短路径规划过程中，各个节点之间的路径权值赋值，需要根据城市交通道路宽度、道路质量、阶段道路车速和路面状况等信息综合考虑。改进算法提高计算效率，在码头货物在多仓库之间的分配[17]、分布式电源孤岛划分[18]、带宽预分配、空中交通流量管理[19]、道路的优化[20]、交通抢修、事故救援和路径导航中都具有较大实用价值。

4 结束语

改进算法基于Floyd算法思想，在算法工作流程上进行改动，采用先比较再计算模式降低冗余计算量，提高计算效率，完成在城市交通道路节点之间最短路径规划。在城市交通网络中规划最短距离的路径规划过程中需要考虑的因素较多，为方便演示，本文路径权值未覆盖全各道路交通因素，下一步工作将综合多因素到城市交通中，体现基于改进Floyd算法城市交通网络最短路径规划方法处理复杂路径规划问题能力。

[1] 刘海洋,木仁.基于Floyd算法的公交专用车道设置路段分析[J].中国管理科学,2015(S1):5-8.

[2] 张蓉,陈佳俊,顾向涛,等.智能应急疏散路径规划系统的实现[J].江苏科技大学学报:自然科学版,2016(2):98-103.

[3] Myoupo J F,Fabret A C.A modular systolic linearization of the warshall-floyd algorithm[J]. IEEE Transactions on Parallel & Distributed Systems,1996,7(5):449-455.

[4] Wei D.An optimized floyd algorithm for the shortest path problem[J].Journal of Networks,2010,5(12):1496-1504.

[5] Huang Q R,Cao M.Study on the improvement of floyd algorithm and its application in network plan[J].Applied Mechanics & Materials,2014,64(2):1312-1315.

[6] 叶奇明,石世光.Floyd算法的演示模型研究[J].海南大学学报:自然科学版,2008,26(1):47-50.

[8] 郭强.人数少于任务数的全指派问题的迭代算法[J].计算机工程与应用,2006(4):91-93.

[9] 赵礼峰,梁娟.最短路问题的Floyd改进算法[J].计算机技术与发展,2014(8):31-34.

[10] 林华珍,周根贵.求解最短路问题的一种优化矩阵算法[J].长江大学学报:自然科学版,2007,4(4):14-16.

[11] 赵礼峰,梁娟.最短路问题的Floyd改进算法[J].计算机技术与发展,2014(8):31-34.

[12] 钟茹.路网中关键节点和重要路段的分析研究[D].北京:北京邮电大学,2013.

[13] Ridi L,Torrini J,Vicario E.Developing a scheduler with difference-bound matrices and the floyd-warshall algorithm[J].IEEE Software,2012,29(1):76-83.

[14] 茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2004.

[15] Floyd R W.Algorithm 97 (shortest path)[J].Communications of the Acm,1962,5(6):345-345.

[16] 林华珍,周根贵.求解最短路问题的一种优化矩阵算法[J].长江大学学报:自然科学版,2007,4(4):14-16.

[17] 江建宇.共享腹地港口群集疏运系统智能体仿真研究[D].广州:华南理工大学,2014.

[18] 谢潜,武鹏,周江昕,等.基于Floyd-warshall算法的分布式电源孤岛划分[J].水电能源科学,2015(10):173-177.

[19] 陈世林.协同式空中交通流量管理关键技术及若干算法研究[D].南京:南京航空航天大学,2009.

[20] 岳晓鹏,李慧慧.公园内道路规划的优化方法[J].电子科技,2014,27(2):3-6.

Shortest Path of Urban Traffic Based on the Improved Floyd Algorithm

XU Da，CAI Manchun，CHEN Yue

(School of Cyber Security, People’s Public Security University of China, Beijing 100038, China)

floyd algorithm; shortest path; urban traffic network

2016- 09- 04

国家自然科学基金(61602489)

徐达(1991-)，男，硕士研究生。研究方向：算法和大数据。蔡满春(1972-)，男，博士，副教授。研究方向：密码学和算法。陈悦(1992-)，男，硕士研究生。研究方向：灰色理论。

10.16180/j.cnki.issn1007-7820.2017.07.005

TP301.6

A

1007-7820(2017)07-017-04