改进的混合高斯模型运动目标检测算法
周莉鸿
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
改进的混合高斯模型运动目标检测算法
周莉鸿
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
混合高斯模型中阈值T的合理选择在目标与背景区域的获取过程中占有重要的地位。只有选取合适的值,才可以减少灯光突变和图像闪烁所造成的干扰。针对类间最大对称交叉熵自适应选取算法准确度和精确度,在特征类间的频率和频率分布在类间方面需要进行改进。通过增加小的元素值和信息熵改进类间的频率,以及通过加权方式改进频率分布在类间方面的需要。结果表明,改进的对称交叉熵特征选择方法在背景分类中具有更优异的效果。
混合高斯模型;阈值T;对称交叉熵;特征选择;类间
运动目标检测方法主要有光流法、帧间差分法、背景减除法3大类[1-2]。3种方法中背景减除法应用最为广泛,目前主流的有高斯均值法、时间中值滤波法、混合高斯法、核密度估计法以及视觉背景抽取的方式。在快速变化的场景、动态像素缺失条件下跟踪人体一直是一个图像跟踪的难点[3]。为解决这些问题,采用改进高斯混合模型法进行运动目标检测。在高斯混合模型中阈值T的选择一直是研究的重点。文献[4]中采用粗糙熵来确定阈值T的选取,文献[5]通过迭代计算动态像素参数更新,来补偿丢失的像素特征,减少前景误判现象。文献[6]通过均值更新算法减少误检,文献[5]提出采用类间最大交叉熵自适应选取方式来确定阈值T。针对文献[7]的不足,在特征类间的频率和频率分布在类间方面进行改进,增加小的系数与权重,使该方法在背景与目标分类中取得更好的效果。
1 混合高斯模型
1.1 定义
假设红绿蓝三色通道相互独立[8],用k个高斯分布对每个像素强度进行建模,如果用k个高斯分布描述一个像素的轨迹,一个给定的时刻t的像素值Xt的概率为
(1)
其中,k为概率分布的个数;p(k)为第k个高斯分布先验概率1 (2) 1.2 背景模型更新 初始化:均值矩阵的初始值是第一帧中的每个像素值,方差的值是σ0,权重为1/k。 匹配:用新的像素值Xt与k个高斯分布进行比较,用来更新混合模型[8]。如果Xt与一个高斯均值相似的,那么就认为当前像素与模型是匹配的,则其表达式为 Xt-μi,t<λ∑k (3) 参数更新:如果Xt与第i个高斯分布匹配,则对参数进行更新 (1)则参数更新公式如下 ωi,t=(1-ρ)ωi,t+ρ (4) μi,t=(1-ρ)μi,t-1+ρ·Xt (5) (6) 其中,ρ为更新系数; (2)如果Xt与其余的高斯模型都不匹配,那么其中的均值与方差都不变,只对最小权重的权值ωi,t更新,公式为 ωi,t=(1-ρ)ωi,t (7) (3)如果Xt与任何一个高斯模型都不匹配,那么把当前的像素值概率分布作为均值模型,重新建一个背景模型,具体办法如下面的更新公式 j=arg minωk,t-1 (8) ωj,t=ρ (9) μj,t=Xt (10) ∑j,t=σ0 (11) 其中,σ0=6。 1.3 前景分割 k高斯分布中像素按ω降序进行排列的,其中前B个为背景,B的定义如下 (12) 其中,T为阈值。 文献[6]采用一种类间最大对称交叉熵自适应选取算法,离散分布p,q对称交叉熵的定义为 (13) 由贝叶斯理论可知,最优阈值满足高斯模型被划分到不同类的后验概率差别最大,高斯模型基于后验概率p(C1/k),p(C2/k)的对称交叉熵为 (14) 其中,p1为背景模型类的先验概率;p2是非背景模型类的先验概率;p(k/Ci)是第i类中出现的第k个高斯模型分类的概率;p(Ci/k)第k个高斯模型属于第i类的后验概率。如果在高斯模型与类之间有很大的相关性,也就意味着p(C1/k)变大则相关的p(C2/k)相对变小。 对称交叉熵在阈值选取中得到了广泛的应用,并取得了良好的效果。与信息增益相比,对称的交叉熵不需要考虑特征不出现的情况,大幅减少了不经常发生的罕见的特征的干扰,提高分类效率。虽然对称交叉熵在特征选择上取得了很好的效果,但也存在一定的局限性[9]。 2.1 初步改进 如果特征第k个高斯模型属于其他类Ci(i=1,2),概率为p1,p2,则 (15) 信息越均衡,分布越大。熵的值越大,特征值越小。这种信息熵反映了各类的分布情况下的特征,因为对称交叉熵不考虑这种情况,所以将它们结合起来。初步改进公式如下 (16) 2.2 类间的特征频率 对称交叉熵影响背景类的概率分布,但只考虑特征出现或不出现在背景中,没有考虑在背景中的特征频率。假设ωt和ωq在类Ci中,但很少显示或者不显示在其他类别。如果在Ci类中ωt的发生频率>ωq的发生频率,通过对称交叉熵获得的结果还是相似的。频率越大,特征类在一个或几个类别中的性能越强,特征的权重就越大。因此引入特征频率,去优化对称交叉熵[12]。特征集合是T={ωt,t=1,2,…,k},背景di,j(1≤j≤m)显示在训练样本的类Ci中,m代表类Ci的总数,在类Ci中di,j的频率是tfi,j(ωt),权重αi是 (17) 将权重的最大系数αi和式(16)结合,计算公式如下 D**(1:2,k)=max{αi}×D*(1:2,k),i=1,2 (18) 2.3 类频率分布的算法模型优化 分类能力强,不仅在这一类出现频率大,而且在类中还分布均匀。假设k是类Ci的特征,如果只有集中在几次出现在类Ci,在类Ci中作为背景特征被用是很难的,即使占有很大的概率。因此,在同一种类的不同背景模型中的平均分布更为均匀,该类的性能更为强劲。数学统计样本方差的概念代表了离散样本的程度。特征方差越小,特征的频率越接近类内的背景,即特征的分布更为平均,这些特征在背景模型内具有更强的性能能力,应该在对称的交叉熵模型中增加其权重[13]。 经过上面的分析,提出了一个基于对称交叉熵的频率类间分布的加权模式。类Ci的特征k的样本方差公式如下 (19) 特征频率的样本方差越小,特征的分类能力越强。上述参数进行归一化和校正 (20) 显然,特征值k在类Ci内越平均分布,βi值越大,能力越强。将最大的权重系数βi×αi和式(16)结合,计算公式如下 D***(1:2,k)=max{βi×αi}×D*(1:2,k),i=1,2 (21) 2.4 阈值T选取 为防止对数项奇异化,将式(21)进行改写 (22) 再分别对每个高斯模型的交叉熵求取平均值,将二者的和当做总的类间差异 (23) 假设第k个高斯分布的后验概率服从正态分布 (24) (25) (26) (27) (28) (29) (30) 用贝叶斯公式求取后验概率 (31) 改写式(23) (32) 通过穷尽搜索的方法来获取背景模型选取的最优个数k*,当D***(1:2;k′)取最大值的时的k′即为所求的k*,也就是 (33) 则所求阈值T[14] (34) 背景模型个数选取公式为 (35) 以上方法弥补了混合高斯模型在选取背景模型时考虑决定像素点归属问题的均值和方差对分类影响这一缺陷,也减少了灯光突变和图像闪烁带来的干扰[15]。 3.1 准确性验证 TP表示第k个高斯模型属于背景这一类,并且判断正确,FP表示第k个高斯模型不属于背景这一类,但判断为属于这一类,FN表示是第k个高斯模型属于背景这一类,但判断为属于非背景类。用P表示正确归属分类,R表示错误归属分类,F作为分类结果评估 (36) (37) (38) 结果评估如图1所示。 图1 分类结果评估 通过图1所示,改进的最大类间对称交叉熵让阈值T选取更加合适,使得第k个高斯分布模型归属背景模型类更加准确,提高了算法准确性。 3.2 实时性验证 改进的最大类间对称交叉熵算法与传统最大类间对称交叉熵算法处理每帧视频时间对比如表1所示。视频为30帧每秒,所以处理每帧时间约为34 s。 表1 改进算法与原始算法对比 通过表1可知,改进后的算法虽然提高的幅度并不大,而且有时用的时间超过了传统的方式,但总体来看处理速度上也有所提高。 本文基于高斯混合模型法和改进的最大类间对称交叉熵阈值选取方法,提出了自适应选取算法,通过对对称交叉熵的改进,引入权重和信息熵的概念,使算法处理在准确度和速度上都有一定进步,选取出了最能代表背景的模型作为背景模型,在背景分类中拥有更优异的效果。 [1] 姚敏.数字图像处理[M].北京:机械工业出版社,2006. [2] 刘鑫,刘辉,强振平,等.混合高斯模型和帧间差分相融合的自适应背景模型[J].中国图象图形学报,2008,13(4) :729-734. [3] 崔学超.基于减背景和混合差分的运动目标检测算法[J].电子科技,2010,23(10):85-88. [4] 靳海伟.基于视频的运动目标检测算法研究[D].南京:江南大学,2015. [5] 耿沛,苏晓龙.一种改进高斯模型的人体运动图像跟踪算法[J].计算机仿真,2012,10(10):279-282. [6] 白云飞.嵌入式视频监控系统与自动摔倒检测的实现[D].杭州:中国计量学院,2014. [7] 刘万军,李琳.基于熵理论改进混合高斯模型的运动目标检测算法[J].计算机应用研究,2015,7(7):2226-2233. [8] Olivier B,Marc V D.ViBe: a universal background subtraction algo-rithm for video sequences[J].IEEE Transactions on Image Processing,2011,20(6):1709-1724. [9] Wu Guohua,Wang Liuyang.Improveed expected cross entropy method for text feature selection[C].Beijing:IEEE International Conference on Computer Science and Mechanical Aotomation,2015. [10] 于万霞,杜太行.基于彩色空间的背景帧差法视频车辆检测[J].计算机仿真,2011,27(1):285-288. [11] 杨叶梅.基于改进光流法的运动目标检测[J].计算机与数字工程,2011,39(9):108-110. [12] 刘娣,高美凤.基于背景差分的核密度估计前景检测方法[J].计算机工程与应用,2013,49(6):170-174. [13] 肖斌,汪敏.基于主动轮廓模型的交通场景运动目标提取算法[J].计算机系统应用,2012,21(1):168-172. [14] Elgammal A,Duraiswami R,Harwood D,et al.Back-ground and fore-ground modeling using nonparametric kernel density estimation for visual surveillance[J].Proceedings of the IEEE,2002,90(7): 1151-1163. [15] 方帅,薛方正,徐新和.基于背景建模的动态目标检测算法的研究与仿真[J].系统仿真学报,2005,17(1):159 -161,165. Moving Target Detection Algorithm Based on the Improved Gaussian Mixture Model ZHOU Lihong (School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China) The reasonable selection of thresholdTin the Gaussian Mixture Model plays an important role in acquiring the target and the background region. Only by selecting the appropriate value, can we reduce the interference caused by the lighting mutation and image flicker. According to the class of maximal symmetric cross entropy, the accuracy and precision of the adaptive selection algorithm are improved, and the frequency and frequency distribution between feature classes need to be improved. By increasing the small element value and the information entropy, the frequency of the class is improved, and the frequency distribution is improved by the weighted method. The results show that the improved symmetric cross entropy feature selection method has a better effect in background classification. Gaussian mixture model; thresholdT; symmetric cross entropy; feature selection; between classes 2016- 08- 12 周莉鸿(1991-),女,硕士研究生。研究方向:智能家居。 10.16180/j.cnki.issn1007-7820.2017.07.006 TP301.6;TP391.4 A 1007-7820(2017)07-021-042 阈值T自适应选取及算法改进

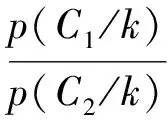


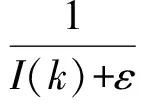
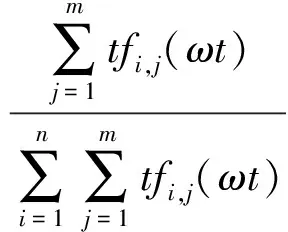


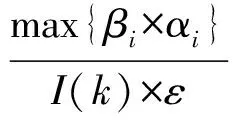

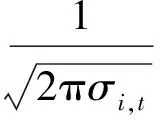

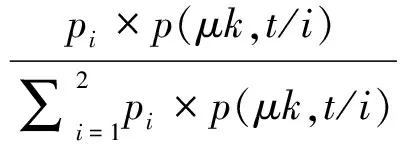


3 实验分析
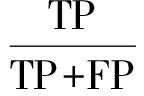

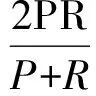
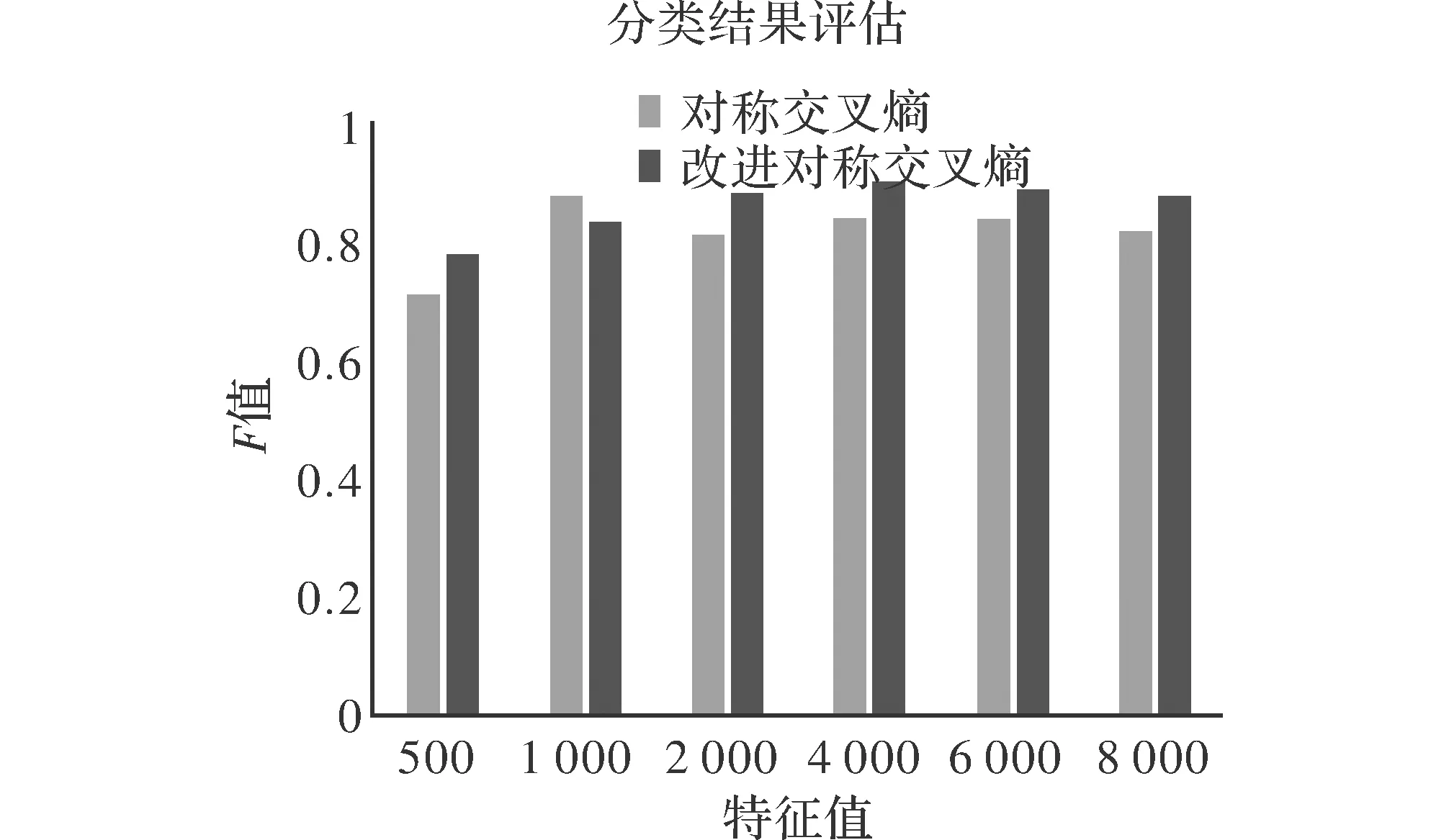
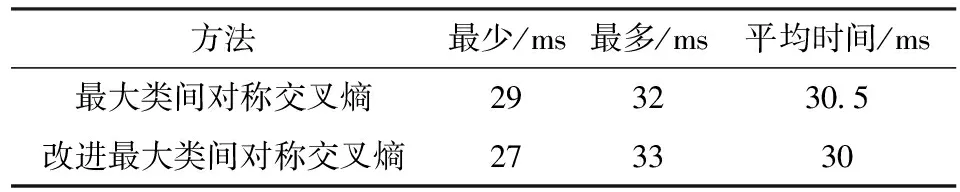
4 结束语

