基于OTSU改进的布匹检测算法研究

解祥新，江小静，刘琴琴，魏 燕

(南通理工学院，江苏 南通 226002)

0 引言

基于阈值分割的布匹疵点检测算法可以大致分为以下几个步骤，首先对采集到的布匹图像进行降噪，消除无关信息，增强细节对比度等[1]，再利用阈值分割算法进行图像分割，最后将得到的分割后的图像进行疵点分类等后续处理。在实际生产中，疵点类型主要以破洞、断经为主[2]，因此本文中所检测的疵点类型基本为破洞、断经。

1 改进最大类间方差法

OTSU全称最大类间方差法，该方法将待检测样本的前景和背景分离开来。本文将素色布匹的正常底纹看作背景，把待检测素色布匹的瑕疵区域看作前景。通过OTSU阈值分割算法把素色布匹瑕疵区域和标准纹理背景信息进行解耦[3]，得出的最佳阈值将布匹瑕疵与纹理背景分割开来，实现瑕疵检测。

最大类间方差算法具有检测周期短和运算速度快等优点[4]，可以满足工业现场的实时检测要求。

传统最大类间方差算法原理：假定待检测的素色布匹图像共有L个灰度级，nq是灰度级为q的像素点个数，则图像灰度级的概率Pq如下式：

(1)

K级灰度以下像素的灰度概率均值和累积值分别是ωk和μk，如式(2)和式(4)所示：

(2)

ω(L-1)=1

(3)

(4)

假设按照灰度阈值T把待检测素色布匹样本图像分为布匹正常底纹和表面瑕疵区域两类：C0类(灰度级为从0到T)，C1类(灰度级为从T+1到L-1)。则C0类和C1类两类的概率公式为式(5)和式(6)所示：

(5)

(6)

两类的均值可以用式(7)和式(8)表示：

(7)

(8)

对于整个图像来说，其灰度均值为式(9)：

μ=μ0ω0+μ1ω1

(9)

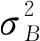
(10)

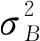
传统的最大类间方差法的缺点：

(1)对于一些灰度级不连续的图像来说，通过传统的最大类间方法所计算出来的阈值很难收敛到全局最优。

(2)若背景图像与前景图像分布差异非常大，那么最大类间方差算法将有可能会失效。

(3)当图像中仅有两种类别时，最大类间方差能够很好地适用；但是当超过两种类别时，就需要改进增加额外阈值，来进行分割。

因此针对以上传统最大类间方差法的缺点进行如下改进：

(1)计算图像灰度级L。计算图像的灰度平均值μT，将μT取整|μT|作为图像的灰度级，即L=|μT|；

(2)给分割次数赋以初始值J=1；

(3)利用最大类间方差法计算图像的像素N、阈值K、阈值选择函数η、类内方差σw；

迭代，N(J)=N;K(J)=K;L=K;η(J)=η;σ(J)=σw;J=J+1;

(4)如果J≤1，那么返回步骤3；若大于1，则计算出ε的值。

(11)

(5)如果ε≥0，那么返回步骤3；若小于0，则查找最大η(J)所对应的阈值，作为最佳阈值K。

2 实验步骤及仿真

本节算法的流程如图1所示。

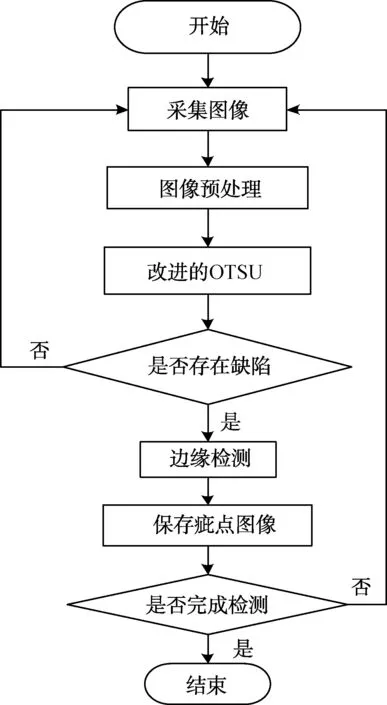
图1 基于改进最大类间方差法的检测算法流程

具体步骤如下：

步骤1：采集现场布匹图像，进行双边滤波处理，经过双边滤波处理之后能够较好的滤除低频信息，减少低频信息的干扰，并且能够很好地保存图像边缘处的细节信息。双边滤波的数学表达式如下：

(12)

其中，(k,l)为模板窗口的中心坐标；(i,j)为模板窗口的其他系数的坐标；σd为高斯函数的标准差。

步骤2：将双边滤波处理后的图像再通过中值滤波滤除斑点噪声及椒盐噪声，中值滤波在降噪的同时也能够有效保存边缘处的细节。用中值滤波处理双边滤波处理后的图像g(i,j)：

G(x,y)=mid{g(x-a,y-b),a,b∈W}

(13)

其中，G(x,y)为进行中值滤波后的二阶矩阵，W为选择的二维模板，选取3×3的区域；

步骤3：将预处理后的图像，利用改进的最大类间方差法进行阈值分割。计算图像灰度级L，计算图像的灰度平均值μT，令L=|μT|；给分割次数赋以初始值J=1；利用最大类间方差法计算图像的像素N、阈值K、阈值选择函数η、类内方差σw；再进行迭代，直到计算出最佳阈值K。

步骤4：分割完成后判断是否存在疵点，如果不存在疵点，则继续采集图像进行疵点检测；若存在疵点，则进行边缘检测，标识出疵点，进行数据保存后，再继续采集图像。

传统最大类间方差法在阈值分割时，并不能很好地将疵点分割出来，而通过改进的最大类间方差法，能够很好地分割出疵点。传统最大类间方差法检测准确率只有78%，而改进后的最大类间方差法检测准确率可达到94%。

3 结语

本文主要研究基于改进最大类间方差法的检测算法。并通过实验仿真分析这种算法在针对无样本的疵点检测上精度高，具有一定的效果。