基于动态多种群的粒子群优化算法

王宇嘉，聂善坤，肖闪丽

(上海工程技术大学 电子电气工程学院，上海 201620)



基于动态多种群的粒子群优化算法

王宇嘉，聂善坤，肖闪丽

(上海工程技术大学 电子电气工程学院，上海 201620)

针对粒子群算法在解决高维非线性优化问题时存在易陷入局部最优的缺陷，文中提出了一种基于动态多种群的粒子群优化算法。该算法根据平均适应度值将种群划分为两个子种群，将低于平均适应度值的个体组成的子种群采用粒子群算法进行更新，其余个体组成的子种群采用自适应混沌粒子群算法进行更新；进化过程中，两个子种群规模根据平均适应度值的变化进行动态调整。标准测试函数的测试结果表明，所提出算法增加了种群的多样性，提高了算法全局搜索性能。

粒子群算法；多种群；自适应；混沌；非线性优化

粒子群算法(Particle Swarm Optimization，PSO )是受鸟群觅食策略的启发而得到的一种智能进化算法[1-2]。与其他进化算法相比，PSO算法具有操作简单、收敛速度快、对目标函数要求少的特点。但是，PSO算法容易过早收敛于局部最优[3]。为增加种群多样性，提高算法全局搜索性能，研究者对PSO算法进行了改进，主要包括：算法参数调节[4-7]、将PSO算法与其他启发式方法相结合等[8-17]。然而，粒子群算法在搜索过程中是非线性且高度复杂的，而惯性权值和加速因子的线性递减策略不能有效地反映算法的搜索过程，且在求解复杂问题的后期容易陷入局部最优。同时，大部分混沌粒子群算法利用Logistic映射生成的混沌序列极不均匀，浪费了大量的计算时间，且不能很好地遍历可行域。另外，量子粒子群算法应用于实际工程时，其在进化后期会因种群多样性降低而出现早熟收敛现象。

为平衡算法的全局搜索能力和局部搜索能力，本文提出了基于动态多种群的粒子群算法(DMPSO)，根据平均适应度值将种群划分为两个子种群，低于平均适应度值的个体组成的子种群采用粒子群算法进行更新，其余个体组成的子种群采用自适应混沌粒子群算法进行更新。进化过程中，子种群规模根据平均适应度值进行动态调整。采用6个Benchmark测试函数对所提出算法进行验证，并与改进的粒子群算法(IAPSO[7]，AIWCPSO[14]，IQPSO[17])进行了比较。

1 粒子群算法

粒子群算法是模拟鸟群的觅食行为得到的一种进智能化算法。假设整个鸟群为没有质量的粒子，并将粒子的搜索空间扩展为N维。设定每个粒子的位置为xi=[xi1,xi2,…,xiN]，粒子的移动速度为vi=[vi1,vi2,…,viN]，则粒子在搜索过程中的速度和位置更新为

(1)

(2)

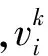
2 基于动态多种群的粒子群算法

2.1 种群划分策略

为提高算法的全局搜索能力，本文在采用动态多种群粒子群算法增加种群的多样性，该算法根据平均适应度值将种群划分为两个子种群，低于平均适应度值的个体组成的子种群采用粒子群算法进行更新，其余个体组成的子种群采用自适应混沌粒子群算法进行更新。算法在前期可以保证种群的多样性，提高算法的全局搜索能力；算法后期可在极值点附近进行更精细的局部搜索，提高收敛速度。

2.2 学习参数调整策略

自适应混沌粒子群算法的惯性权值的更新公式[18]为

(3)

其中，fi为当前粒子的适应度值；fmin为种群的最小适应度值；favg为种群的平均适应度值；wmin为惯性权值的最小值；wmax为惯性权值的最大值。

在自适应混沌粒子群算法中，为增加算法的全局搜索能力，在性能较好的粒子周围引入了混沌搜索的思想。粒子的混沌搜索位置为

(4)

其中，zj,k∈[-1,1]为Logistic映射函数[19]生成的混沌搜索因子，调整其生成公式为

zj,k+1=μzj,k(1-|zj,k|)

(5)

其中，μ=4且|zj,k|≠{0,0.25,0.5,0.75,1}。

在混沌搜索的前期，为跳出局部极小值，粒子的位置变化较大，则邻域半径η的值需要较大。当接近最优解时，η的值需要较小，则η的值为

ηi=γ[(kmax-c_k+1)/kmax]2xi

(6)

其中，γ为邻域半径(本文取0.1)；kmax为混沌搜索的最大次数；c_k为混沌搜索的当前次数。

粒子群算法的惯性权值的更新公式如下

w=wmin+(wmax-wmin)×iter/MaxIter

(7)

其中，iter为算法的当前迭代次数；MaxIter为算法的最大迭代次数。

考虑到种群的全局最优位置对个体运动的影响，对子种群一的个体采用更新公式

vj+1=ωvj+c1r1(pbj-xj)+c2r2(pg1-xj)
+c3r3(pg-xj)

(8)

其中，c3为加速常数，取1.49；r3为[0,1]区间的随机数；pg1为子种群一的全局最优位置。

为保证算法的多样性，以及减弱最优位置对子种群二的个体的影响，对该子种群采用速度更新公式

vj+1=ωvj+c1r1(pbj-xj)+c2r2(pg2-xj)
+(2-c3)r3(pg-xj)

(9)

2.3 算法流程

动态多种群粒子群算法的实现的具体步骤如下：

步骤1 设置种群参数；

步骤2 初始化种群；

步骤3 计算粒子的适应度值，并得到种群的个体最优位置pb和主种群的全局最优位置pg；

步骤4 计算粒子群的平均适应度值，划分子种群；

步骤5 选取子种群一的全局最优位置Gb1根据式(2)、式(7)和式(8)对子种群一进行更新；

步骤6 选取子种群二的全局最优位置Gb2，根据式(4)～式(6)对子种群二进行混沌搜索，并根据式(2)，式(4)和式(9)对子种群二进行更新；

步骤7 将步骤5和步骤6得到的子种群重组为新的种群，并计算粒子的适应度值；

步骤8 更新种群的个体最优位置和主种群的全局最优位置；

步骤9 判断是否满足进化终止条件，若不满足则返回步骤4；若满足，则算法终止。

3 仿真实验

3.1 测试函数

为测试DMPSO算法对粒子群算法搜索性能的改善，采用6个典型的测试函数对算法进行仿真实验。测试函数如表1所示。

表1 测试函数

3.2 结果与分析

为保证实验结果的准确性与有效性，对算法进行50次独立实验，并对50次独立运行的结果进行统计，计算4种算法的最优值(Best)，最差值(Worst)，平均值(Mean)和均方误差(St. Dev)。其中最优值和最差值是用于评判算法的寻优能力，平均值和均方误差是用于评判算法的稳定性和可重复性。表2所示为4种算法的实验结果。

表2 测试结果

如表3所示，DMPSO算法在6个测试函数上的测试结果与目标值之间误差较小，并且在最优解、最差解、平均值和均方误差上的精度较高。IQPSO算法在测试函数f2上的测试结果与目标值之间误差较大，但在其余测试函数上，与目标值之间的误差较小。AIWCPSO算法在测试函数f2和f5上最优解与目标值之间误差较大，但在其他指标和其余测试函数上，其测试结果与目标值之间误差次于IQPSO算法。IAPSO算法在6个给出的测试函数上的测试结果与目标值之间误差较大，但两者之间差异不是太大。

由此可知，本文提出的DMPSO算法在6个Benchmark测试函数上的测试结果，在最优值、最差值、平均值、均方误差方面均明显优于其他3种算法。因此，本文提出的DMPSO算法能够增强算法的勘探开采能力，提高算法搜索全局最优解的能力，增强了算法跳出局部最优的能力。

在DMPSO算法中，子种群的规模随着迭代次数而变化。图1 所示为测试函数f4对DMPSO算法进行测试的过程中，各子种群的规模变化曲线。为便于区别，将采用粒子群算法进行更新的子种群记为子种群1，将采用自适应混沌粒子群算法进行更新的子种群记为子种群2。

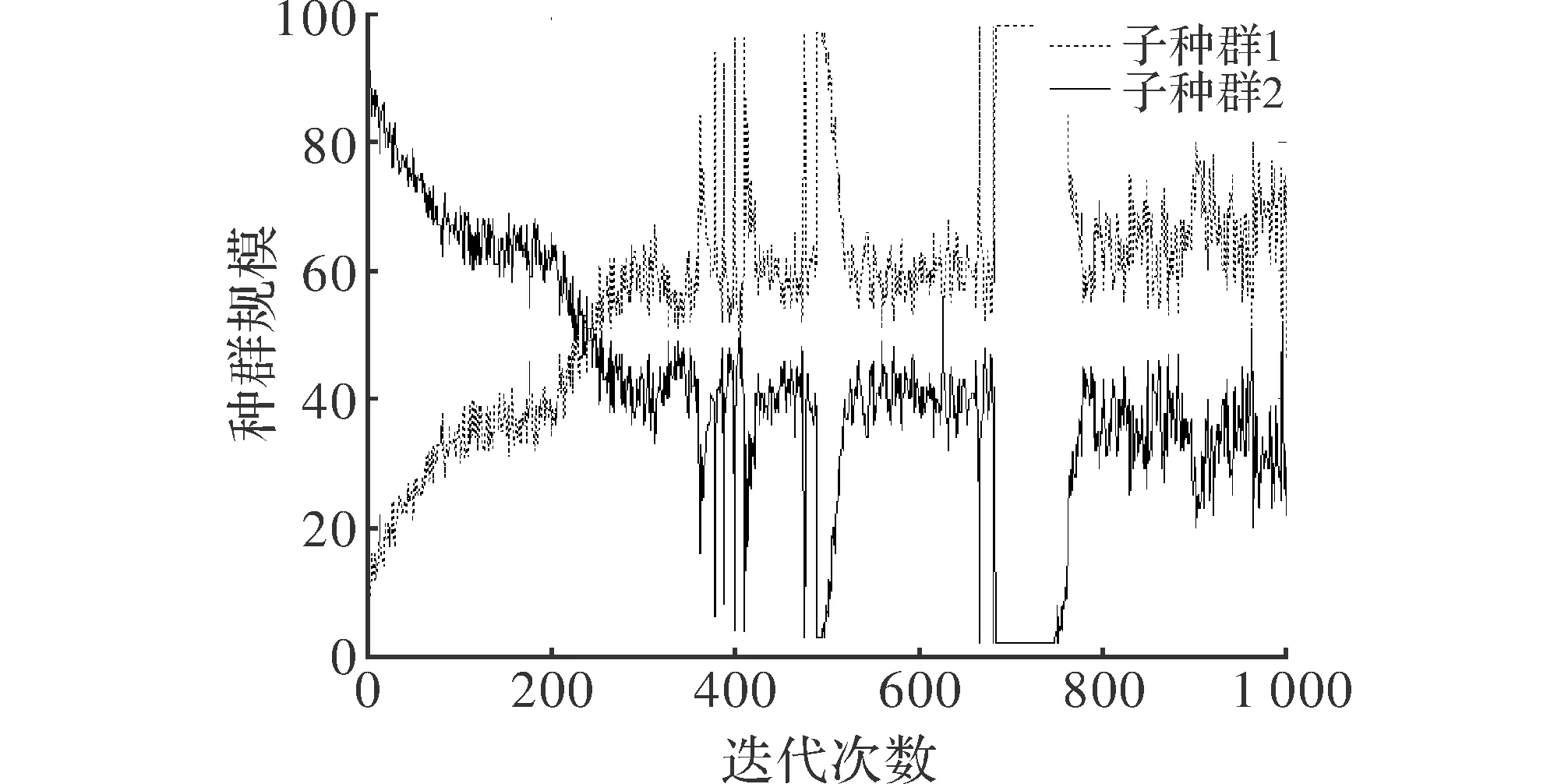
图1 各子种群规模变化曲线

如图1所示，在算法的运行过程中，各子种群的规模随着粒子适应度值的改变而发生变化。种群多样性表征了群智能算法在进化过程中的运行信息。选择较为合理的观测方式来表征群体的多样性对了解算法的运行信息以及增加算法的勘探开采能力具有着重要的意义。本文中选取文献[13]中的早熟收敛程度评价指标Δ来表征算法的多样性，Δ值越大，则种群多样性越好，反之越差。其公式为

(11)

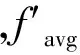
图2所示为测试函数f1对4种算法进行测试的过程中，种群多样性的变化曲线。

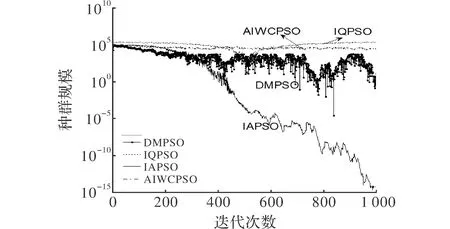
图2 种群多样性变化曲线

如图2所示，在多样性方面，DMPSO算法的种群多样性次于IQPSO算法和AIWCPSO算法；在迭代次数为400～600阶段，AIWCPSO算法的种群多样性优于IQPSO算法，其余时刻两者差异不大。IAPSO算法的种群多样性较差，次于DMPSO算法。图3所示为6个测试函数对4种算法进行测试的过程中，全局最优解随迭代次数的变化曲线。

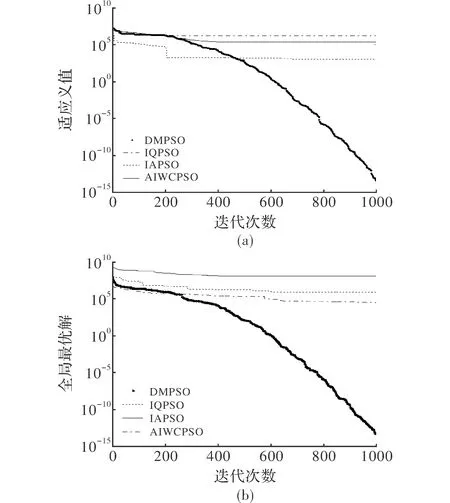
图3 全局最优解变化曲线

从收敛精度方面看，DMPSO算法搜索到的全局最优解在测试函数上均明显优于其他3种算法。在测试函数f3上，AIWCPSO算法搜索的全局最优解仅次于DMPSO算法，但优于其他3种算法；在测试函数f1上，IAPSO算法的全局最优解优于AIWCPSO算法，但次于IQPSO算法。由此可知，与其他3种算法相比，本文提出的DMPSO算法在解决高维非线性优化类问题上具有较好的全局搜索能力。

4 结束语

针对粒子群算法在解决高维非线性优化问题时易陷入局部最优的问题，本文提出了一种动态多种群粒子群优化算法。采用6个Benchmark测试函数对所提出算法进行了验证，同时将算法IQPSO， IAPSO，AIWCPSO算法进行了比较。仿真实验表明，本文提出的DMPSO算法能够动态地调整子种群的规模，并增加了种群的多样性。在解决高维多峰函数的寻优问题上，较IAPSO、IQPSO、AIWCPSO算法而言，DMPSO算法的寻优能力和跳出局部最优具有较为明显的改善，提高了算法在寻优解上的收敛精度，增加了算法在跳出局部极小值上的能力。

[1] Kennedy J,Eberhart R.Particle swarm optimization[C].MA,USA:IEEE International Conference on Neural Networks,1995.

[2] Farrell H,Newman A L.A modification to particle swarm optimization algorithm[J].Engineering Computations,2002,19(8):970-989.

[3] 吴方劼,张承学,段志远.基于动态多种群粒子群算法的无功优化[J].电网技术,2007,31(24):35-39.

[4] Shi Y,Eberhart R C.Empirical study of particle swarm optimization[C].California:Proceedings of the 1999 Congress on Evolutionary Computation,1999.

[5] 李聪,宋文龙.一种基于适应值分析的智能粒子群算法[J].计算机与现代化,2015(5):21-24.

[6] Hua X,Hu X,Yuan W.Research optimization on logistics distribution center location based on adaptive particle swarm algorithm[J].Optik - International Journal for Light and Electron Optics,2016,127(20):8443-8450.

[7] Chaudhary N,Raj R,Kiran K,et al.Improved asynchronous PSO based design of multivariable PID controller[C].Passdina:International Conference on Control,Automation,Robotics and Embedded Systems, 2013.

[8] 吴晓军,薛惠锋,李慜,等.GA-PSO混合规划算法[J].西北大学学报:自然科学版,2005,35(1):39-43.

[9] 高尚,杨静宇,吴小俊,等.基于模拟退火算法思想的粒子群优化算法[J].计算机应用与软件,2005,22(1):103-104.

[10] 支成秀,梁正友.融合粒子群优化算法与蚁群算法的随机搜索算法[C].南宁:广西计算机学会2006年会,2006.

[11] 高尚,杨静宇.混沌粒子群优化算法研究[J].模式识别与人工智能,2006,19(2):266-270.

[12] 殷丽娟,赵熙临,梅真.基于混沌粒子群优化算法的微电网优化运行技术[J].电力系统及其自动化学报,2016(5):191-195.

[13] 高雷阜,刘旭旺.一种基于混沌的自适应粒子群全局优化方法[J].计算机工程与应用,2010,46(3):51-53.

[14] Zhang Y,Zhao Y,Fu X,et al.A feature extraction method of the particle swarm optimization algorithm based on adaptive inertia weight and chaos optimization for Brillouin scattering spectra[J].Optics Communications,2016,37(6):56-66.

[15] Sun J,Fang W,Wang D,et al.Solving the economic dispatch problem with a modified quantum-behaved particle swarm optimization method [J].Energy Conversion and Management,2009(50):2967-2975.

[16] Haddar B,Khemakhem M,Hanafi S,et al.A hybrid quantum particle swarm optimization for the Multidimensional Knapsack Problem[J].Engineering Applications of Artificial Intelligence,2016(55):1-13.

[17] 冯仲恺,廖胜利,牛文静,等.改进量子粒子群算法在水电站群优化调度中的应用[J].水科学进展,2015,26(3):413-422.

[18] 司风琪,顾慧,叶亚兰,等.基于混沌粒子群算法的火电厂厂级负荷在线优化分配[J].中国电机工程学报,2011,31(26):103-109.

[19] He Y,Xu Q,Yang S,et al.Reservoir flood control operation based on chaotic particle swarm optimization algorithm[J].Applied Mathematical Modelling,2014,38(17-18):4480-4492.

A dynamic Multi-group Particle Swarm Optimization

WANG Yujia，NIE Shankun，XIAO Shanli

(School of Electronic and Electrical Engineering, Shanghai University of Engineering Science,Shanghai 201620, China)

The particle swarm optimization has been known to suffer from the local minimal. In order to overcome this drawback, a dynamic multi-group particle swarm optimization is proposed, by which the main swarm is divided into two subgroups according to the average value of the fitness value of these particles. The subgroup with a good performance is based on the particle swarm optimization, while the other is based on an adaptive chaos particle swarm optimization. During the evolution, the size of each subgroups is dynamically adjusted according to the change of the average value of the fitness. The proposed algorithm is tested on six benchmark functions to confirm the feasibility of the proposed algorithm. The experimental results demonstrate that the proposed algorithm has the ability to avoid being trapped in the local minimal and improves the ability of the global optimization.

particle swarm optimization; multi-group; adaptive; chaos; nonlinear optimization

2016- 08- 23

国家自然科学基金(61403249); 上海市自然科学基金(10ZR1314000)

王宇嘉(1979-)，女，博士，副教授。研究方向：智能控制方向等。聂善坤(1991-)，男，硕士研究生。研究方向：智能控制等。

10.16180/j.cnki.issn1007-7820.2017.07.003

TP301.6

A

1007-7820(2017)07-009-05