基于基站定位数据的地图匹配研究

郝晓平，李 烨

(上海理工大学 光电信息与计算机工程学院，上海200093)



基于基站定位数据的地图匹配研究

郝晓平，李 烨

(上海理工大学 光电信息与计算机工程学院，上海200093)

针对目前基于基站定位数据的地图匹配单点误差大、匹配率低、搜索空间大、耗时严重等问题，文中利用滤波技术对基站定位数据预处理，有效降低地图匹配后的单点误差。通过将基站定位区域的OpenStreetMap路网数据网格化，大幅减少了候选匹配点的搜索空间与耗时，同时利用隐马尔科夫模型的维特比算法大幅度提高了路段匹配率。该方法对今后利用基站定位数据进行用户行为分析、电子导航等提供了应用基础。

地图匹配；基站定位；隐马尔科夫模型；维特比算法

当前，业界针对地图匹配的研究主要以GPS定位为主，基于GPS定位数据的地图匹配研究起步较早，技术上比较成熟，而基于基站定位数据的地图匹配研究较少[1-2]。文献[3]通过对移动终端在通信网络中切换变化模式的研究来推断终端在现实环境中的路网的变化模式，以此实现基站定位数据的匹配，但该方法需要维护大量的路网标定数据，耗时严重，且在复杂路段出现较大偏差。文献[4]利用终端在移动过程中连接的每个基站位置坐标来确定终端所在的路段，由于只使用了单个基站的定位数据，所以地图匹配结果差。这两种方法在利用基站定位数据进行地图匹配时，忽略了现实的路网数据对地图匹配结果的影响，且在匹配过程中会对全区域的候选路段进行搜索，耗时严重，效率不高。

本文通过对基站定位算法以及地图匹配理论的研究，首先利用角度滤波技术和均值滤波对基站定位数据进行预处理，这样可以减小地图匹配的单点误差，然后将下载区域的OpenStreetMap(OSM)路网数据网格化，在每一个栅格内寻找候选路段，大幅提高了搜索效率。通过隐马尔科夫模型的维特比算法[5-7]，完成了基站定位数据的匹配工作，并有效提高了路段匹配率。

1 基于基站定位数据的地图匹配研究

本文实现的基于基站定位数据的地图匹配流程如图1所示。

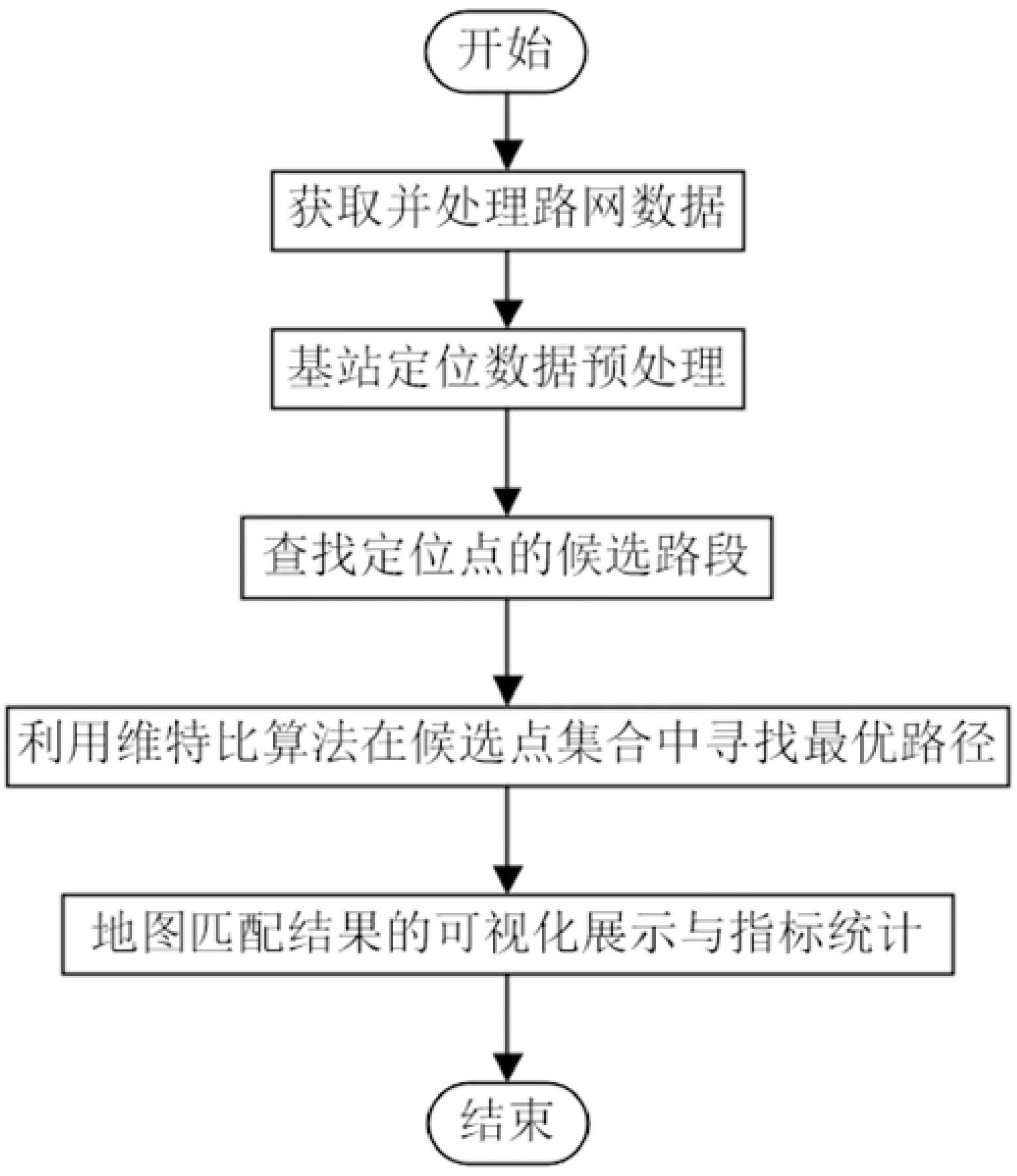
图1 基站定位数据的地图匹配流程图

1.1地图数据处理

在利用基站数据进行地图匹配时，本文采用的是将基站定位数据与实际路网数据相结合的策略。路网数据来源于OSM，数据的存储格式为XML(eXtensible Markup Language)，地图数据处理流程如下：

(1)解析路网数据，解析从OSM下载的XML格式的地图数据，解析出来的地图数据主要包括该块地图区域的Bounds边界信息、Node要素和Way要素；

(2)地图网格化，对目标道路网区域经纬度的最大范围，建立一个长方形区域作为基准进行网格划分，建立该区域的网格索引，通过网格索引能够快速确定候选路段，提高地图匹配效率[8-9]；

(3)获取路网数据的拓扑结构，路网的拓扑结构是电子地图的重要组成部分，主要包括路段的拓扑关系和节点-路段的拓扑关系。一个路段由一个起点和一个终点组成，遍历所有路段的起点和终点，根据路段的拓扑关系可以获得所有节点之间的拓扑关系。

1.2 基站定位数据预处理

由于基站定位数据偏差大、噪声高，使得运用于GPS定位的地图匹配算法不能直接在基站定位数据中使用，所以在地图匹配前，需要对数据进行预处理，预处理步骤如下：

(1)去除不可能点，不可能点主要包括以下情况：1)定位数据中的错误与无效数据，例如数据格式错误、或者定位坐标超出路网区域边界的数据；2)相邻两个定位点的距离超出了移动终端在采集数据的时间间隔内移动的最大距离，则这两个相邻的定位点都为不可能点。相反，如果小于移动终端移动的最小距离，则后面的那个为不可能点；

(2)角度滤波。是针对平面图形光滑处理的一种方法，可以达到良好的去噪效果，能较好地保持曲线的形状。本文利用角度滤波来去除移动终端基站定位数据中的噪声点，其原理如图2所示，假设A、B、C、D为4个按时间顺序相连的基站定位点，它们的坐标分别为(xA,yA)，(xB,yB)，(xC,yC)，(xD,yD)，则可以求出a，b，c，d的长度，再根据三角形余弦定理公式(1)可求出角B和角C的值，如果角B和角C都小于设定的角度阈值，则点C为噪声点，删除点C的数据记录

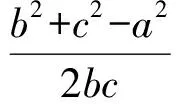
(1)

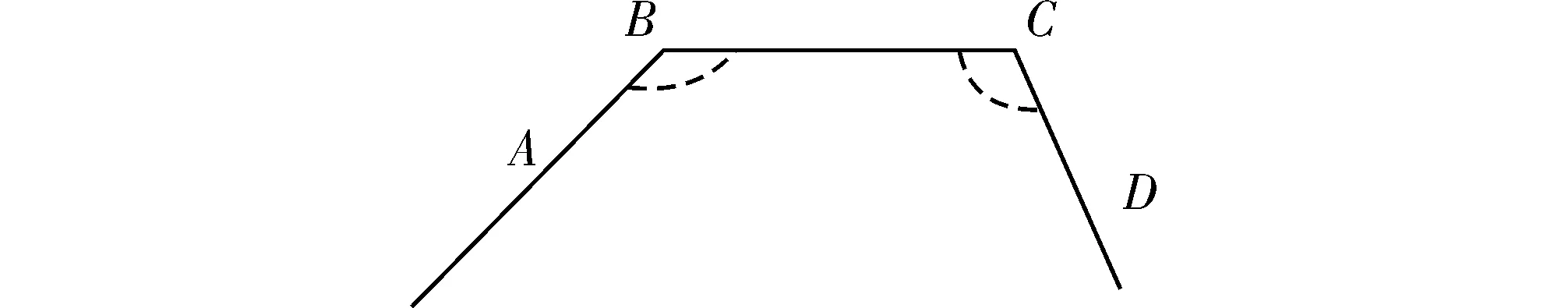
图2 角度滤波示意图

(3)切尾均值滤波。切尾均值是指在一个数列中，去掉数列两端的极端值之后所计算出来的算术平均数，它综合了均值和中位数两种计量方法的优点[10]。本文用切尾均值的方法对移动终端的基站定位数据进行平滑滤波处理，具体的计算如式(2)所示

(2)

其中，iLength为切尾均值的数列长度；iDeleteNum为数列单端切去的个数。当iDeleteNum=0时，切尾均值等于均值；当iDeleteNum接近iLength/2时，切尾均值接近于或是等于中位数。

1.3 获取基站定位点的候选匹配点

基站定位数据经过预处理之后，肯定都在所下载的地图区域内，根据待匹配点的经纬度坐标可以计算出待匹配点所在的经纬网格索引，然后选取以该网格为中心的3×3网格为查找对象，待匹配点查找到周围3×3网格内的所有候选道路之后，由待匹配点向所有候选路段做垂线，垂线与候选路段的交点即为待匹配点在该条路段上的候选点，以待匹配点为中心，以r为搜索半径，如果待匹配点到候选路段的垂直距离>r，则删除该条候选路段，其原理如图3所示。

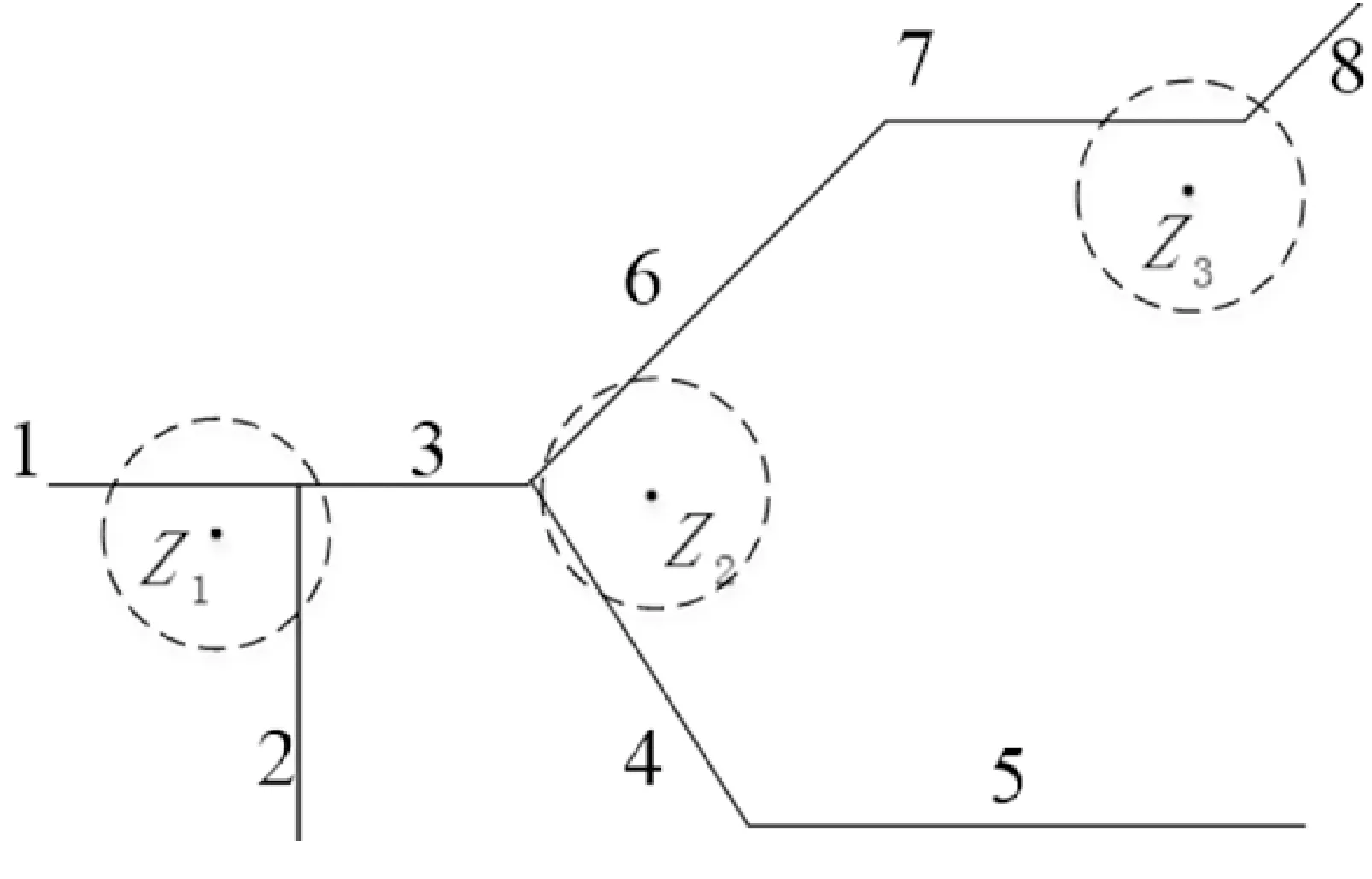
图3 获取基站定位点的候选匹配点

1.4 维特比地图匹配算法

隐马尔科夫模型(Hidden Markov Model，HMM)是一种能够有效地平滑整合噪声数据和路径的算法。

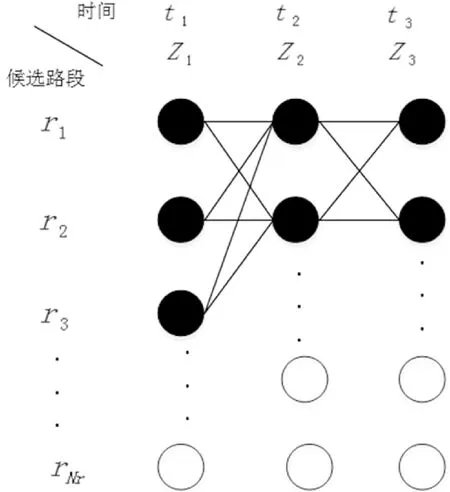
图4 基于隐马尔科夫的地图匹配算法

在图4中，HMM可以观察到的状态是某一时刻基站定位点的坐标值，记为zt，离散状态是所有的候选路段，记为ri，其中i=1,2,…,Nr，例如当t=1时，z1附近有3条候选路段；当t=2时，从z1的3条候选路段上最近的点到z2有两条候选路段。HMM通过可观测到的定位点的坐标及每个t时刻获取的候选路段组成一个道路网，其目标是找出路网中移动终端行驶过的最可能的路径。

HMM由一个三元组(π,A,B)组成，三元组中的参数分别表示初始概率、转移概率和测量概率，在地图匹配中，三元组的含义及其计算方式如下：

(1)初始概率及测量概率。匹配概率指定位点zt匹配到其候选路段ri上的概率，记为P(zt|ri)。初始概率πi指t=1时刻，定位点z1从其候选路段中找出移动终端所在路段的概率[11]。

如图5所示，zt在候选路段r1，r3上的匹配点为Xt,1，Xt,3，zt+1在r2上的匹配点为Xt+1,2。对于正确匹配来说，基站对移动终端进行定位时存在的误差导致了定位点和候选点之间的误差。在本研究中，将定位误差近似为零均值高斯误差[12]，则

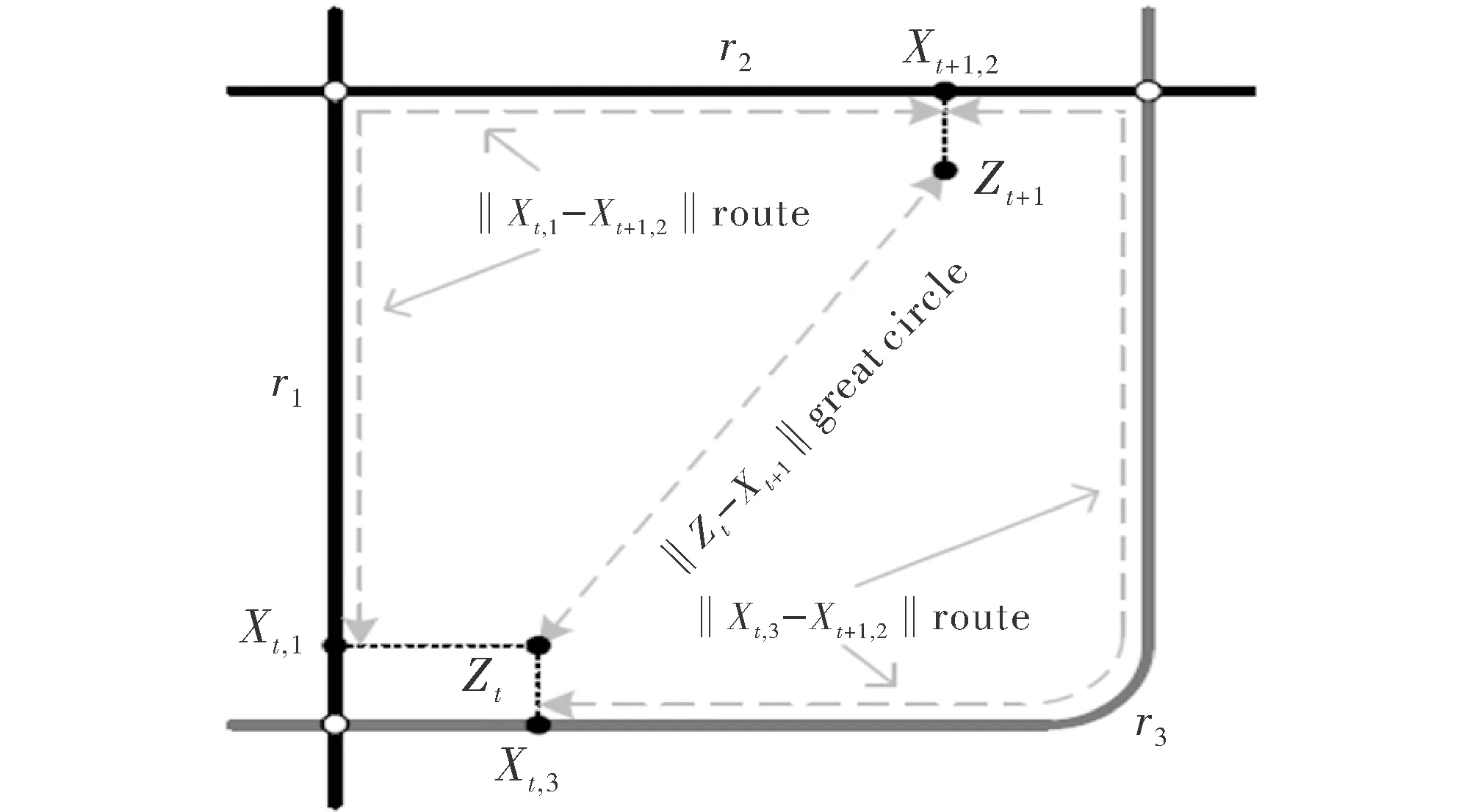
图5 定位点在候选路段上的候选匹配点示意图

(3)

其中，σz为定位测量值的标准差;‖zt-xt,i‖great_circle为定位点与候选点之间的地球表面上的大圆距离，距离越小，则计算出来的测量概率就越大，表明定位点匹配到该候选路段上的概率就越大；

(2)道路转移概率。转移概率是指移动终端从t时刻移动到t+1时刻候选路段之间的转移概率，记为p(dt)。通过比较两个定位点的路径距离和大圆距离可以判断道路是否发生转换，两个距离越接近越能达到正确匹配。通过分析正确匹配的大圆距离和路径距离差的绝对值，发现转移概率呈指数分布[13]

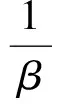
(4)

(5)

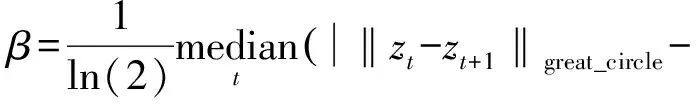
(6)

其中，dt是正确匹配的大圆距离和路径距离差的绝对值，β是距离差的绝对值的中位数，i*和j*指的是行驶路线的真实道路段，e取2.718 282。

利用维特比算法实现地图匹配的主要步骤如下：

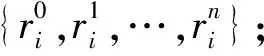
(4)根据基站定位点的观察序列，利用维特比动态规划算法[14]求解最可能候选道路序列，最终的道路序列即为地图匹配的结果。

2 实验结果

本实验所用到的路网数据来自OSM网站，路网区域经度跨度为东经108.91°～108.97°，纬度跨度为北纬34.255°～34.285°。移动终端在该路网区域内按照计划好的路线行驶，对基站定位数据与GPS定位数据进行每秒一次的连续采集，分别收集2 000个带有时间戳的GPS定位经纬度对和基站定位经纬度对，将两种定位数据转换为GPX格式轨迹数据之后导入JOSM(Java Open Street Map)中，如图6所示。

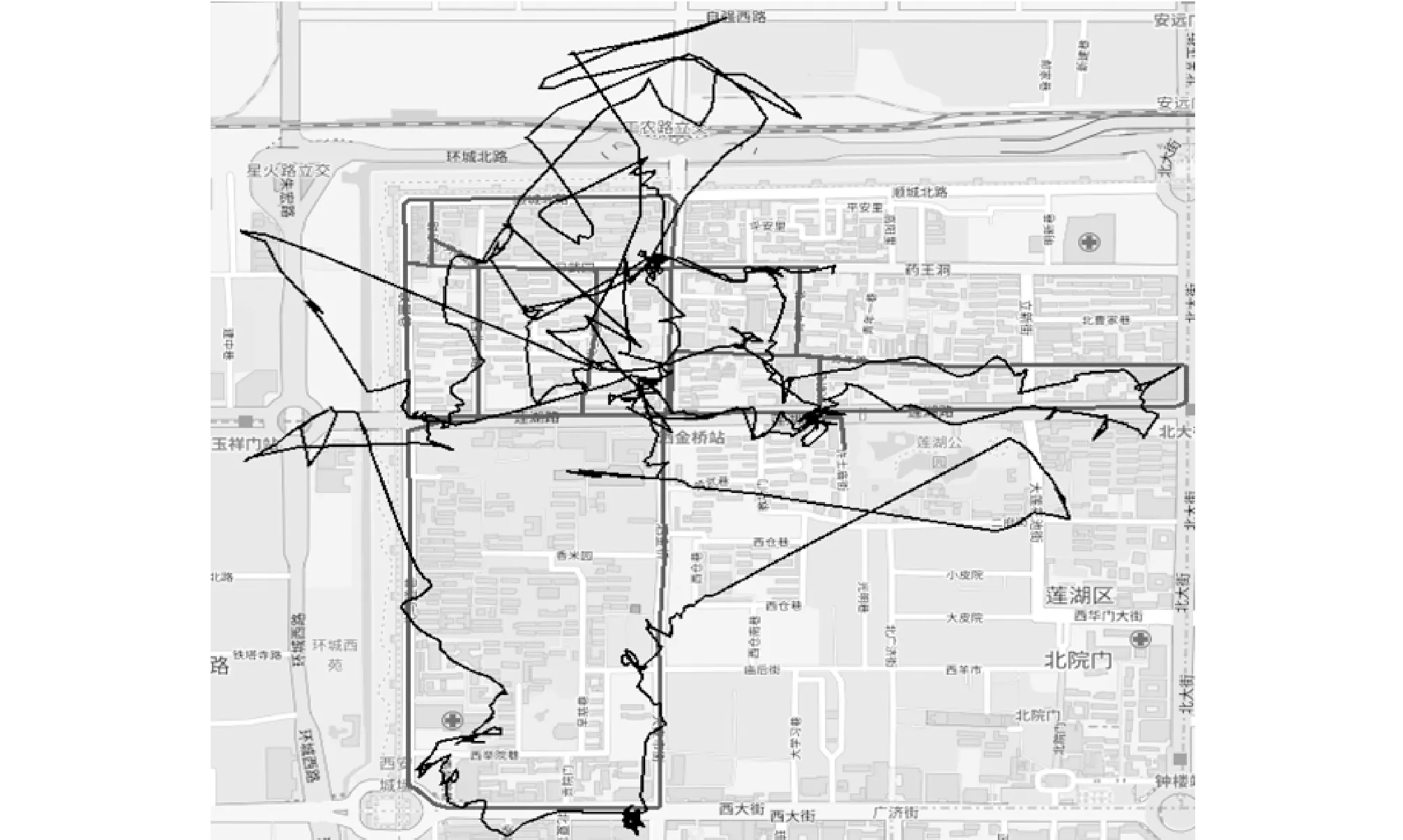
图6 原始基站定位数据与GPS数据轨迹图

图6中，较粗的轨迹为GPS定位轨迹数据，与真实的行驶路线基本完全一致。因此，本文以GPS定位数据为基准来衡量基站定位数据的地图匹配效果。而较细的轨迹为基站定位轨迹数据，从直观上就可以看出基站定位数据的误差较大，无法判断行驶轨迹。

本文通过地图匹配前后基站定位数据的平均定位误差与目标道路匹配率[12]两个指标来衡量匹配效果的好坏。

目标道路匹配率指的是匹配到正确道路上的路段个数与移动终端实际走过的总的路段个数比。计算如式(7)所示

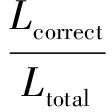
(7)

其中，Lcorrect表示匹配到正确道路上的路段数；Ltotal表示移动终端实际走过的总的路段个数。

将基站定位轨迹数据修复之后的效果与原始的基站定位数据和GPS定位数据的对比如图7所示。

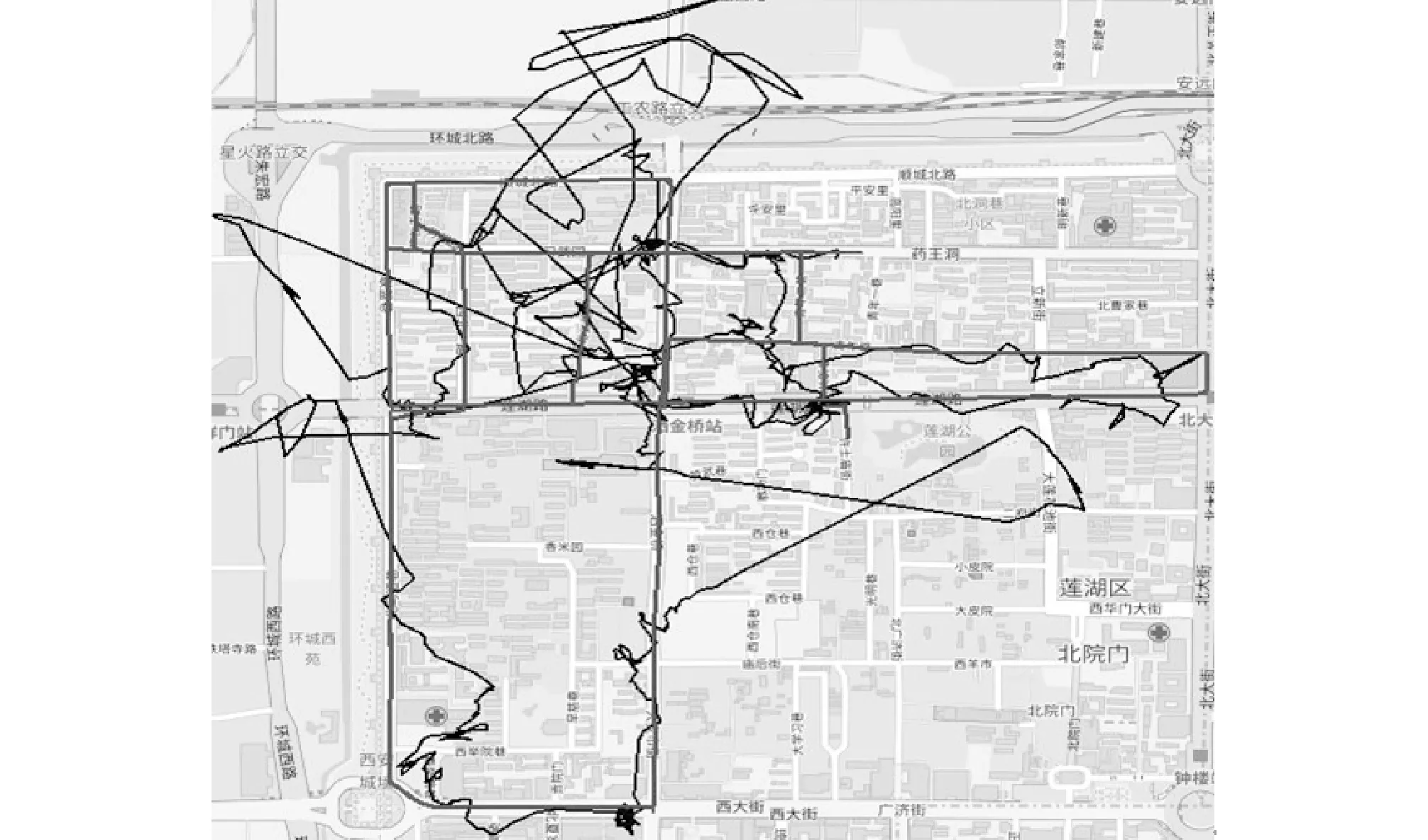
图7 原始基站数据、GPS数据与匹配后的基站数据轨迹图

图7中，较细的轨迹为地图匹配后的基站轨迹数据，较粗的为原始GPS轨迹数据。从图中可以看出，基站定位数据已基本匹配到正确的道路上，对结果进行统计发现，经过地图匹配后的基站定位数据的平均定位误差为56 m，相对于原始数据150 m的定位误差，提高了100 m，并且路段匹配率达到75.9%，比文献[15]中40%的结果要好。

3 结束语

本文通过滤波技术对基站数据的预处理，显著降低了地图匹配后定位数据的单点误差，利用网格化技术有效缩小了候选路段的搜索时间，并通过构建隐马尔科夫模型，利用维特比算法提高了匹配率。本文实现的地图匹配方法在可应用于提高基站定位精度、修复移动轨迹、挖掘用户行为等，具有广阔的应用前景。

[1] 刘兴权,金美含.地图匹配算法综述[J]. 科技信息,2014(4):64-65.

[2] Quddus M A,Ochieng W Y,Noland R B. Current map-matching algorithms for transport applications:State-of-the art and future research directions[J]. Transportation Research Part C Emerging Technologies,2007,15(5):312-328.

[3] 杨飞,惠英.基于手机切换变化模式的道路匹配方法[J].系统工程,2007, 25(11):6-13.

[4] 范秋明,何兆成.基于手机基站定位数据的地图匹配研究[J].交通信息与安全,2011,29(4):52-57.

[5] Assam R,Seidl T.Effective map matching using curve tangents and hidden markov model[C].TX,USA:International Conference on Mobile Ad-Hoc and Sensor Networks,IEEE,2014.

[6] 张鹏飞,申彦明.基于手机位置信息的地图匹配算法[J].计算机应用,2015(s2):294-297.

[7] Wei H,Wang Y,Forman G,et al.Fast Viterbi map matching with tunable weight functions[C].CA,USA:International Conference on Advances in Geographic Information Systems,ACM,2012.

[8] 徐松杰,陈紫强.基于网格分块的快速地图匹配算法[J].桂林电子科技大学学报,2014(1):33-36.

[9] 吴伟,吴堑虹,邓吉秋.基于四级网格划分的待匹配路段初筛方法研究[J].国土资源遥感,2012,24(4):26-29.

[10] 龚昌来.基于数据融合技术的图像均值滤波算法[J].微计算机信息,2007, 23(18):313-314.

[11] Koller H,Widhalm P,Dragaschnig M,et al. Fast hidden Markov model map-matching for sparse and noisy trajectories[C].Moskov:International Conference on Intelligent Transportation Systems,IEEE,2015.

[12] 陈元元,姚佩阳.基于TOA的传感器网络定位误差几何分布研究[J].通信技术, 2009,42(10):63-65.

[13] Jagadeesh G R,Srikanthan T. Probabilistic map matching of sparse and noisy smartphone location data[C].Span: International Conference on Intelligent Transportation Systems,IEEE,2015.

[14] Viterbi A J.Error bounds for convolutional codes and an asymptotically optimum decoding algorithm[J].IEEE Transactions on Information Theory,2015,13(2):260-269.

[15] 何兆成,陈展球,范秋明,等.基于手机基站数据的混合地图匹配算法研究[J]. 交通运输系统工程与信息,2014,14(3):34-42.

Research on Map Matching Based on Base Station Location Data

HAO Xiaoping,LI Ye

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China)

At present, the base station location data map matching suffers great single point error, low matching rate, large search space, and time consumption. This paper uses the filtering technology of data pretreatment of base station positioning to effectively reduce the error of single point map after matching, and the OpenStreetMap network data grid base station location area to greatly reduce the number of candidates the matching point of the search space and time consuming, while using the Viterbi algorithm to greatly improves the Hidden Markov Model section matching rate. This method provides the basis for the application of base station positioning data for user behavior analysis, electronic navigation and so on.

map matching; base station location; hidden Markov model; Viterbi algorithm

2016- 02- 17

沪江基金(C14002)

李烨(1974-)，男，高级工程师。研究方向：工业控制与监测等。郝晓平(1991-)，女，硕士研究生。研究方向：数据挖掘和机器学习。

10.16180/j.cnki.issn1007-7820.2017.07.001

TN927+.21

A

1007-7820(2017)07-001-04