色散系数可调的球KdV方程精确衰减孤波解

李向正,王 飞,张金良

(河南科技大学 数学与统计学院,河南 洛阳471023)

色散系数可调的球KdV方程精确衰减孤波解

李向正,王 飞,张金良

(河南科技大学 数学与统计学院,河南 洛阳471023)

根据简化齐次平衡原则，导出了一个由齐次方程的解到一个可变色散系数的球KdV方程解的非线性变换。该齐次方程容许有指数函数形式的解，通过非线性变换，获得了可变色散系数的球KdV方程的精确衰减单孤波解和双孤波解。

球KdV方程；简化齐次平衡原则；精确衰减孤波解

0 引言

空间或等离子实验室中的离子声波,尤其是离子声孤波的非线性传播受到了较多的关注,并被广泛研究[1]。 多种因素如离子温度、离子梯度密度、外部稳恒磁场、斜传播等对离子声孤波结构的影响都被研究过，但这些研究限定于无界平面几何中，不符合实验室装置或空间的现实。近年来，对离子声波或尘埃离子声波的理论研究表明，在有界的柱体/球体中孤波的性质与无界平面几何中有很大不同。文献[1]利用标准的约化扰动法导出了耗散的柱/球KdV方程。文献[2]导出了柱/球KdV方程，并利用坐标转换将柱KdV方程转化为普通KdV方程,得到了单孤波解，但没有得到球KdV方程的解析解。文献[3]利用齐次平衡原则得到了柱KdV方程的双孤波解。等离子体中的朗缪尔(Langmuir)孤波受到强烈的朗道(Landau)阻尼作用后将衰减,而孤立子的形成、发展和衰减的过程，反映了等离子体中波和粒子能量的转换作用,但一般认为衰减形式的孤立子无法给出解析表达式[4]。

衰减型孤波解是一个重要的研究领域,相关问题的研究将推进离子声波，特别是离子声孤波理论的进展。文献[5]借助Backlund变换和Hirota方法获得了柱KP方程的衰减型解。文献[6]借助简化齐次平衡原则得到非线性变换，得到了柱KP方程的衰减孤波解,参数取特殊值时，可以获得柱KdV方程的衰减型孤波解。但利用文献[6]的方法无法获得球KdV方程

的解析解。文献[7]无法给出上述球KdV方程的精确解，只给出了球KdV方程的近似解析解，并借助数值模拟来进行比较。文献[8]提出了一种求解球KdV方程的解法，借助变量变换将球KdV方程转换为变系数KdV方程，由于文献[8]中方程(16)形式有误，因而事实上并未解决球KdV方程求精确解的问题。而变系数KdV方程

ut+α(t)uux+β(t)uxxx=0

关于方程系数解析求解的限制条件[8-9]是：

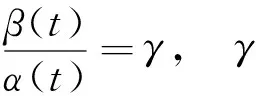
由此可以看出,变系数非线性数学物理方程要获得精确解析解，对方程的系数有一定的限定条件。文献[10]指出：对于南海北部孤立子内波的研究，可以通过参数调整来反演观测得到的孤立子内波,并据此探讨孤立子内波发生的动力机制和源地。可以考虑通过调整参数来获得球KdV方程的精确解析解。

本文考虑如下形式的球KdV方程：

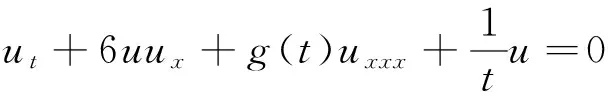
(1)

其中：g=g(t)作为色散项uxxx的系数，是可以调整的函数。下面将用简化齐次平衡原则[6,11-12]确定g=g(t)，并求出其精确解。

1 球KdV方程的非线性变换

考虑方程(1)中非线性项uux和色散项uxxx之间的齐次平衡[3,6,9,11-12](2m+1=m+3→m=2)，按照简化齐次平衡原则(用对数函数A(lnφ)取代HB方法中的F(φ))[6,11-12]，可设球KdV方程(1)的解具有如下形式：

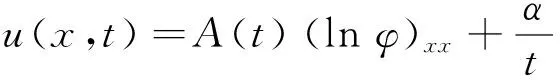
(2)

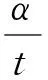
将式(2)代入方程(1)的左端得：

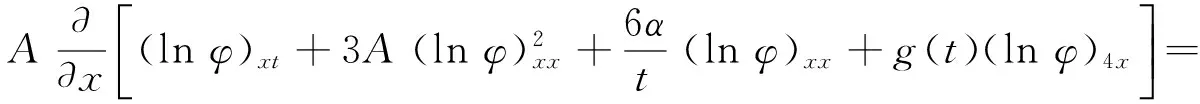
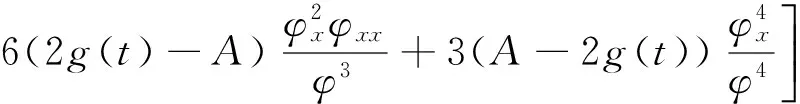
(3)

为了简化式(3),令A(t)与g(t)满足条件：

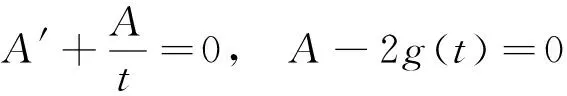
(4)

条件(4)有如下解：

(5)

其中：k为任意常数。

利用式(5),调整方程(1)中色散项的系数g(t)，则方程(1)成为如下形式的球KdV方程：

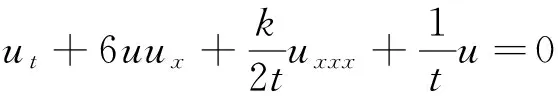
(6)

方程(6)的解具有如下形式：

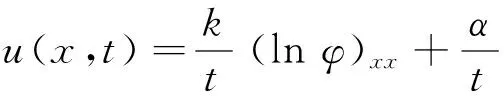
(7)

式(3)可简化为：

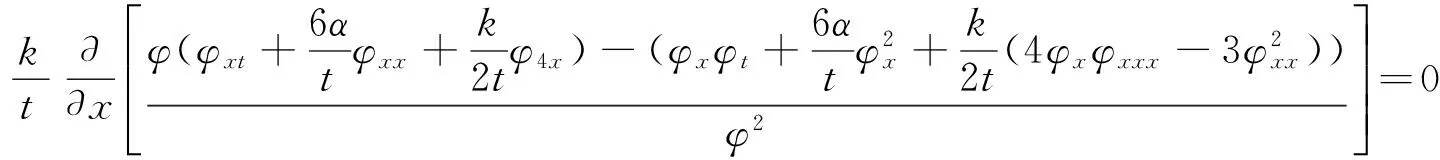
只要φ(x,t)满足齐二次方程

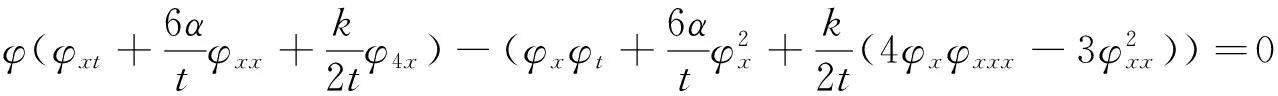
(8)

根据式(6)、式(7)和式(8)可得：若φ(x,t)是齐二次方程(8)的一个解，将其代入式(7)就得到球KdV方程(6)的解。式(7)和齐二次方程(8)就构成了球KdV方程(6)的一个非线性变换。

2 球KdV方程的精确衰减单孤波解

设齐二次方程(8)的一个解为：

φ(x,t)=1+eξ，ξ=λx+q(t)，

(9)

其中：λ为常数；q(t)为待定函数。

将式(9)代入齐二次方程(8)得：

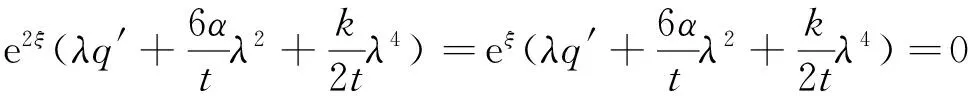
由方程

可解出:

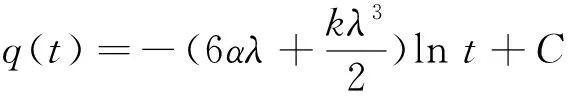
(10)

其中：λ,C为任意常数。将解(10)代入式(9)得齐二次方程(8)的一个解为：

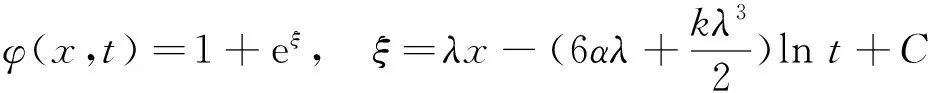
(11)

从而可得球KdV方程(6)的一个精确衰减单孤波解为：

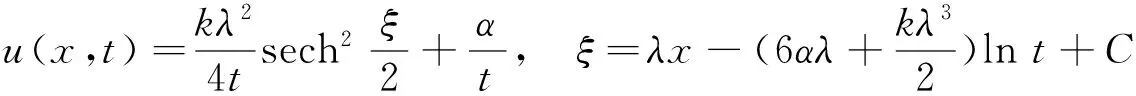
(12)

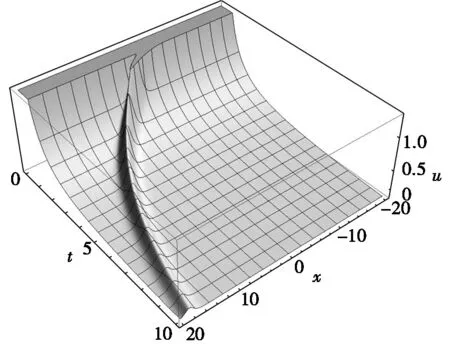
图1 k=1,λ=2,α=1时解(12)的图形

k=1,λ=2,α=1时，解(12)的图形见图1。从图1中可以看出：解(12)的振幅随时间t的增大而衰减。

3 球KdV方程的精确衰减双孤波解

为了获得球KdV方程(6)的更多解析解,需要找到齐二次方程(8)的更多解。设齐二次方程(8)的解具有如下形式：

φ(x,t)= 1+εφ(1)+ε2φ(2)+

ε3φ(3)+…，

(13)

其中：φ(i)(i=1,2,3,…)为待定函数；ε为小参数(为了简化可取ε=1)。将式(13)代入齐二次方程(8)，合并ε(i)(i=1,2,3,…)的同类项，令ε(i)(i=1,2,3,…)的系数为零，得到关于φ(i)(i=1,2,3,…)的一族方程为：

(14)

注意到方程族(14)的左侧均为线性方程,方程族(14)的第2式及以后的方程右侧依赖于前面方程解出的φ(i)(i=1,2,3,…),只要解出φ(1),便能依序从同样的线性方程中解出φ(i)(i=2,3,…)。由于方程族(14)的第1式为线性方程,φ(1)很容易解出。作为求解示例，取

(15)

易知，式(15)中的φ(1)满足方程族(14)的第1式。将式(15)代入方程族(14)的第2式右侧得：

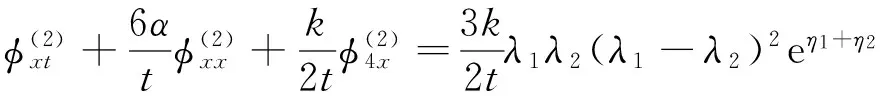
(16)

方程(16)有如下解：

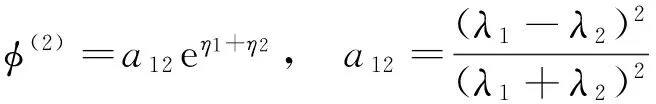
(17)

将式(15)、式(16)和式(17)代入方程族(14)的第3式，合并整理得：

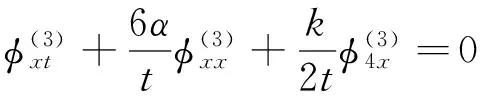
取φ(3)=0，从而

φ(n)=0，n≥3。

(18)

由式(18)可知，式(13)被截断。将式(15)、式(17)和式(18)代入式(13)，取ε=1，可得齐二次方程(8)的解：

φ(x,t)=1+eη1+eη2+a12eη1+η2。

(19)

将式(19)代入式(7)，得到球KdV方程(6)的精确衰减双孤波解：

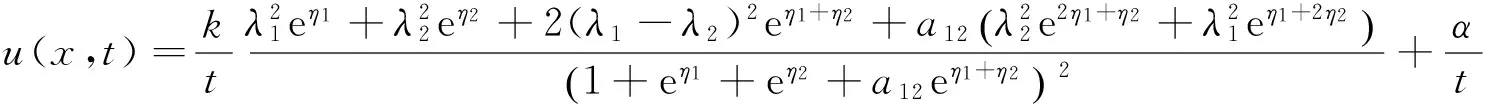
(20)

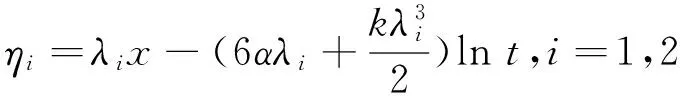
图2 k=1,α=1，λ1=2,λ2=3时解(20)的图形

4 结束语

对于通常的球KdV方程，至今尚无法求出其精确解。本文给出了一个变色散系数的球KdV方程，用简化齐次平衡方法求出了该球KdV方程的精确衰减单孤波解和双孤波解。

致谢:本文得到王明亮教授的指导，在此表示感谢。

[1] XUE J K.Cylindrical and spherical ion-acoustic solitary waves with dissipative effect[J].Physics letters a,2004,322:225-230.

[2] LIU H F,WANG S Q,WANG Z L,et al.Propagation of cylindrical and spherical dust-ion acoustic solitary waves in a relativistic dusty plasma[J].Advances in space research,2013,51:2368-2373.

[3] WANG M L,WANG Y M,ZHOU Y B.An auto-Backlund transformation and exact solutions to a generalized KdV equation with variable coefficients and their applications[J].Physics letters a,2002,303:45-51.

[4] 戴文龙,贺贤土,霍裕平,等.等离子体中Langmuir波、横波和离子声波相互作用过程的孤立子行为[J].物理学报,1987,36(1):67-73.

[5]DENGSF.ThedecaymodesolutionsforthecylindricalKPequation[J].Appliedmathematicsandcomputation,2012,218:5974-5981.

[6]WANGML,ZHANGJL,LIXZ.DecaymodesolutionstocylindricalKPequation[J].Appliedmathematicsandcomputation,2016,62:29-34.

[7] 石玉仁,杨红娟,段文山,等.柱Burgers方程和球Burgers方程的解析解[J].西北师范大学学报(自然科学版),2007,43(4):37-40.

[8] 付遵涛,刘式达,刘式适,等.含变系数或强迫项的KdV方程的新解[J].应用数学和力学,2004,25(1):67-73.

[9]WANGML,WANGYM.AnewBacklundtransformationandmulti-solitonsolutionstotheKdVequationwithgeneralvariablecoefficients[J].Physicslettersa,2001,287:211-216.

[10] 蔡树群,甘子钧.南海北部孤立子内波的研究进展[J].地球科学进展,2001,16(2):215-219.

[11]WANGML,LIXZ.SimplifiedHomogeneousbalancemethodanditsapplicationstotheWhitham-Broer-Kaupmodelequations[J].Journalofappliedmathematicsandphysics,2014,2(8):823-827.

[12]WANGML,ZHANGJL,LIXZ.N-dimensionalauto-Backlundtransformationandexactsolutionston-dimensionalBurgerssystem[J].Appliedmathematicsletters,2017,63:46-52.

国家自然科学基金项目(11301153,11601225);河南科技大学校级科技创新平台建设项目(2015XPT001)

李向正(1972-),男,河南偃师人,副教授,博士,主要研究方向为非线性数学物理方程.

2017-03-15

1672-6871(2017)06-0070-04

10.15926/j.cnki.issn1672-6871.2017.06.014

O175.2

A