城市路网中大型桥隧拥堵传播脆弱性研究
童 瑶,陆 键,操志强,陆林军
(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240;2.同济大学 交通运输工程学院,上海 201804;3.上海市计量测试技术研究院,上海 200231)
城市路网中大型桥隧拥堵传播脆弱性研究
童 瑶1,陆 键2,操志强3,陆林军1
(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240;2.同济大学 交通运输工程学院,上海 201804;3.上海市计量测试技术研究院,上海 200231)
针对路网脆弱性问题复杂多变,至今没有统一评价指标的问题,应用拥堵传播理论和动态交通分配的思想评价紧急情况下的交通破坏程度,提出了基于交通状况和路网拓扑两个方面的脆弱性评价指标。以上海外环内的主干路网为研究范围,借助Gephi和TransCAD仿真软件对13条越江隧道和4条跨江桥梁进行脆弱性评价,验证了评价模型的可行性。研究结果显示:桥梁比隧道更为脆弱,内环之内桥隧的脆弱性明显比外围更严重。其中,卢浦大桥和南浦大桥的脆弱性指标最大,分别为10.68%和10.62%。桥梁及隧道的位置和车道数在网络脆弱性中起着重要的作用。
网络脆弱性;拥堵传播;动态交通分配;大型桥隧
0 引言
随着上海城市化步伐的进一步加快,上海市人口和汽车数量急剧增加,给上海市路网的整体运营安全带来了极大风险。目前,上海市大量路段已饱和,路网吸纳新增交通量的能力越来越低,使得拥堵时间加长、拥堵面积扩大,早晚上班高峰时段主干路网的拥堵尤为严重;同时,主干路网的运营还受到很多潜在风险的影响。交通拥堵、交通污染和交通事故等交通问题已成为严重制约上海市发展的瓶颈。作为城市交通运营的主要载体,上海市主要路网的风险水平与日俱增。
大型越江桥梁隧道大多属于高速公路、快速路等级,车道数均为双向四车道及以上,具有降低环境污染、减少油耗、缩短出行时间、打通交通路网等功能。但是,遇到灾害天气时,大型桥隧不仅不能发挥其功能,还会造成交通拥堵和交通事故,成为路网中的瓶颈路段。本文选择上海市的13条越江隧道以及4条跨江大桥为主要研究对象,探究其脆弱性,以便深入研究主干路运营风险分布特征并揭示分布规律,有助于提高整个路网的安全水平,改善路网安全状况,提高整个上海市的道路网络运行效率。
关于网络脆弱性研究,国外学者主要关注理论研究,而国内学者更侧重理论与案例研究相结合。文献[1]阐释了路网脆弱性的定义,认为交通网络脆弱性是一个易受事件影响而导致路网服务水平极度下降的敏感系数。对脆弱性的描述可分为3大类:第1类将脆弱性理解为网络中部分失效造成的后果,例如,文献[2]认为脆弱性与灾害后果密切相关,即小部分路段失效将造成网络节点间可达性的显著降低,可达性指标就是节点脆弱性的表征;第2类认为路网脆弱性还与风险有关,既要考虑失效后果,也应考虑失效概率,例如,文献[3]认为脆弱性由发生危险事件的概率和在特定地点发生事件的后果两部分组成;第3类认为网络脆弱性不仅与网络结构有关,网络运行交通量、环境因素相关的属性也起着很大的作用[4]。本文更同意第3类意见,即脆弱性由网络结构和运行环境两部分组成。本文采用文献[5]中轮流断裂道路网的主要部分的方法,根据路网服务能力下降的影响确定具有较大脆弱性的断面。
复杂网络理论是脆弱性研究的重要基础之一。复杂网络理论提出了很多基于复杂网络拓扑结构的网络脆弱性指标,包括网络平均度、平均路径长度、聚类系数、介数和网络全局效率等。网络平均度可反映网络中节点之间连边的平均疏密程度;平均路径长度是所有节点对之间距离的平均值,是考量道路网络系统连通性及出行便利性的一个指标;聚类系数是表示一个图形中节点聚集程度的系数;介数指网络中所有经过该节点(边)的最短路径的数量比例,是发现和保护网络关键节点(边)的重要指标;网络全局效率表示去除某些节点之后的复合网络的有效性。各指标的具体计算公式见文献[6]。
文献[7]和文献[8]分别从两种攻击模式,即从随机攻击和故意攻击的网络拓扑角度研究了路网的脆弱性。文献[9]使用旅行分布数据分析了西班牙马德里地铁网络的脆弱性。文献[10]使用旅行成本增长参数作为度量指标。文献[11]则引入了行程时间评价因素。综上所述,大多数学者对脆弱性指标的选择不全面,所提出的算法只在小范围内被验证,没有在城市范围内推广,因此需要验证其实用性。本文将综合考虑交通状况和道路拓扑结构两种因素,运用文献[12]中动态交通分配理论的思想,提出更全面的脆弱性评估模型来评价路网中桥隧的脆弱性。
1 基于拥堵传播理论的路网失效模型
大型异常事件下,整个道路网络由于恶劣天气等的影响,整体通行能力水平一直较低。随着时间推移,这种拥堵状态会蔓延到临近的路段和交叉口,甚至会造成局部路网的交通拥堵。因此,不仅应考虑交通拥堵效应,还需进一步考虑拥挤的传播。本文应用级联失效模型进行模拟分析,研究道路拥挤效应的传播过程。该模型中,交通网络的节点和边只有正常和失效两种状态。道路的运行状态只与两个随机变量有关,即道路通行能力C和需求流量V。用Z表示道路运行功能,则Z=C-V。由于道路运行的不稳定性,当道路单元运行功能小于0时,可视为失效。因此,道路单元是否可靠,可通过以下3种情况进行描述:

(1)
假设道路网络G=(V,E)。根据级联失效模型,当节点和边上的负载超过其容量时,此路段由于交通拥堵将处于“失效状态”,与周边道路的交通联系也随之断开。在模型演绎中,应从网络中将该路段以及该路段与周边道路的连接删除,并对整个路网进行下一次的流量分配。借鉴这种理论,本文基于收敛的条件对交通拥堵在网络中的传播现象进行仿真,只要网络中存在失效路段,则根据模型对路网进行下一次交通分配,直至路网中不存在失效路段。通过对最终平衡状态网络结构性指标的计算,衡量网络的破坏程度。
2 越江桥隧脆弱性分析指标
大型桥隧不是网络拓扑结构相关指标最敏感的部分,但是由于其特殊的地理位置、自身结构缺陷和受环境扰动性,大型桥隧的失效会对整个网络运行带来毁灭性的破坏。同时,大型桥隧大多属于城市主干路网中的高速路或快速路,高峰时段交通量巨大。因此,需要结合拥堵脆弱性和路网拓扑结构脆弱性两方面评价桥隧整体脆弱性。
2.1 拥堵脆弱性指标
大多数文献选择交通量作为交通网络条件的评价指标,而忽略了道路通行能力的差异。文献[13]指出,V/C是指交通量和容量的比值,是一个无量纲的量,可以直接评价基于交通拥堵的设施服务能力。因此,V/C广泛用于交通系统评估,并能间接反映道路的服务水平。本文选择高峰时段道路的V/C来评估整个网络的运行状况,并使用TransCAD仿真软件实现整个网络的交通分配,以便从道路拥挤的角度评估网络的脆弱性。
交通拥堵指数(traffic congestion index,TCI)指的是对特定时刻单个道路路段或路网的拥堵强度进行量化后的相对值,体现单个路段或整个路网的拥堵强度和运行状态,是一个反映运行质量的无量纲量。交通拥堵指数是一个取值为0~5的连续变量,值越大表示道路运行状态越差,拥堵程度越严重;相反,值越小则表示道路运行状态越好,拥堵程度越轻。本文对TCI进行离散化处理,将路段交通拥堵指数、拥堵状况和V/C三者联系起来。相关道路拥堵指标参数如表1所示。为了便于计算,可建立网络拥堵性能(traffic congestion performance,TCP)指标,其计算公式如下:

表1 相关道路拥堵指标参数表

(2)
其中:i和j分别为路段的起始点节点;TCIij为路段ij的交通拥堵指数;Vij为通过路段ij的服务交通量;Cij为路段ij的道路通行能力。
2.2 路网拓扑结构脆弱性指标
一个客观全面的桥隧脆弱性总评价指标应该是既考虑了道路的拥堵运行状况,又要结合路网拓扑结构的特性。各指标的量纲不一样,为了统一比较,综合权衡各指标的权重,对所有指标采取归一化处理,运用失效前后的变化率将其归一化,具体计算公式如下:

(3)

为了更全面地衡量整个网络的拓扑结构,建议尽可能多地囊括网络拓扑结构的多个参数。度值、介数、平均路径长度从不同的方面反映出了网络拓扑结构脆弱性,三者对脆弱性的贡献度类似。整个路网拓扑结构脆弱性指标(topology vulnerability index,TVI)计算公式如下:
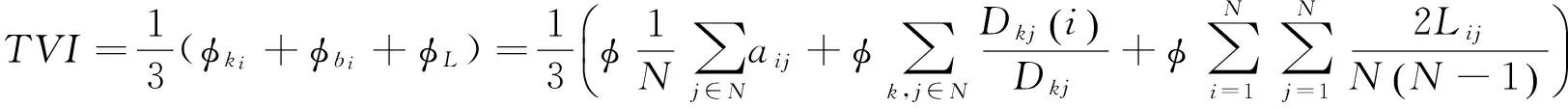
(4)
其中:ki为节点i的度;bi为节点i的介数;L为网络平均路径长度;N为网络中的节点数;i和j分别为路段的起始点节点;aij为邻接矩阵中对应值;Dkj(i)为经过节点i的最短路径数;Dkj为节点k和j的最短路径数;Lij为两个节点间的最短路径长度。
2.3 桥隧整体脆弱性评价指标
结合网络运行状况和拓扑结构,常用的网络脆弱性公式为wa=λ1×qa+λ2×Ca,其中:wa为道路a的整体脆弱性;λ1和λ2分别为交通运行状况指标qa和网络结构指标Ca的权重。选取网络拥堵性能指标TCP作为交通运行指标,选取路网拓扑结构脆弱性指标TVI作为网络结构指标,最终得到整体脆弱性评价公式:
Wa=λ1×φTCP+λ2×φTVI。
(5)
因为网络运行指标所占权重较大,取网络运行指标的权重为0.6,拓扑结构指标的权重为0.4,计算其脆弱性。结合式(3)将上述所有提及的运算指标无量纲化,得到最终结果。综上所述,路网中桥隧脆弱性的计算公式如下:
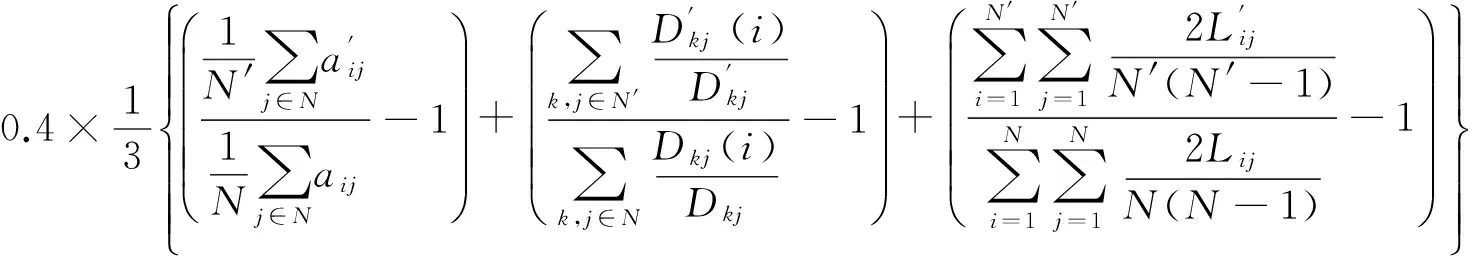
(6)
其中:W代表桥隧脆弱性;分母表示当某条桥隧失效时,整个道路网络经过动态交通分配后获得的拓扑结构参数以及网络拥堵评估系数;分子表示相应参数的原始状态。
3 案例分析
3.1 基础数据及拓扑建模
本案例的基础数据来源于上海市路政局的官方统计,主要包括2014年上海市主城区高速公路主要断面平均流量、快速路主要断面平均流量以及市域内大型桥隧机动车年平均日交通量。其中,高速公路和快速路的主要断面位置是指该路段标志性断面(如与其他路段的大型交叉口处),流量数据也是分双向统计的,流量单位为折合小客车当量(passengers car unit,PCU)。TransCAD软件的交通规划模块主要用于交通分配和拥堵分析[14],当输入所有路段信息和OD生成数据时,软件将计算所有路段的V/C。作为专门分析网络拓扑的常用工具,Gephi软件专门评估网络结构,计算复杂的网络理论指标,如网络中节点的度、中心性、接近中心性以及介数。
对上海市主要道路网络的拓扑结构进行抽象建模,将网络中的道路交叉口抽象为网络中的节点,交叉口间的路段映射为两节点的边,其中边是有向的,且大多为双向(包括外环内的13条大型越江隧道以及4条跨江大桥,它们是路网中关键研究路段)。随后,借助网络分析软件Gephi建立上海市主要道路网的拓扑模型,如图1所示,并评估其中大型桥梁和隧道的脆弱性。对于不同的网络特性,排名前5的节点分别在图中用不同的形状标记(包括并列第5),五边形标出的为介数排名前5的节点,三角形则表示度,菱形表示特征向量中心度,五角星表示接近中心性。图1直观地展示了初始状态下各个节点在拓扑网络中的脆弱性情况,被标记的形状越多,表示节点越脆弱。下文的网络结构指标计算中,均使用整个网络的平均值来衡量网络结构的脆弱性程度,即平均度、平均介数等。

图1 Gephi软件建立的上海市主要道路网拓扑模型
3.2 基于拥堵理论的路网动态交通分配
在TransCAD软件中建立整个上海市主干路网模型,包含关键的大型桥隧,并录入相应的路段信息和流量信息。基于上海市行政分区和具体地理位置划分交通小区,并根据路段截面流量信息进行交通反推,得到产生吸引点矩阵。之后的交通分配均采用此出行矩阵进行分配。
为研究大型桥隧各自的脆弱性,依次断裂每一条桥梁隧道及与其相连的道路,重新进行交通分配,每次交通分配均使用更为贴近实际的随机用户平衡模型。并根据提出的交通拥堵传播理论,每次分配后删除路网中失效桥隧周边新增的V/C超过1的路段,并重新迭代分配,直到不出现失效路段为止。
3.3 上海市大型桥隧脆弱性分析
根据式(6)提出的整体脆弱性评价指标公式,计算每条桥隧交通分配迭代最终的拥堵状况及有效道路网络拓扑结构参数(借助Gephi软件和TransCAD软件),得到整体脆弱性指标,上海市大型桥隧脆弱性分析结果统计表见表2。表2中,不同失效情况下动态流量所经历的具体分配次数显示在“总分配次数”列中,“排名”列中脆弱性指标从高到低排列。

表2 上海市大型桥隧脆弱性分析结果统计表
根据表2的评估结果,失效后大多数桥梁和隧道需经过10次以上的重新分配,才能消除其引起的拥堵的影响。在外环内的桥隧中,桥梁的脆弱性相对较高,这可能与它们的位置和交通量密切相关。根据V越大,脆弱性越大的原则,卢浦大桥以10.68%的脆弱性指标排名第一,显示卢浦大桥断裂对整个路网造成了极大的破坏。南浦大桥和徐浦大桥在道路网络脆弱性方面也起到重要作用,脆弱性指标分别为 10.62%和9.07%。而越江隧道中,外滩隧道、复兴东路隧道、翔殷路隧道、打浦路隧道等存在高度脆弱性,这表明内环位置更容易影响路网性能,应该加以关注。此评价结果与实际道路拥堵情况高度一致。如果可能,增加车道数量和及时的分流是必要的。
4 结束语
(1)不同桥隧的脆弱性评价结果差异明显,表明提出的评价指标适合于评价桥隧脆弱性,并且拓扑结构和交通量对于脆弱性有显著的贡献。
(2)大型桥梁的脆弱性明显高于隧道,这是因为桥梁车道数更多,道路等级更高,网路拓扑结构更为单一,并且相比于隧道车速限制较少。
(3)脆弱性高的桥隧需要进行更多次数的交通分配来达到最后的平衡状态,这是因为其具有显著的连接功能。脆弱性高的桥隧所处路网密度高,使得交通拥堵传播效应显著,失效反应影响广泛。
本研究在前人交通安全评估体系的基础上,融入了交通运行状态(V/C)的标准,提出了城市路网中大型桥隧拥堵传播脆弱性评价方法。评价指标全面,评价方法简单,可操作,且用动态迭代分配的方法保证了结果的可靠性,因此,值得在实际应用中进一步推广。然而,本文案例中运用到的数据是上海市路政局提供的年平均日交通量以及高峰小时平均交通量,虽然全面但是并不能体现交通需求的动态变化性和实时性,不便于深入研究路网脆弱性的变化、探索脆弱性随时空转变的过程。下一步将在上海市大型桥隧优化和建设中,研究如何强化网络中的脆弱部分,将脆弱性研究应用于实践,从而提高路网稳健性,更好地服务于乘客出行和城市发展。
[1] 杨露萍,钱大琳.道路交通网络脆弱性研究[J].交通运输系统工程与信息,2012,12(1):105-110.
[2] 徐秀珍,曾旗.物流运输网络连通可靠性分析的高效分解算法[J].计算机工程与应用,2016,52(17):24-28.
[3] 宋守信,许葭,陈明利,等.脆弱性特征要素递次演化分析与评价方法研究[J].北京交通大学学报(社会科学版),2017,16(2):57-65.
[4] 蒋海兵,张文忠,祁毅,等.高速铁路与出行成本影响下的全国陆路可达性分析[J].地理研究,2015,34(6):1015-1028.
[5] 吴贤国,黄艳华,刘惠涛,等.基于复杂网络理论的地铁线网脆弱性分析[J].重庆交通大学学报(自然科学版),2016,35(4):93-99.
[6] 田庆飞.基于复杂网络理论的城市公交网络生成与优化研究[D].长春:吉林大学,2013.
[7] 赵国锋,苑少伟,慈玉生.城市路网的复杂网络特性和鲁棒性研究[J].公路交通科技,2016,33(1):119-124.
[8] 孙建,胡志华.全球集装箱海运航线网络关键港口识别[J].河南科技大学学报(自然科学版),2016,37(6):95-99.
[10] 叶青,彭其渊.考虑客流拥堵的城轨网络脆弱性评估[J].计算机应用研究,2016,33(10):2923-2925.
[11] 关士托,孙健,徐婷.城市地铁开通对通勤者出行方式选择的影响[J].河南科技大学学报(自然科学版),2015,36(4):42-46.
[12] CANTARELLA G E,WATLING D P.A general stochastic process for day-to-day dynamic traffic assignment:formulation,asymptotic behaviour,and stability analysis[J].Transportation research part b(methodological),2016,92:3-21.
[13] 马聪,张生瑞,王晋.基于V/C比的公路养护施工区交通延误研究[J].公路交通科技,2013,30(7):133-139.
[14] CACAJ P,LAPA K.Trip distribution and traffic assignment flow of roads network in urban area in Vlora,with TRANSCAD[J].Constanta maritime university annals,2014,21(1):197-202.
国家自然科学基金项目(51508325)
童瑶(1992-),女,江苏泰州人,硕士生;陆键(1957-),男,通信作者,美国佛罗里达州人,教授,博士,博士生导师,主要研究方向为交通安全、交通规划和智能交通.
2017-03-02
1672-6871(2017)06-0053-06
10.15926/j.cnki.issn1672-6871.2017.06.011
U491.5
A

