M矩阵Fan乘积行列式下界估计

仲从磊，李灵晓

(河南科技大学 数学与统计学院，河南 洛阳 471023)

M矩阵Fan乘积行列式下界估计

仲从磊，李灵晓

(河南科技大学 数学与统计学院，河南 洛阳 471023)

针对M矩阵Fan乘积行列式的计算问题，结合M矩阵Hadamard乘积行列式的估计式，给出了M矩阵Fan乘积行列式下界的几个估计。对这些结果进行了比较和推广，并给出了相应的算例。研究结果表明：采用矩阵的顺序主子式替代矩阵元素后行列式多一正项，下界变大，结论更精确，有利于M矩阵Fan乘积行列式的计算。

M矩阵;Hadamard乘积;Fan 乘积;行列式;下界

0 引言

矩阵的Fan乘积是一种特殊的矩阵乘积，广泛应用于特征函数以及偏微分方程[1-4]的弱极小原理等方面的研究中。M矩阵是计算数学中重要的特殊矩阵类[5]，有着广泛的应用。生物、物理和社会科学中的诸多问题都与M矩阵有着密不可分的联系。因此，M矩阵Fan乘积行列式的计算和估计[6]成为特殊矩阵论研究的主要内容之一。其中，关于M矩阵Fan乘积行列式下界的估计是近几年的研究热点，并得到了一系列结论。但这些结论中的估计式需要借助于矩阵的所有元素进行计算，所需计算量较大且所得下界的误差较大。

本文结合M矩阵Hadamard乘积行列式的估计给出M矩阵Fan乘积的一些估计式，并对这些估计式做了比较。对于M矩阵Fan乘积的计算和特征值界的估计问题[6-7]，以及相关的偏微分方程数值解等有一定参考价值。

1 矩阵Fan 乘积定义

设Rm×n为全体m×n实矩阵的集合，矩阵A=(aij)∈Rm×n，矩阵B=(bij)∈Rm×n,其Hadamard乘积定义为一个m×n矩阵A°B，其中(A°B)ij=aijbij。A和B的Fan乘积定义为一个m×n矩阵A*B，其中：

如果aij≥bij对所有的i,j成立，则称A≥B。矩阵A∈Rn×n，如果A=sI-B且s>0,B≥0，s>ρ(B),其中,s为某一实数，I为n阶单位矩阵，ρ(B)为B的谱半径；称A为非奇异M矩阵，记Mn为全体n×n非奇异M矩阵的集合。 矩阵A∈Rn×n的比较矩阵定义为一个n×n矩阵μ(A)=(mij)，其中:

矩阵A∈Rn×n的全体k×k顺序主子矩阵记为Ak。

文献[6-10]给出了一些关于两个M矩阵Hadamard乘积行列式下界的估计不等式，经典的结果是：

定理1[6]若A=(aij)∈Mn,B=(bij)∈Mn,则

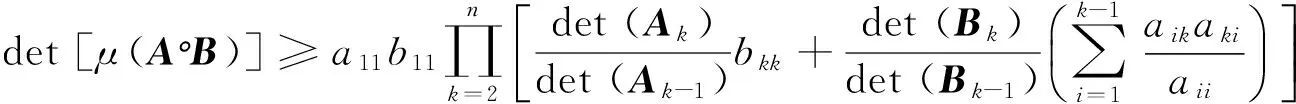
(1)

本文将上述结论推广到两个M矩阵Fan乘积上,并利用文献[5]的相关结论对其改进。

2 几个引理

引理1[9]如果A∈Mn,那么Ak∈Mk。

引理2[9]如果A=(aij)∈Mn,那么

det (Ak)≥0,k=1,…,n。

(2)

引理3[10]如果A∈Mn，B∈Mn，那么

(3)

证明 根据引理1,

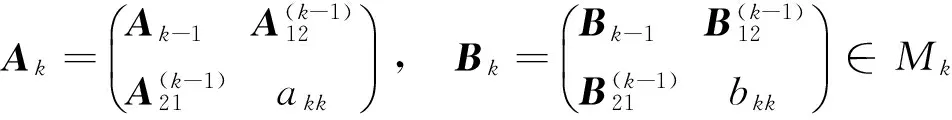
因此,

diag(a11,a22,…,ak-1,k-1)≥Ak-1；

并且

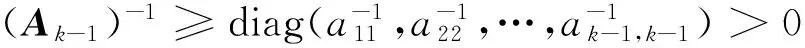
从而,

冲砂系统的开挖与常规的地下隧洞开挖有区别的，坡积体段管棚灌浆处理形成了封闭裂隙，加强基岩的完整性，达到提高岩体强度和刚度的。在开挖过程中明显出现砂砾石形成整体现象，加上临时支护及时，未出现大量塌方现象，说明该隧洞的坡积体段施工方法可靠。

(4)

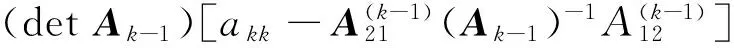
(5)

由式(2)、式(4)和式(5),可得：

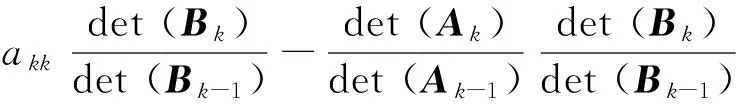
引理4[10]若A=(aij)∈Mn,B=(bij)∈Mn,则

3 主要结论

本部分将给出两个M矩阵A和B的det(A*B)界的估计不等式。

定理2 设A=(aij)∈Mn,B=(bij)∈Mn, 那么

A*B=μ(A°B)。

证明 因为A∈Mn、B∈Mn,易知aii>0,bii>0且aij≤0,bij≤0(i≠j)，从而

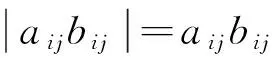
故

A*B=μ(A°B)。

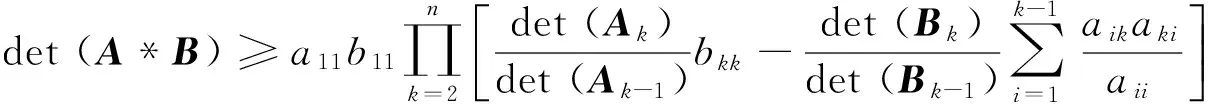
根据定理2和式(1)可得：

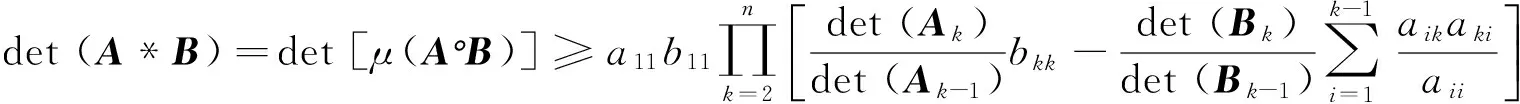
定理4 设A=(aij)∈Mn、B=(bij)∈Mn,那么

证明 由引理4可得：

根据引理3和定理2,易得：

det (A*B) =det [μ(A°B)] ≥

以上结论通过算例加以验证。

算例：

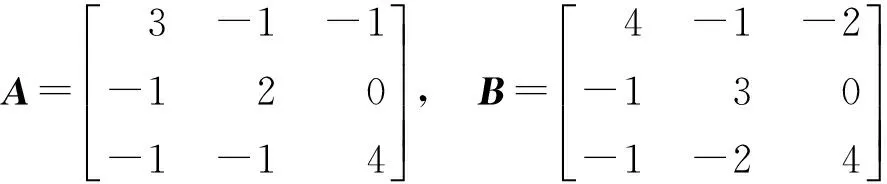
易知A和B都是M矩阵，且

det(A*B)=1 120；

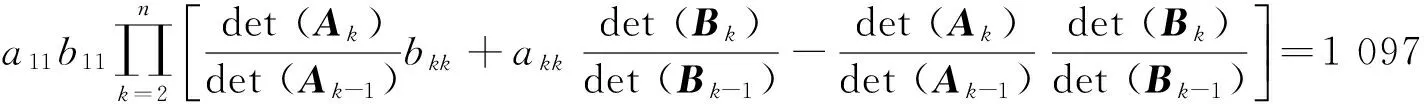
显然

det (A*B)= det [μ(A°B) ] ≥

上述算例表明定理4的结论比定理3的结论更加精确。

需要注意的是，矩阵的阶数每提高一阶，行列式的顺序余子式的个数会增加一个，估计算法计算量也会相应地增加，这个问题可以借助于计算机得到快速解决。对于偏微分方程数值解等问题中产生的稀疏矩阵，如果满足M矩阵的条件，尤其是对角占优矩阵，本文中的估计不等式也是成立的。文中的推导方法依据M矩阵Hadamard 乘积行列式的相关结论得出，今后也会有更加精确的估计式产生，同时也可以把相关的结论推广到两个H矩阵[11]的Fan乘积问题上。

[1] 王天军,殷政伟.Legendre-Gauss-Lobatto节点的一个注记[J].河南科技大学学报(自然科学版),2012,33(1):71-74.

[2] 王天军,贾丽蕊.非线性热传导方程的 Lagrange 插值逼近[J].河南科技大学学报(自然科学版),2011,32(2):67-71.

[3] 王天军,李清,殷艳红.非线性热传导方程混合问题插值逼近[J].航空计算技术，2012,42(2):1-3，12.

[4] 陶冬亚,焦琳,王天军.非线性Klein-Gordon方程的广义Hermite谱方法[J].河南科技大学学报(自然科学版),2015,35(6):87-90.

[5] 黄廷祝，杨传胜.特殊矩阵分析及应用[M].北京：科学出版社，2009.

[6] 周平,李耀堂.非负矩阵Hadamard积和M矩阵Fan积的特征值界的估计[J].纯粹数学与应用数学,2012,28(6):826-833.

[7]王峰.非奇异M矩阵的逆矩阵和M矩阵的Hadamard积的最小特征值下界估计[J].应用数学,2013,26(2):341-345.

[8]周平,高美平,李艳艳.M矩阵Hadamard积的新估计[J]．河北北方学院学报(自然科学版),2016,32(1):1-7.

[9]LIU J Z,ZHU L.Some improvement of Oppenheim’s inequality forM-matrices[J].SIAM journal on matrix analysis and applications,1997,18(2):305-311.

[10] YANG Z P,LIU J Z.Some results on Oppenheim’s inequalities forM-matrices[J].SIAM journal on matrix analysis and applications,2000,21(3):904-912.

[11]LI Y T,ZHONG C L.Some estimations for determinant of the Hadamard product ofH-matrices[J].Journal of computational mathematics,2005,23:401-407.

国家自然科学基金项目(11301152)；河南省教育厅自然科学基金项目(13B110999)

仲从磊(1979-)，男，山东济宁人，助教，硕士，主要研究方向为数值代数与特殊矩阵论.

2017-01-06

1672-6871(2017)06-0082-04

10.15926/j.cnki.issn1672-6871.2017.06.016

O241.6

A