改进模糊C均值聚类法的车辆实际行驶工况构建

高建平，高小杰

(河南科技大学 车辆与交通工程学院，河南 洛阳 471003)

改进模糊C均值聚类法的车辆实际行驶工况构建

高建平，高小杰

(河南科技大学 车辆与交通工程学院，河南 洛阳 471003)

针对模糊C均值(FCM)聚类法的性能依赖于初始聚类中心、迭代容易陷入局部极值、不能确保FCM收敛于一个最优解的问题，利用多岛遗传算法(MIGA)与序列二次规划法(SQP)组合优化，对FCM聚类的初始聚类中心进行优化，从而使聚类结果更加接近最优聚类。采用主成分分析和改进的FCM聚类分析，将运动学片段的特征值进行降维和分类处理，构建出基于大样本、符合郑州市交通特征的行驶工况。与试验数据对比表明:所构建的乘用车行驶工况与试验数据特征参数平均相对误差仅为2.097%，速度-加速度联合分布差异(SAFDdiff)仅为1.74%，行驶工况拟合精度较高，更能综合反映郑州市交通真实状况。

FCM聚类；聚类中心；主成分分析；行驶工况

0 引言

能量消耗是衡量汽车产品质量性能的重要指标之一。汽车行驶工况是汽车能耗和排放测试方法的基础，是汽车各项性能指标标定优化时的主要基准。目前，被广泛使用的3大典型工况分别是：欧洲行驶工况(ECE15+EUDC)、美国行驶工况(FTP75)和日本行驶工况(JPAN10)[1]。

中国一些学者对行驶工况进行了深入研究，并取得了很多研究成果。文献[2]提出一种基于K-均值聚类算法的城市循环工况构建方法，拟合出某城市循环工况。文献[3]利用全球定位系统(global positioning system,GPS)设备对哈尔滨市主城区运行的乘用车工况数据进行了测试，构建了具有代表性的哈尔滨市主城区乘用车典型行驶工况。文献[4]利用组合聚类法及模糊C均值(fuzzy C-means,FCM)聚类法，对合肥市实际道路工况进行研究并建立合肥市区的典型行驶工况。文献[5]对天津市纯电动汽车道路行驶工况进行了研究，构建了适用于天津市的纯电动汽车行驶工况。文献[6]通过获取某型号公交车在济南市运行工况的实测数据，采用聚类加马尔可夫(Markov)链的方法构建了济南市公交车典型行驶工况。

主成分分析与聚类分析理论被广泛应用于车辆行驶工况的构建[7-10]。主成分分析主要是一种考察多个定量变量间的相关性的多元统计方法，可以进行降维处理，在主成分分析的基础上进行聚类分析，将不同行驶特性的短行程进行分类再抽取，从而构建代表性工况。聚类效果的好坏对最终拟合出的行驶工况的精度起着决定性的作用，例如FCM算法在给定聚类中心的情况下可以接近最优聚类[4]，但是单一的聚类方法存在一些缺陷。因此，本文利用多岛遗传算法(multi-island genetic algorithm,MIGA)与序列二次规划法(sequential quadratic programming,SQP)优化所得的聚类中心，作为FCM聚类的初始聚类中心，从而使聚类结果更加接近最优聚类，进而更加准确地构建出符合郑州市实际道路特点的车辆行驶工况。

1 工况构建的基本理论与数据处理

1.1 数据采集

目前，广泛应用的3大类车辆行驶数据的采集方法有：目标跟踪法、循环路线法和自主行驶法[9]。不同的采集方法会得到不同的采集数据，这将会直接影响车辆行驶工况构建的效果。由于自主行驶法是指驾驶员可以按照自己的方式驾驶汽车，更加符合人的驾驶习惯，使采集的数据能更加真实地反映交通状况，因此，本次数据采集试验采取自主行驶法。

本文主要采集车辆瞬时燃油消耗量、运行速度、GPS位置和车辆运行时间等参数。采样间隔对所采集到的数据质量有很大影响[9]。为了避免由于采样间隔设置不当，导致所采集的原始试验数据无法真实反映车辆的行驶状态，将选用的车载终端设备安装于试验车辆，行驶数据由车载终端设备实时采集，采样频率为1 Hz[9]。在正常工作状态下，车载终端与整车的电子控制单元(electronic control unit，ECU)进行通信，采集控制器局域网络(controller area network，CAN)总线的信息，获取车辆当前状态下的相关参数。车载终端设备通过外置的GPS天线接收时间、位置、车速等信息，通过通用分组无线服务(general packet radio service，GPRS)技术网络，将采集到的车辆运行过程中的相关信息传送给车辆远程管理服务平台，然后从中国汽车工况信息化系统查询并下载数据。

1.2 运动学片段划分及特征参数提取

图1 运动学片段定义示意图

对于一个运动学片段，无法用单一的特征参数(如速度)来进行全面系统地描述，想要完整地描述这个过程，还要用到其他参数，如平均速度及标准差、加速度及标准差、持续时间和怠速时间等。根据文献[2-8]，本文引入13个特征参数对运动学片段进行全面系统地描述:s为平均运行距离，m；Vavg为平均速度，m/s；Vmax为最大速度，m/s；Tall为运行时长，s；Till为怠速时间，s；Tacc为加速时间，s；Tdec为减速时间，s；Tcon为匀速时间，s；Amax为最大加速度，m/s2；Amin为最小加速度，m/s2；Aavg为加速段平均加速度，m/s2；Aavg-为减速段平均加速度，m/s2；PKE为正动能，m/s2。

利用MATLAB软件编写m文件，对采集的400多万组数据进行筛选预处理后，将其分成41 291个运动学片段，最终得到一个以样本数量(行)×特征参数(列)的矩阵，运动学片段特征参数如表1所示。

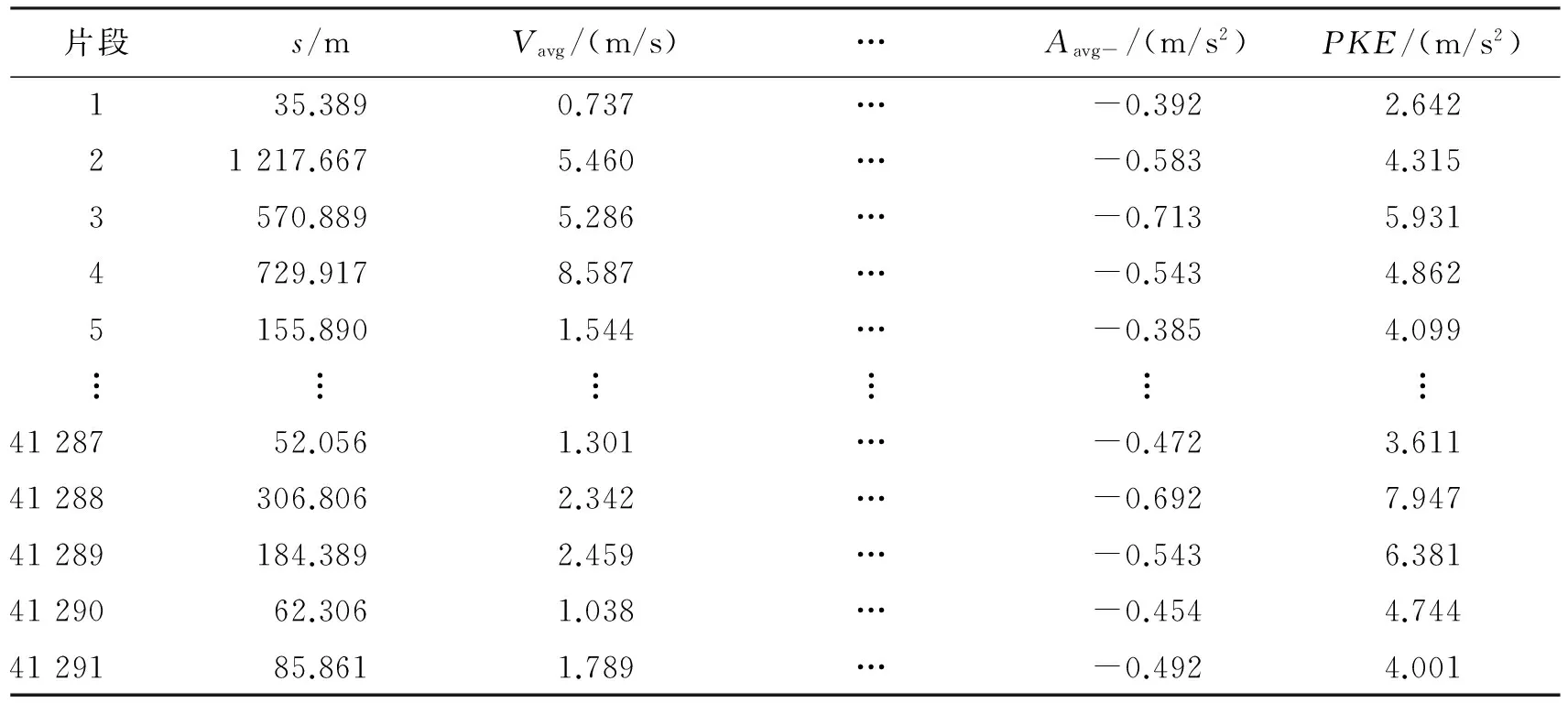
表1 运动学片段特征参数

1.3 运动学片段预处理

车辆在行驶过程中会产生一些突发行驶状况，数据采集过程中由于采集设备的信号问题，也会产生一些异常运动学片段不能代表当地交通特征的情况。以41 291个运动学片段的特征值为研究对象，剔除与当地车辆交通特点不符合的样本片段，使聚类效果真实地反映当地车辆实际的运行特点。通过对车辆用户进行问卷调查，得到采集设备车辆的实际行驶特点，去除片段中最大加速度大于3 m/s2、最大减速度大于 4 m/s2的运动学片段，最终得到35 506个有效运动学片段，占总样本数的85.99%。

1.4 主成分分析

在实际问题研究过程中，需要考虑更多的影响因素，从而更加全面系统地分析问题。对于问题的描述，每个变量都从不同的角度反映问题的一些信息，并且不同的变量之间也会有一定的关系。主成分分析可以通过消除变量之间的相关性，得到几个综合变量用来反映所研究问题的大部分信息，不仅可以反映事物的本质，而且简化了后续的计算。

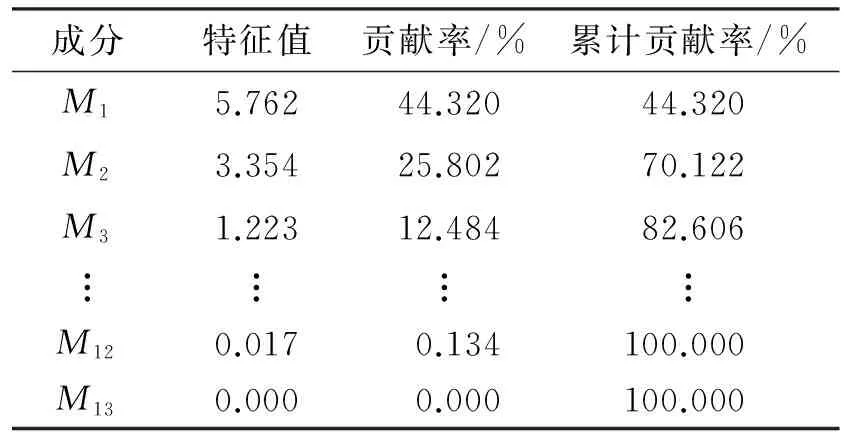
表2 各主成分贡献率及累计贡献率

利用MATLAB软件对运动学片段的特征值进行主成分分析，得到13个主成分，使用Mi(i=1,2,…,13)表示。各主成分贡献率及累计贡献率如表2所示。

由表2可知：前3个主成分的累计贡献率已经达到了82.606%，可以表征整个运动学片段的信息，而且前3个主成分的特征值都大于1，故选择前3个主成分用于聚类分析。

1.5 组合优化算法

数值型优化技术可以快速地找到局部最优点，但是不能很好地进行全局寻优;探索型优化技术可以找到全局最优点，但是后期效率较低，局部寻优不佳。因此，把这两种技术组合在一起构成组合优化技术，通过全局探索把最优点定位到局部区域，再通过数值型优化技术找到最优点，充分利用两种优化算法的优点[11-12]。

本文利用isight软件集成多岛遗传算法(MIGA)全局优化和序列二次规划法(SQP)局部优化进行组合优化设计[11]，对最终选取的用于聚类的样本数据的聚类中心进行优化处理，进而得到最好的聚类效果。优化的数学模型如式(1)所示，isight软件组合优化如图2所示。

(1)

根据道路交通特点，城市车辆运动学片段一般可分为城市闹市区、城市生活区和城市郊区3个类别。基于得到的3个主成分，利用组合优化算法将得到的35 506个运动学片段的初始聚类中心进行优化，得到优化后的3个类别的初始聚类中心分别为：C1=(3.600,-0.749,0.041)、C2=(-0.137，1.620，-0.002)、C3=(-1.500，-1.257，-0.017)。

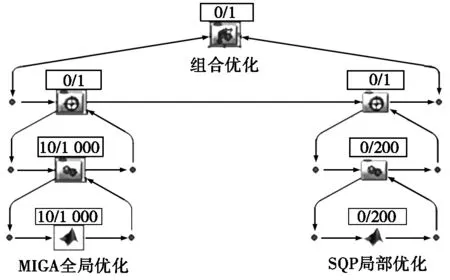
图2 isight软件组合优化图

1.6 FCM聚类算法

模糊聚类通过使用模糊理论对数据进行分析和划分，建立不确定性的样本类属描述，可以比较客观地反映事物本身的属性。模糊聚类就是让所属同一类别的所有样本数据相互之间的相似度最大，不同类别之间样本的相似度最小。

将优化后得到的3类初始聚类中心作为FCM的初始聚类中心，得到每个运动学片段所属类别以及3类行驶工况的最终聚类中心：C1=(2.708,-0.434,0.044)、C2=(-0.263，1.414，-0.047)、C3=(-1.642，-1.232，-0.108)。利用3个主成分表示改进FCM聚类后的结果，如图3所示。图3a为35 506个运动学片段以3个主成分聚类的三维散点图，从图3a中可以看出:3类行驶工况分类效果较好。图3b为35 506个运动学片段以前2个主成分聚类的散点图，从图3b中可以看出：所划分的3类工况聚类界限清晰，表明所提出的改进FCM聚类法聚类效果较好。

图3 改进FCM聚类结果图

表3为各类数据综合特征值。表3中：第1类代表车辆在城市郊区的模式；第2类代表车辆在城市生活区的模式；第3类代表车辆在城市闹市的模式；Pi为怠速比例，%；Pa为加速比例，%；Pd为减速比例，%；Pc为匀速比例，%。从表3可以看出：第1类平均运行时间为154.421 s，该类工况的匀速比例大，怠速比例小，且平均速度为23.947 km/h，说明该道路车流量较少、较畅通。第2类平均运行时间为72.777 s，由于道路车流量被限制，所以怠速比例较大，匀速比例较小，平均速度为15.959 km/h。第3类平均运行时间为41.395 s，说明该道路比较拥堵，车流被严重限制，运行速度较低，平均速度为7.398 km/h。

表3 各类数据综合特征值

1.7 代表性循环工况的合成

本文将车辆循环工况时间定为1 200 s左右[13]，通过计算聚类得到各类样本总时间占样本数据的总时间比例，由式(2)确定拟合出的最终循环工况中各类的时间长度。不同行驶工况的时间比例和时间长度如表4所示。

(2)

其中：ti为簇i在拟合工况中的持续时间，s；tdrivingcycle为最终代表性工况的持续时间,s；toverall为所有工况块数据的总持续时间,s；ti,j为簇i中工况块j的时间,s；nj为簇i中所有工况块的总数。

表4 不同行驶工况的时间比例和时间长度

计算各类样本中的各个片段与该类总样本数据的相关系数，并从中分别选取与该类所有数据相关系数大的运动学片段来表示城市闹市、城市生活区、城市郊区的车辆行驶工况特点。参考表4中不同的行驶工况所占的时间长度，为使选取的各类行驶工况总时间与其接近，最终选取5个城市郊区片段共533 s、6个城市生活区片段共370 s、6个城市闹市片段共312 s，因此，本文构建郑州市的循环工况时间长度为1 215 s。所构建的郑州市乘用车道路行驶工况如图4所示。

2 结果分析及验证

图4 改进FCM聚类法构建的郑州市乘用车道路行驶工况

2.1 基于特征参数的误差对比分析

本文选取8个特征参数为准则数，分别计算出拟合的1 215 s郑州循环工况与35 506 个有效运动学片段组成的样本试验数据的8个特征参数，道路试验总数据与所构建行驶工况的比较如表5所示。

由表5可知：改进FCM聚类法所拟合得到的郑州市道路行驶工况与试验数据特征参数的平均相对误差仅为2.097%，而改进前FCM聚类法所拟合得到的郑州市道路行驶工况与试验数据特征参数的平均相对误差为2.426%。从表5中改进前后FCM聚类法特征参数的相对误差对比可以看出：改进后的特征参数相对误差中，只有减速段平均加速度Aavg-与正动能PKE比改进前的大，其余特征参数相对误差均比改进前小。因此，改进FCM聚类法得到的郑州市代表性行驶工况在特征值方面精度更高、更合理，更能反映郑州市的实际道路交通状况。

表5 道路试验总数据与所构建行驶工况的比较

2.2 速度-加速度联合分布验证

从速度和加速度2个角度同时验证所构建行驶工况与原始试验数据之间的差异[13-14]，是比较严格的验证方法，因此，采用速度-加速度联合分布图来验证所构建的行驶工况，见图5。利用MATLAB软件分别计算试验数据与改进FCM聚类法构建的工况数据的速度-加速度联合分布矩阵，得到改进FCM聚类法构建工况的速度-加速度联合分布图，如图5a所示，试验数据速度-加速度联合分布图如图5b所示。对比图5a与图5b可以看出：速度-加速度联合概率分布整体趋势比较一致，且多位于速度为20～50 km/h，加速度较低区域。因此，改进FCM聚类法构建工况整体符合郑州市乘用车的行驶特点，能够满足开发需求。

图5 工况数据速度-加速度联合分布图

计算试验数据与改进FCM聚类法构建的行驶工况速度-加速度联合分布的概率误差，并作图，如图6所示。从图6可看出：联合分布概率误差最大绝对值没有超过15%，且联合分布概率误差大部分都在5%以内。速度-加速度联合分布差异计算公式[15]为：

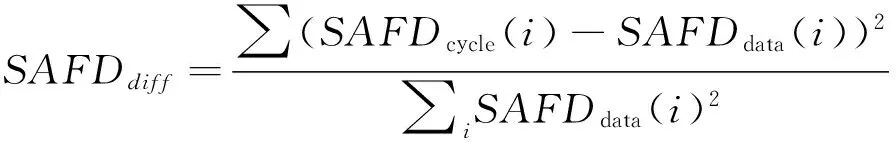
(3)

其中：SAFDdiff为速度-加速度联合分布差异；SAFDcycle(i)为代表性工况速度-加速度联合分布的第i个区间的值；SAFDdata(i)为采集试验数据所对应速度-加速度联合分布的第i个区间的值。

根据式(3)计算得出：试验数据与改进FCM聚类法构建的郑州市行驶工况数据的速度-加速度联合分布差异(SAFDdiff)为1.74%；试验数据与未改进聚类法构建的郑州市代表性行驶工况数据的SAFDdiff为2.65%。由此说明，改进FCM聚类法拟合得到的郑州市乘用车道路行驶工况更能综合表征郑州市乘用车交通的实际行驶特点。

图6 试验数据与改进FCM聚类法构建的行驶工况速度-加速度联合分布概率误差

3 结论

(1)利用多岛遗传算法与序列二次规划法的组合优化算法对FCM聚类的初始聚类中心进行优化，从而使聚类结果更加接近最优聚类。

(2)利用主成分分析法和聚类分析法对特征参数进行了降维和分类处理。利用相关系数提取了代表性行驶工况片段，进而构建出基于大数据的、更加符合郑州市交通特征、长度为1 215 s 的郑州市乘用车行驶工况。

(3)通过特征参数误差和速度-加速度联合概率分布误差分析，得到合成工况与试验数据特征参数平均相对误差仅为2.097%，合成工况与试验数据的速度-加速度联合分布差异(SAFDdiff)仅为1.74%，充分表明本文所用方法能够获得与实际工况更相近的典型行驶工况。

[1] 姜平,石琴,陈无畏.基于马尔科夫的城市道路行驶工况构建方法[J].农业机械学报,2009,40(11):26-30.

[2] 秦大同,詹森,漆正刚,等.基于K-均值聚类算法的行驶工况构建方法[J].吉林大学学报(工学版),2016,46(2):383-389.

[3] 郑殿宇,吴晓刚,陈汉,等.哈尔滨城区乘用车行驶工况的构建[J].公路交通科技,2017,34(4):101-107.

[4] 石琴,郑与波,姜平.基于运动学片段的城市道路行驶工况的研究[J].汽车工程,2011,33(3):256-261.

[5] 庄继晖,谢辉,严英.基于GPRS的电动汽车道路行驶工况自学习[J].天津大学学报,2010,43(4):283-286.

[6] 苗强,孙强,白书战,等.基于聚类和马尔可夫链的公交车典型行驶工况构建[J].中国公路学报,2016,29(11):161-169.

[7] 李孟良,朱西产,张建伟,等.典型城市车辆行驶工况构成的研究[J].汽车工程,2005,27(5):557-560.

[8] 胡志远,秦艳,谭丕强,等.基于大样本的上海市乘用车行驶工况构建[J].同济大学学报(自然科学版),2015,43(10):1523-1527.

[9] 李孟良,张富兴,李宏光,等.不同的采样间隔对车辆行驶工况测定影响的研究[J].汽车工程,2005,27(3):316-319.

[10] LIN J,NIEMEIER D A.An exploratory analysis com-paring a stochastic driving cycle to California’s regulatory cycle[J].Atmospheric enviroment,2002,36(38):5759-5770.

[11] 高建平,乔宏冰,郗建国,等.并联混合动力汽车传动系速比优化[J].河南科技大学学报(自然科学版),2014,35(6):25-29.

[12] 杨忠凯,廖连莹,左言言,等.混合动力汽车动力耦合行星齿轮系动力学模态[J].河南科技大学学报(自然科学版),2015,36(2):14-17.

[13] 姜平.城市混合道路行驶工况的构建研究[D].合肥:合肥工业大学,2011.

[14] ADAK P,SAHU R,ELUMALAI S P.Development of emission factors for motorcycles and shared auto-rickshaws using real-world driving cycle for a typical Indian city [J].Science of the total environment,2016,544:299-308.

[15] BRADY J,O’MAHON M.Development of a driving cycle to evaluate the energy economy of electric vehicles in urban areas[J].Applied energy,2016,177:165-178.

河南省科技攻关计划基金项目(152102210073);河南省高等学校青年骨干教师计划基金项目(2015GGJS-046)；河南科技大学第六届研究生创新基金项目(CXJJ-2016-ZR01)

高建平(1976-),男,河南洛阳人,副教授,博士,硕士生导师,主要从事新能源汽车方面的研究.

2017-04-14

1672-6871(2017)06-0021-07

10.15926/j.cnki.issn1672-6871.2017.06.005

U46

A