隧道开挖引起既有建筑物桩侧摩阻力的理论研究

田晓艳，李 源

(1.西安石油大学 机械工程学院，陕西 西安 710065；2.中国建筑西北设计研究院有限公司，陕西 西安 710018)

隧道开挖引起既有建筑物桩侧摩阻力的理论研究

田晓艳1，李 源2

(1.西安石油大学 机械工程学院，陕西 西安 710065；2.中国建筑西北设计研究院有限公司，陕西 西安 710018)

择优选取桩土荷载传递的侧摩阻力计算模式，借助文克尔地基模型，运用两阶段分析理论探究隧道开挖对桩基效应的影响。阶段1解出相应桩位处的沉降量并用多项式简化，阶段2将其沉降施加于桩侧建立桩身沉降微分方程。通过逻辑推导并借助边界条件得到沉降计算表达式，继而得到桩侧摩阻力和桩周轴力。结合工程算例，根据隧道与桩基的空间位置关系分析桩侧摩阻力和桩周轴力随桩长的变化规律。研究结果表明：对于给定的围岩土质概况，若保持桩隧距离不变时，桩长对桩基效应变化影响较大；桩长小于15 m时，土体位移稍大于桩位移，单桩沉降很大，且单桩主要承受负摩阻力效应；桩长超过15 m时，土体位移明显大于桩位移，部分桩段承受负摩阻力，部分桩段承受正摩阻力，且摩阻力为0处的单桩轴力最大。

荷载传递；两阶段分析；隧道开挖；桩身沉降微分方程；桩侧摩阻力

0 引言

桩侧摩阻力是桩土间相对位移产生的，其数值量化及曲线分布模式与深部土层变位有关，且曲线分布模式决定其轴力分布特点。若桩侧土体竖向位移大于桩基沉降时，土表现为对桩的下拽作用，即桩基产生负摩阻力；反之，土对桩有上撑作用，即产生正摩阻力。负摩阻力是个非常复杂的问题，一般易在软弱地层、湿陷性黄土区域、新近填土或欠固结土质出现。负摩阻力加大了桩基附加轴力，故而弱化桩基承载力，且工程上很多建筑物因其负摩阻力过大而不能正常使用，所以桩基负摩阻力受到国内外工程界相关人员关注。迄今为止，对竖向荷载下桩基侧摩阻力的探讨主要集中在室内试验[1-3]、理论分析[4]和有限元数值模拟[5-6]领域。

由于城市地面交通压力以及规划用地的紧张，地下工程必须修建于既有桩基附近，必然会扰动邻近围岩土层，继而破坏其初应力场，而土体变形会通过桩基与土体间相互作用传递到邻近桩基，导致桩基发生变形。目前，针对隧道开挖对桩侧摩阻力的分析主要在数值模拟[7-10]方面，且理论研究落后于实践，本文针对该问题进行理论探究，以期为类似工程提出一定的理论支撑。

1 基本微分方程的建立与求解

1.1 微分方程的建立

借助基本假定列出桩基沉降的微分方程：桩假定为文克尔(Winkler)弹性地基梁；桩土间不发生滑移，且相互作用采用连续分布的弹簧进行模拟。

图1为桩基计算简图。依据图1微分单元力的平衡条件建立方程：

N(z)+τ(z)updz-[N(z)+dN(z)]=0，

(1)

其中：N(z)为某深度z处桩轴力，kN;τ(z)为某深度z处侧摩阻力，kPa;up为桩截面周长，m。

式(1)化简得：

dN(z)/dz-τ(z)up=0。

(2)

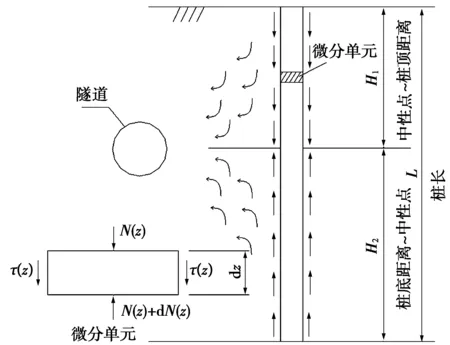
图1 桩基计算简图

由胡克(Hooke)定律得：

N(z)=-ApEpdw(z)/dz,

(3)

其中：Ep为桩身弹性模量，kPa；Ap为桩身横截面积，m2；w(z)为桩身竖向位移，m。

联立式(2)和式(3)得桩身竖向位移微分方程为：

EpApdw2(z)/dz2+upτ(z)=0。

(4)

1.2 荷载传递函数的侧摩阻力计算方法

常见的传递函数模型[11]有 Kezdi指数曲线、佐藤悟理想弹塑性曲线、Gvardner双曲线等，鉴于佐藤悟理想弹塑性曲线模型既考虑了桩土间的剪切位移以及桩土接触特征，并且在数学处理期间极为简洁，故选取模型：

(5)

其中：τ(z)为桩侧摩阻力，kPa;τmn、τms分别为桩侧摩阻力限值，kPa；s(z)、w(z)分别为土体沉降和桩身沉降，m；Smn、Sms分别为负、正摩阻力的剪切位移极限值，m；k为比例系数，黏性土k为4～6 mm，砂类土k为6～10 mm。

当桩土间无相对滑移时，文献[12]将桩周变形土体视作同心圆柱体，给出地下z处、距桩轴r处的桩侧土体变形与其摩阻力的关系：

u(z,r)=τ0r0ln (rm/r)/Gs，

(6)

其中：u(z,r)为地下z处、距桩轴r处的桩侧土体变形，m;Gs为剪切模量，kPa；rm为受荷桩对土体的最大影响半径，m；r0为桩径，m;τ0为摩阻力，kPa。

联立式(5)和式(6)得：

τ(z)=Gs[s(z)-w(z)]/[r0ln (rm/r0)]，

(7)

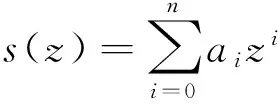
联立式(4)和式(7)得：

EpApdw2(z)/dz2+2πGs[w(z)-s(z)]/ln (rm/r0)=0，

(8)

其中：Ap为截面积，m2；Ep为弹模，kPa。

令kz=2πGs/ln (rm/r0)，则由式(8)可得：

dw2(z)/dz2=kz[w(z)-s(z)]/EpAp，

(9)

其中：kz为桩侧土竖向弹簧刚度，N/m。

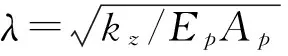
dw2(z)/dz2-λ2w(z)=-λ2s(z)。

(10)

1.3 桩身沉降求解

利用常数变易法求出方程(10)的解为：

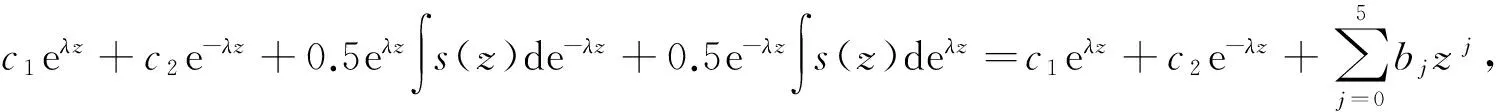
(11)

w*(z)是特解，且

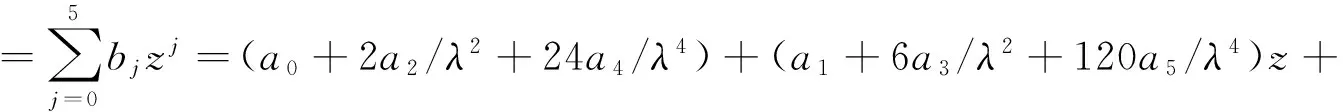
(12)

c1、c2通过下式来确定：

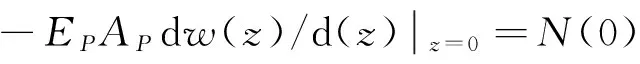
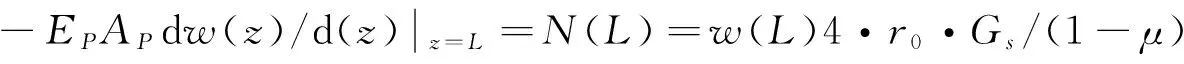
桩侧摩阻力：

(13)

附加轴力：

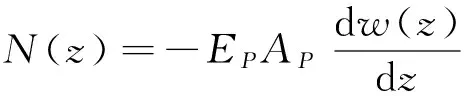
(14)

2 算例分析

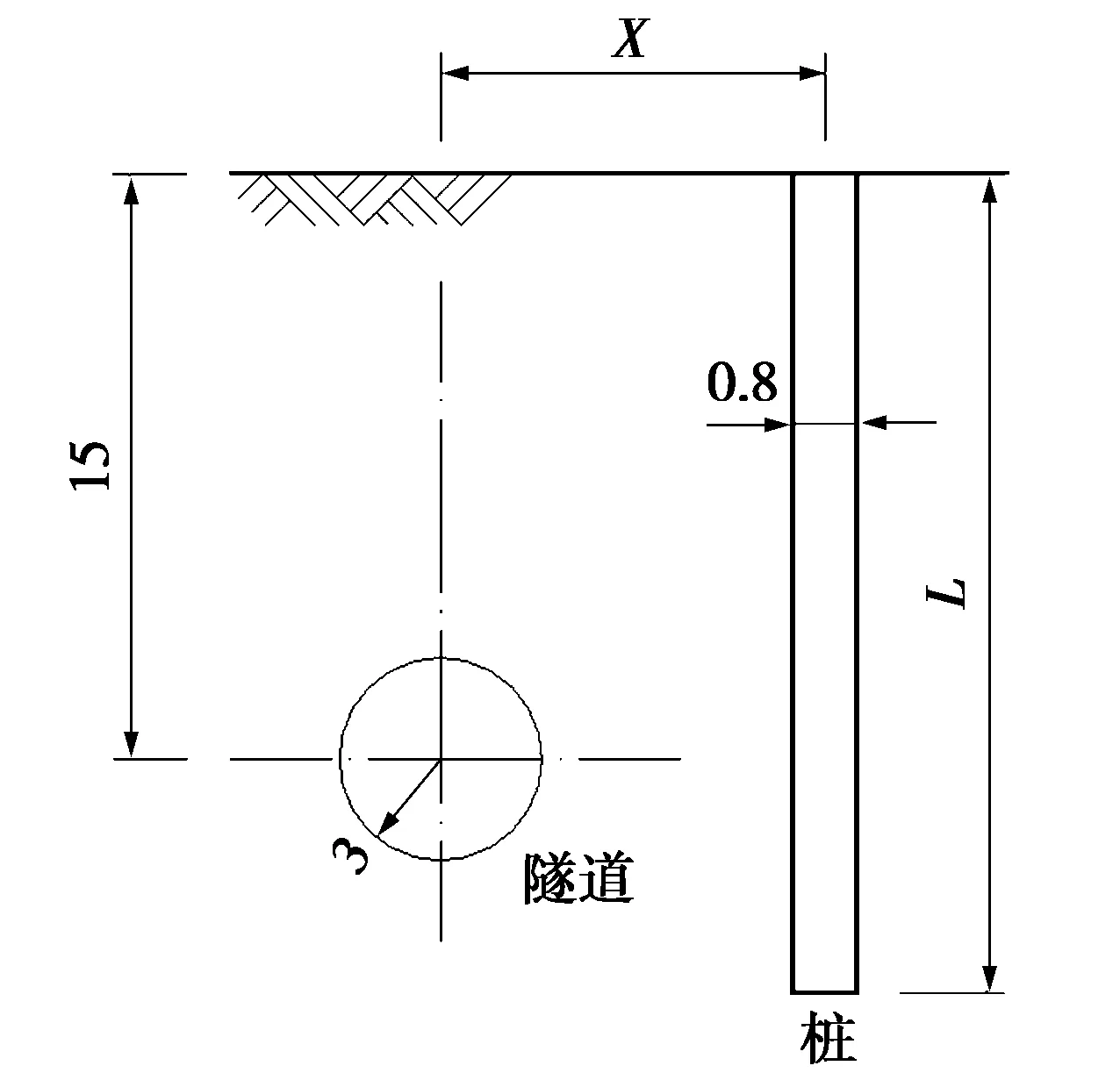
图2 隧道与单桩的计算简图(单位：m)

隧道与单桩的计算简图见图2。图2中：X为桩与隧道中心的距离，m;L为桩长，m。隧道参数：隧道半径R=3 m，隧道埋深H=15 m，地层损失比取2%；桩参数：C35混凝土，d=0.8 m。本文研究X=4 m时，分别对短桩(L=10 m)、中长桩(L=25 m)、长桩(L=45 m)效应的影响。

图3为X=4 m的土体位移及桩效应图。由图3a可知：当桩基距离隧洞边1 m(即桩隧轴线间距4 m)时，L=10 m，桩身均位于隧道分裂面之上，桩几乎随土层同步下沉，沉降量相对较大，为26.40 mm；L=25 m，部分桩身位于分裂面之上，沉降量减小，为15.25 mm；L=45 m，桩身大部分都处于隧道分裂面之下，桩的沉降量较小，为5.53 mm。土体沉降大于桩基时，便产生负摩阻力，而桩由负摩阻力转为正摩阻力的交界点即为中性点[14]，该点处桩土无相对滑动且摩阻力为0，如图3b所示。中性点之上的负摩阻力自上而下相对位移逐渐减小并衰减至0；中性点以下的摩阻力先自上而下随桩土相对位移的增加从0增加到较大值，然后根据桩长的变化再减小，因此在中性点上下一定区域内为剪切力的过渡段。另外，中性点处桩身轴力最大，如图3c所示，因而中性点为桩身最不利位置。

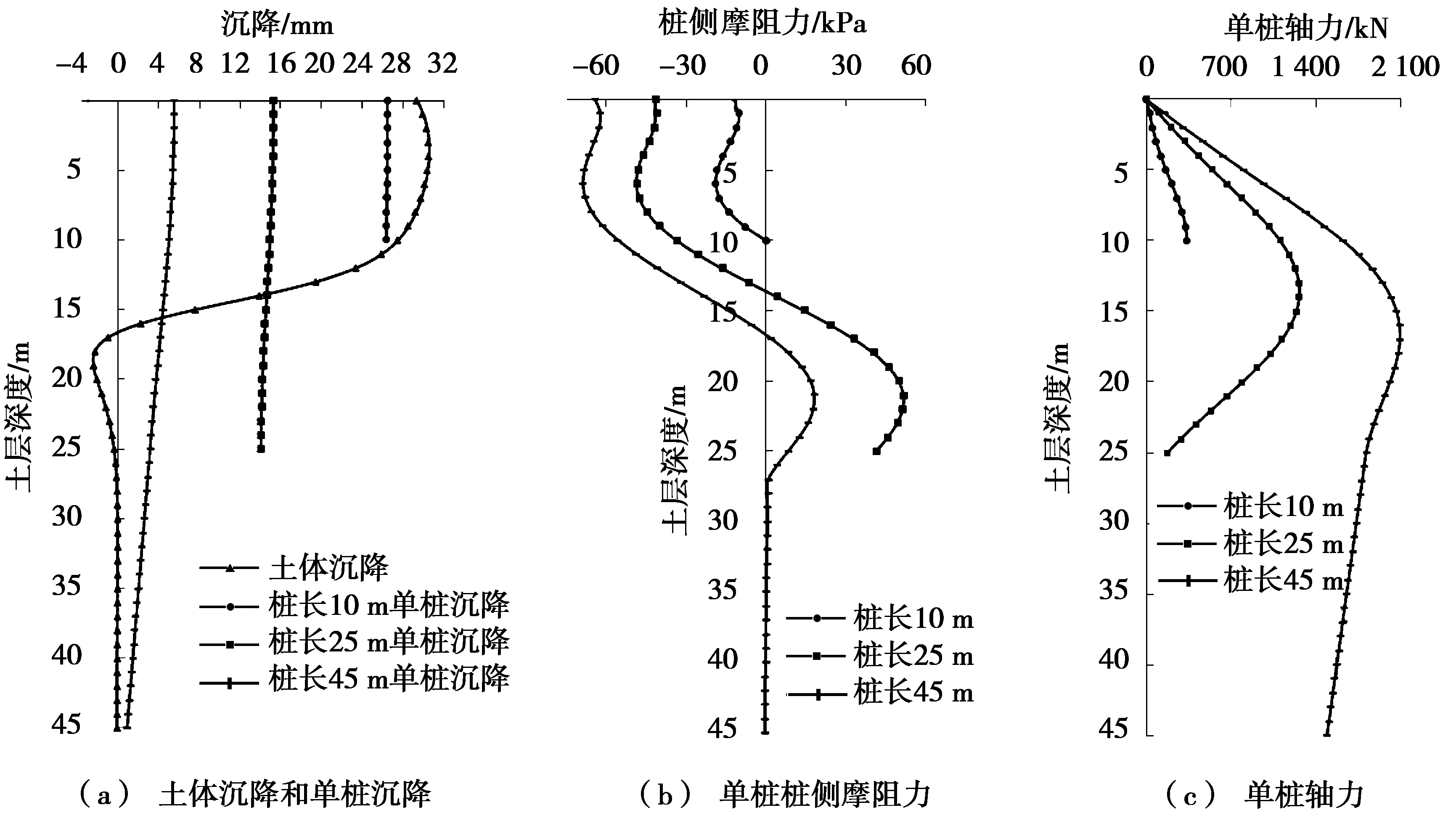
图3 X=4 m的土体位移及桩效应图

图4为桩隧空间布置及分裂面关系图。当土层性质和桩轴线与隧道轴线的水平距离一定时，分裂面主要与桩长有关。一般情况下，桩越短，土体位移均大于桩基位移，故桩基几乎位于破裂面之上，即桩基主要承受负摩阻力效应，如图4a所示。随着桩基长度的增加，其沉降随之较小，部分桩基位于分裂面之上(产生负摩阻力)，另一部分桩基位于分裂面之下(产生正摩阻力)，如图4b和图4c所示。通过对桩长的量化分析可知：桩长小于15 m(短桩)时，土体位移稍大于桩位移，单桩沉降很大；桩长超过15 m(中长桩、长桩)时，土体位移明显大于桩位移，部分桩段承受负摩阻力效应；且若桩长一定时，桩基距离隧道轴线越近，其桩位处土体位移越大，桩基沉降、摩阻力和轴力亦越大。

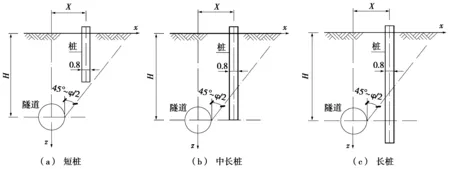
图4 桩隧空间布置及分裂面关系图

3 结论

(1)采用理论法分析隧道开挖引起桩土的相互作用，基于文克尔地基模型利用弹性地基梁理论，建立隧道开挖对单桩沉降的微分方程，根据常数变易法得出桩基沉降计算表达式，继而得出桩侧摩阻力及相应的桩周轴力。

(2)短桩的沉降很大，距离隧道越近，短桩几乎和土层同步沉降，土体沉降稍大于桩基沉降，且桩身大部分处于隧道破裂面之上。在桩中心线与隧道中心线水平距离一定的条件下，桩端与隧道的水平轴线的相对空间位置关系直接决定桩的沉降。

(3)距离隧道越近，土体沉降和桩基沉降均较大，桩土相对位移大，桩侧摩阻力越大。对于短桩而言，土体位移略大于桩基位移(即桩与土体相对位移较小)；随着桩长的增大(中长桩和长桩)，桩侧土体沉降明显大于桩沉降，在破裂面之上，桩一般承受负摩阻力的作用，而在破裂面之下，桩则承受正摩阻力的作用。负摩阻力增大了桩基附加轴力，且摩阻力为0时轴力最大。

[1] 马学宁,张沛云,贾喜翠,等.不同桩端下卧层桩基负摩阻力模型试验研究[J].铁道工程学报,2017,1(1):11-15.

[2] 刘开源,褚楚,韩晓雷,等.微型抗滑群桩受力特性模型试验[J].河南科技大学学报(自然科学版),2016,37(2):56-61.

[3] 丁小军,张海超,牛亚强.黄土地基竖向荷载下群桩基础承载特性室内试验研究[J].兰州交通大学学报,2015,34(4):80-85.

[4] 梅源,胡长明,李修波,等.黄土地基湿陷引发桩基负摩阻力的估算方法研究[J].西安建筑科技大学学报(自然科学版),2015,47(6):854-857.

[5] 赵明华,刘思思.多层地基单桩负摩阻力的数值模拟计算[J].岩土工程学报,2008,30(3):336-340.

[6] 聂如松,冷伍明.负摩阻力作用下的单桩竖向承载性状[J].中南大学学报(自然科学版),2013,44(4):1539-1543.

[7] 黄鹂,梁小勇,李娴.区间暗挖隧道侧穿既有桥桩施工扰动分析[J].河南科技大学学报(自然科学版),2016,37(4):66-70.

[8] 刘静,田晓艳.地铁浅埋暗挖施工对地表沉降及邻近桥基的影响[J].河南科技大学学报(自然科学版),2017,38(3):60-68.

[9] 周济民.盾构区间隧道下穿高架桥桩基群施工技术与环境影响预测[J].现代隧道技术,2016,53(1):165-172.

[10] 王立新.盾构超近距离穿越大型立交桩基群影响研究[J].地下空间与工程学报,2016,12(3):761-768.

[11] 赵明华,雷勇,刘晓明.基于剪切位移法的基桩负摩阻力计算[J].湖南大学学报(自然科学版),2008,35(7):1-6.

[12] RANDOLPH M F,WROTH C P.Analysis of vertical deformation of vertically loaded piles[J].Geotechnique engineering,ASCE,1978,104(12):465-488.

[13] LOGANATHAN N,POULOS H G,STEWART D P.Centrifuge model testing of tunneling-induced ground and pile deformations[J].Geotechnique,2000,50(3):283-294.

[14] 苟尧泊,俞峰,杨予.基坑开挖引起既有桩基侧摩阻力中性点位置分析[J].岩土力学,2015,36(9):2681-2687.

国家自然科学基金项目(51405385);陕西省教育厅专项科研计划基金项目(15JK1562)；西安石油大学博士科研启动基金项目(250205002)

田晓艳(1979-),女,陕西渭南人,讲师,博士,主要从事土木工程方面的教学与科研工作.

2017-04-18

1672-6871(2017)06-0049-04

10.15926/j.cnki.issn1672-6871.2017.06.010

TU473.1

A