一类有意识分类及干预措施的分数阶HIV/AIDS传染病模型
朱惠延,刘小佑,彭湘
(南华大学 数理学院,湖南 衡阳,421001)
一类有意识分类及干预措施的分数阶HIV/AIDS传染病模型
朱惠延,刘小佑,彭湘
(南华大学 数理学院,湖南 衡阳,421001)
在文章中,我们提出了一类具有意识分类和带有干预措施的分数阶HIV/AIDS传染病模型。讨论了模型无病平衡点和地方病平衡点的存在性,并且证明了地方病平衡点的依赖分数阶导数的阶数的稳定性。
HIV/AIDS流行病模型;分数阶微分方程;稳定性;干预措施
艾滋病是一种危害性极大的传染病,由感染艾滋病病毒(HIV病毒)引起。HIV是一种能攻击人体免疫系统的病毒。自从上世纪八十年代初被发现以来,世界各国的许多学者对其进行了大量的研究。鉴于目前没有针对该病治疗的特效药物,所以关于艾滋病的控制问题依然是采用预防为主的防治策略。
为了揭示艾滋病的传播规律并预测其流行趋势,许多学者针对导致艾滋病传播的不同因素建立了大量的有关艾滋病传播的数学模型[1-10]。另据相关研究表明,人们对传染病的认识程度以及主观预防意识等因素在疾病的传播中会起到一定的作用。最近几年来已有相关文献讨论了意识因素在部分传染病的传播中所起到的作用[10-13]。目前艾滋病疫情在少部分经济落后的国家呈高流行态势,在大部分国家(比如中国)艾滋病疫情呈低流行态势,这可能得益于相关政府或机构在宣传或干预艾滋病的防治工作中所起到的积极作用。
在本文中,我们将考虑一类具有意识分类和带有干预措施的分数阶HIV/AIDS传染病模型。首先,所研究区域内的人群被分为四类:即易感者S(t),“无意识”感染者I2(t)(对艾滋病不了解或不知道自己感染的感染者),“有意识”感染者I1(t)(知道自己感染并采取措施不去感染别人)和艾滋病患者A(t)。由此可假设艾滋病的传播只发生在易感者S(t)和“无意识”感染者I2(t)之间(这是最主要的传播类型)。另外,政府和相关机构会通过宣传教育、高危人群艾滋病感染筛查、以及定向跟踪治疗等方式进行艾滋病的干预防治。具体模型如下:
(1)
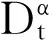
在本文中,我们将讨论上述模型(1)的无病平衡点和地方病平衡点的存在性并证明其地方病平衡点具有依赖分数阶导数的阶数的稳定性。
1 预备知识
定义1[6,9]函数g:R+→R的α>0阶分数阶积分定义为

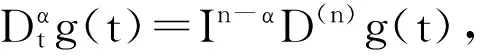
定理1[6]考虑如下分数阶微分方程组
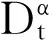

(2)
2 模型平衡点的存在性
为以下书写方便,引入记号Μ=δ+θ+d,Ν=δ+d和Ρ=a-f。模型(1)的平衡点可通过求解下面非线性方程组得到
若I2=0,可知I1=0,A=0和S=m/d。即模型(1)总有无病平衡点EP0=(m/d,0,0,0)。若I2≠0,可推出

以及一个关于I2的一元二次方程
(3)
在这里

注1 在本模型中可假设a-f>0。若a-f≤0,则可知方程组(1)中第二式的右端项恒小于或等于零,那么状态变量I2最终将减小到零,即该疾病最终会消失。此时模型(1)只具有无病平衡点。
定义模型(1)的基本再生数

(4)
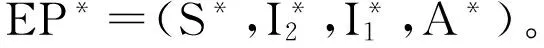
证明:显然一元二次方程(3)的二次项系数H和一次项系数J都为正。把常数K改写成

另引入一元二次式
显然Q(I2)=R0与一元二次方程P(I2)是同解的。一元二次式Q(I2)的图形开口向上,且有Q(0)=1,其顶点坐标为(I2-min,Q(I2)-min),其中
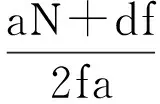

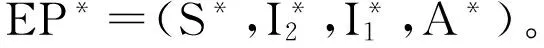
1.2.1.2.3清扫由副组长列出值日表,落实到人,严格执行治疗室的清洁工作,建立卫生规范,打扫要彻底,脏污要清除干净,不留死角,桌面及地面每日用消毒剂擦拭两次,同时也可要求保洁人员参与其中,共同维护工作场所干净、明亮,对于医疗垃圾处理,要遵守相关规定严格执行。
3 模型平衡点的稳定性
方程组(1)的Jacobian矩阵为:
(5)
定理3 若0 引入一元三次多项式方程Q(λ)=λ3+a2λ2+a1λ+a0=0。由a2,a1和a0的表达式可得这三个数都为正。此时,笛卡尔符号规则 (Descartes’ rule of signs)告诉我们,三次方程Q(λ)要么有三个负实根,要么有一个负实根和两个共轭复根。 情形(1):三次方程Q(λ)有三个负实根。由特征多项式P(λ)与Q(λ)的关系可知,特征方程P(λ)=0有4个负实根。对0<α<1,都满足定理1中式(2)。此时,模型(1)的唯一地方病平衡点EP*是渐近稳定的。 情形(2):三次方程Q(λ)有一个负实根和两个共轭复根。此时,不妨假设这三个根为λ1=-x,λ2,3=y±zi。由根与系数的关系(Vieta’s formulas)可得:a2=x-2y,a1=y2+z2-2xy和a0=x(y2+z2)。因为a2,a1>0,所以有x>2y,y2+z2>2xy和 上式表明sec2(Argλ2,3)>4。即有tan2(Argλ2,3)>3,所以2π/3>Argλ2,3>π/3。因此当0<α≤2/3时,特征多项式P(λ)有2个负实根和2个共轭复根且它们的辐角满足定理1中式(2)。此时模型(1)的唯一地方病平衡点EP*是渐近稳定的。 当然,如果能选择模型参数使a2a1>a0,此时由劳斯-赫尔维茨判据(Routh-Hurwitz criterion)可知特征多项式P(λ)有2个负实根和2个具有负实部的共轭复根,定理1中式(2)也将成立。此时模型(1)的唯一地方病平衡点EP*是渐近稳定的。综上所述,该定理得证。 在本文中,我们考虑了一类具有意识分类和带有干预措施的分数阶HIV/AIDS传染病模型。给出了其平衡点存在的充分条件,并证明了平衡点的渐近稳定性。通常来说,艾滋病防治机构要先综合考虑很多的因素后才采取适当干预措施。在本模型中,我们采用了非线性项fI2(S+I1+I2)来模拟对艾滋病防控的干预措施,目的是减少目标人群I2的数量,以期望降低易感者感染艾滋病毒的几率。另外,把基本再生数R0看作干预强度量f的函数。因为 上式说明R0关于f是减函数。这表明加强干预措施可以减少R0的值,即可减少疾病的流行。这也说明模型的假设是合理的,模型的研究结果对于艾滋病的防治工作有一定的指导意义。 [1]VALLE S D,EVANGELISTA A M,VELASCO M C,et al.Effects of education,vaccination and treatment on HIV transmission in homosexuals with genetic heterogeneity [J].Mathematical Biosciences,2004,187(2):111-133. [2]CAI L M,GUO S L,WANG S P.Analysis of an extended HIV/AIDS epidemic model with treatment [J].Applied Mathematics and Computation,2014,236(4):621-627. [3]NARESH R,TRIPATHI A,SHARMA D.A nonlinear HIV/AIDS model with contact tracing [J].Applied Mathematics and Computation,2011,217(23):9575-9591. [4]BARYARAMA F,LUBOOBI L S,MUGISHA J Y T.Periodicity of the HIV/AIDS epidemic in a mathematical model that incorporates complacency [J].American Journal of Infectious Diseases,2005,1(1):55-60. [5]HOVE-MUSEKWAA SD,NYABADZA F.The dynamics of an HIV/AIDS model with screened disease carriers [J].Computational and Mathematical Methods in Medicine,2015,10(4):287-305. [6]ROSTAMY D,MOTTAGHI E.Stability analysis of a fractional-order epidemics model with multiple equilibriums [J].Advances in Difference Equations,2016,2016(1):1-11. [7]SEIDU B,MAKINDE O D,DAABO M I.Optimal control analysis of an HIV/AIDS model with linear incidence rate [J].Journal of Mathematical and Computational Science,2016,6(1):58-75. [8]ZHU H Y,ZOU X F.Impact of delays in cell infection and virus production on HIV-1 dynamics [J].Mathematical Medicine and Biology:A Journal of the IMA,2008,25(2):99-112. [9]KOU C H,YAN Y,Liu J.Stability analysis for fractional differential equations and their applications in the models of HIV-1 infection [J].Computer Modeling in Engineering and Sciences,2009,39(3):301-317. [10]ROY P K,SAHA S,BASIR F A.Effect of awareness programs in controlling the disease HIV/AIDS:an optimal control theoretic approach [J].Advances in Difference Equations,2015,2015(1):1-18. [11]ZUO L X,LIU M X.Effect of awareness programs on the epidemic outbreaks with time delay [J].Abstract and Applied Analysis,2014,2014:1-8. [12]ZUO L X,LIU M X,WANG J Q.The impact of awareness programs with recruitment and delay on the spread of an epidemic [J].Mathematical Problems in Engineering,2015,2015:1-10. [13]朱惠延,彭湘,刘小佑.一类具有意识分类的分数阶HIV/AIDS传染病模型的研究[J].南华大学学报(自然科学版),2016,30(4):62-66. On a class of HIV/AIDS epidemic fractional differential models with awareness and intervention measures ZHU Huiyan,LIU Xiaoyou,PENG Xiang (School of Mathematics and Physics,University of South China,Hengyang 421001,China) In this paper,a class of HIV/AIDS epidemic fractional differential models with awareness and intervention measures was considered.We discussed the existence of disease-free equilibrium points and endemic equilibrium points and proved their stability. HIV/AIDS epidemic model; fractional differential equations; stability; intervention measures 1672-7010(2017)03-0001-05 2017-04-06 国家自然科学基金青年项目(11501284);湖南省自然科学基金项目(2015JJ6095);湖南省教育厅科学研究重点项目(14A128);湖南省教育厅科学研究优秀青年项目(16B224) 朱惠延(1962-),女,湖南衡阳人。教授,博士,主要从事生物数学方面研究; 刘小佑(1983-),男,湖南耒阳人。副教授,博士,主要从事微分方程方面研究。 O175.1 A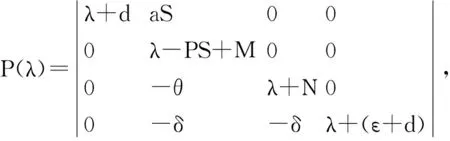

4 结语


