Merton随机利率模型下的欧式期权定价
郭志东
(安庆师范大学 数学与计算科学学院,安徽 安庆,246000)
Merton随机利率模型下的欧式期权定价
郭志东
(安庆师范大学 数学与计算科学学院,安徽 安庆,246000)
利用偏微分方程的方法研究了Merton利率模型下的欧式期权定价问题。得到了此模型下欧式看涨期权所满足的Black-Scholes方程,并给出了欧式看涨期权的定价公式。在文章的最后给出了相关的数值结果并探讨了该模型下的隐含波动率问题。
期权定价;Merton利率模型;隐含波动率
期权(Option),是一种选择权,指是一种能在未来某特定时间以特定价格买入或卖出一定数量的某种特定商品的权利。期权按照合约中购入和销售原生资产可分为看涨期权(call option)和看跌期权(put option)。看涨期权是一张在确定时间按照确定价格有权购入一定数量原生资产的合约。看跌期权一张在确定时间按照确定价格有权销售一定数量原生资产的合约。期权按照合约中有关实施的条款可分为欧式期权(European options)和美式期权(American options)。欧式期权是只能在合约规定的到期日实施的期权。美式期权是能在合约规定的到期日(包括到期日)前的任何一个交易日实施的期权。
定义1[1]如果随机过程B(t)满足
1)轨线连续:B(0)=0,B(t)是t的连续函数。
2)增量正态分布:对固定的t,B(t)~N(0,t),以及对t>s有
B(t)-B(s)~N(0,t-s)。
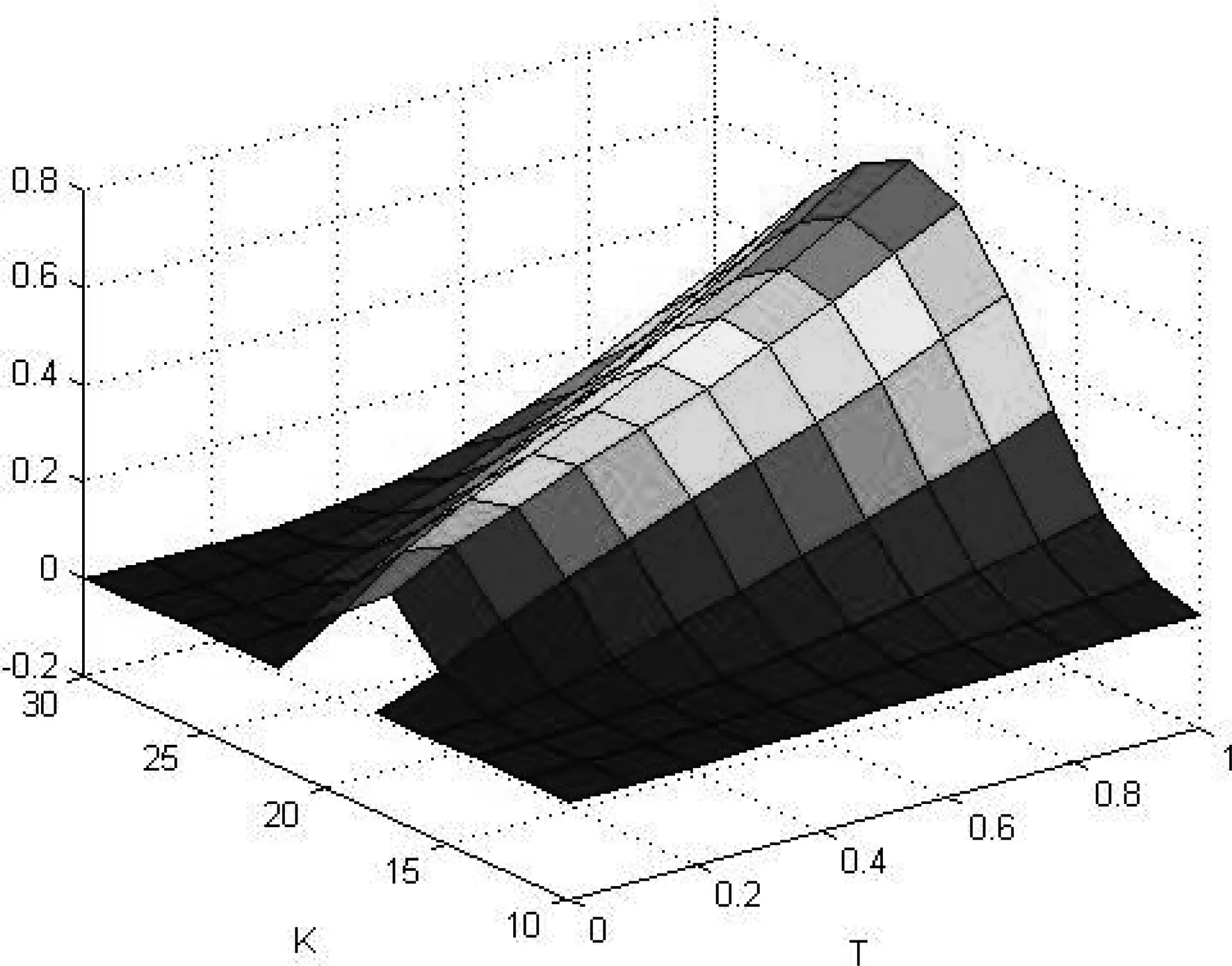
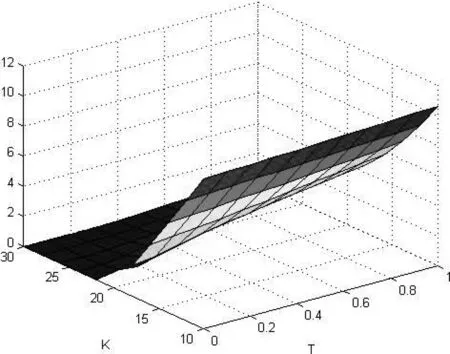
3)增量独立:B(tn)-B(tn-1),B(tn-1)-B(tn-2),…B(t2)-B(t1)与W(t1)都是相互独立的(0 则称B(t)为布朗运动或Wiener过程。 在经典的Black-Scholes[2]期权定价模型中,标的股票的价格St服从如下的几何布朗运动 dSt=μStdt+σStdB(t), 这里B(t)是标准布朗运动,期望回报率μ和波动率σ都是常数。 Black-Scholes模型中的一个重要假设是在期权的有效期内无风险利率r是常数。然而,这一假设不符合现实金融市场中的情形,利率r是随着市场不断变化的。因此,在期权定价模型中应把利率的随机性考虑进去。由于利率本身是不可交换的,在金融衍生产品的定价中常借助零息票债券来给出随机利率模型下的衍生产品定价。Merton[3]在随机利率的假设下给出了零息票债券的定价公式。本文在Kung~和Lee[4]、Cui and Mcleish[5]和Guo[6]的基础上利用偏微分方程的方法研究 Merton[7]随机利率模型下欧式期权的定价问题。 本文的结构如下:在第二节中我们给出欧式看涨期权在Merton随机利率模型下的定价公式。在第三节我们将讨论该模型下的隐含波动率问题并给出相关的一些数值结果。 在本节中,假设利率r(t)满足下面的的Merton利率模型,即 dr(t)=μrdt+σrdBr(t), (1) 标的股票的价格S(t)满足下面的随机微分方程 dS(t)=μsS(t)dt+σsS(t)dBs(t), (2) 这里μr,σr,μS和σs是常数,Br(t)和Bs(t)是标准的维纳过程,并且这里我们假设Br(t)和Bs(t)是相互独立的。 记P(r,t;T)是在到期T换取1元的零息票债券在t时的价格。则由Kung~和Lee[4]或Merton[7]可知 (3) 这里τ=T-t。此外,这里我们假设交易是连续的并且没有交易成本、保证金和税费;期权在整个有效期内没有红利;所有投资者都可以以相同的短期利率借入或借出资金。 引理1[1](It公式) 设Vt=V(t,St),V是二元可微函数,若随机过程St满足随机微分方程 dSt=μ(t,St)dt+σ(t,St)dBt, 记c(S,r,t)为欧式看涨期权的价格,K为期权的敲定价格,期权的到期日为T。则在上面的假设下,我们可得: 定理1 当r(t)和S(t)分别满足(1)和(2)时,欧式看涨期权的价格c(S,r,t)满足下面的偏微分方程 (4) 且边界条件为 c(S,r,t)=(S-K)+。 (5) 进一步,我们可得 c(S,r,t)=SN(d1)-KP(r,t;T)N(d2), (6) 其中, (7) (8) 证明 考虑包含一份欧式看涨期权、Δ1t份标的股票和Δ2t份零息票债券的投资组合Π。在时间t时投资组合Π的价值为 Πt=c(S,r,t)-Δ1tSt-Δ2tP(r,t;T)。 (9) 因此,由引理1有 dΠt=dc(S,r,t)-Δ1tdSt-Δ2tdP(r,t;T) (10) 取 (11) 则 dΠt=dc(S,r,t)-Δ1tdSt-Δ2tdP(r,t;T) (12) 由 Ε(dΠt)=r(t)Πdt=r(t)[c(S,r,t)-Δ1tSt-Δ2tP(r,t;T)]dt, (13) 则由等式(11-13),可得c(S,r,t)满足 (14) 边值条件为 c(S,r,t)=(S-K)+。 (15) 为了解边值问题(14-15),作下面的变量替换 (16) 通过计算可得 把上面这些等式代入等式(12)和(13),化简后可得 (17) ĉ(y,T)=(y-K)+。 (18) 解边值问题(17-18)并换回原来的变量可得 c(S,r,t)=SN(d1)-KP(r,t;T)N(d2), (19) 其中 (20) (21)证毕。 2.1 隐含波动率 推论1 当t=0时欧式看涨期权在Merton随机利率模型下的的价格cMerton为 (22) 其中 (23) (24) (25) 这里 (26) 又在t=0时经典的Black-Scholes公式为 (27) 其中 (28) (29) 对比经典的Black-Scholes公式我们可以看出σim即为相对经典Black-Scholes模型的隐含波动率。同样这里我们不妨称rim为相对经典Black-Scholes模型的隐含利率。 2.2 数值计算 在本节中,我们选取与Kung 和Li[4]相同的参数值。这里,r(0)=0.06,μr=0.02,σr=0.2,σs=0.3,T=1,K=15,S0=20。 图1 所示为欧式看涨期权价格在Merton随机利率模型下与在经典Black-Scholes模型下的价格之差,即cMerton-cBS 。从中我们可以看出当K,T比较大时cBS明显小于cMerton。Fig.1 The difference between the price of European call option under the Merton short rate model and the price of European call option under the classical model,i.e.cMerton-cBS. 图2 所示为K,T对欧式看涨期权在Merton随机利率模型下的价格cMerton的影响Fig.2 The European call option price under the Merton short rate model cMerton,according to the expiration date T and the strike price K. 本文我们用偏微分方程的方法给出了欧式看涨期权在Merton随机利率模型下的定价公式,并给出了相关数值计算结果。我们的数值结果显示对于价外看涨期权来说,经典的Black-Scholes 模型给出的定价要明显低于Merton随机利率模型所给出的定价。 [1]姜礼尚,期权定价的数学模型和方法[M].北京:高等教育出版社,2003. [2]BLACK F,SCHOLES M.The pricing of options and corporate liabilities[J].Journal of Political Economy,1973,81(3):637-654. [3]MERTON RC.Theory of rational option pricing [J].Bell Journal of Economics,1973,4(1): 141-183. [4]KUNG JJ,LEE LS.Option pricing under the Merton model of the short rate[J].Mathematics & Computers in Simulation,2009,80(2):378-386. [5]CUI Z,MCLEISH D,RATES SI,et al.Comment on‘option pricing under the Merton model of the short rate’by Kung and Lee[J].Mathematics & Computers in Simulation,2011,81:1-4. [6]GUO Z.Option pricing under the Merton model of the short rate insubdiffusive Brownian motion regime[J].Journal of Statistical Computation and Simulation,2016:1-11. [7]MERTON RC.A dynamic general equilibrium model of the asset market and its application to the pricing of the capital structure of the firm [J].Sloan School of Management Working Paper,1970,11:497. Option pricing under the Merton short rate model GUO Zhidong (College of Mathematics & Computation Science,AnQing Normal University,Anqing 246000,China) Used the method of PDE to consider the option pricing of European option under the Merton short rate model.The Black-Scholes equation which European call options satisfy was derived,and the formula of European call option was given.At the end of the paper,some relative numerical results were given and the implied volatility was talked. option pricing; Merton model of short rate; implied volatility 1672-7010(2017)03-0023-05 2017-03-24 国家自然科学基金资助项目(11626031);安徽省教育厅自然科学项目(KJ2016A428/AQKJ2015B011) 郭志东(1986-),男,山东济宁人。讲师,博士,主要从事偏微分方程理论及应用方面研究。 O29 A1 Merton随机利率模型下欧式看涨期权定价公式
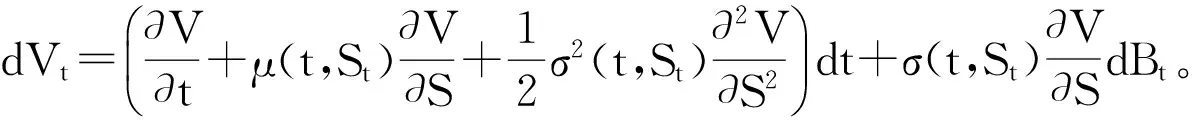
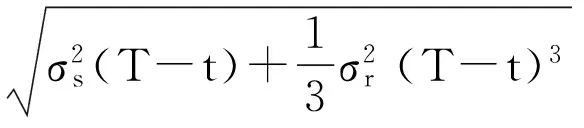
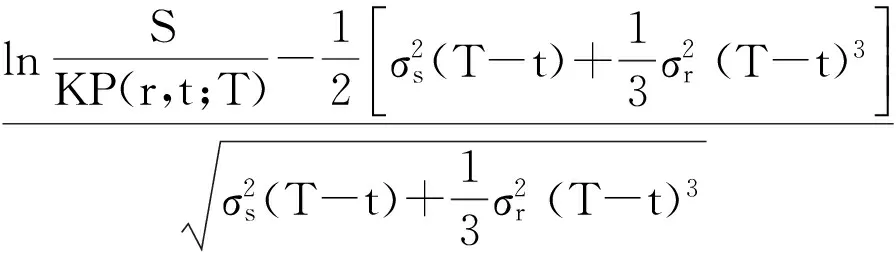
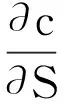
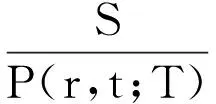
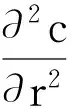


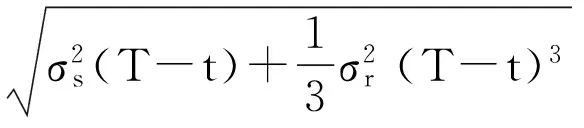
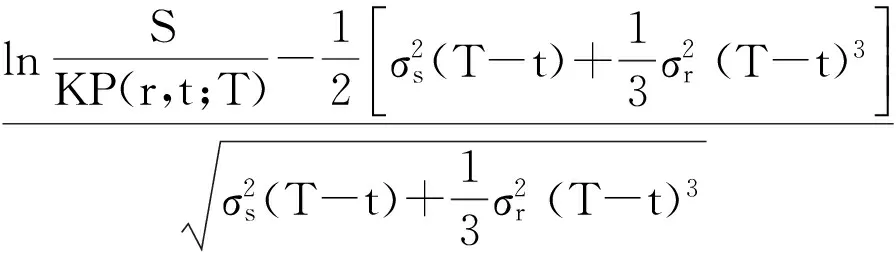
2 隐含波动率和数值计算
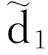
3 结论

