关于图的拉普拉斯谱半径

周后卿

(邵阳学院 理学院，湖南 邵阳，422000)



关于图的拉普拉斯谱半径

周后卿

(邵阳学院 理学院，湖南 邵阳，422000)

对图的拉普拉斯谱半径研究状况做了一个梳理，主要介绍了近几年来对图的拉普拉斯谱半径和拟拉普拉斯谱半径的界的研究所取得的成果，同时指出一些未曾解决的问题和今后的研究方向。

拉普拉斯矩阵；拟拉普拉斯矩阵；谱半径

图谱理论是图论的一个重要的研究领域,它在计算机科学、通信网络、信息科学、量子化学以及统计力学中均有着广泛的应用。利用代数理论和技巧,结合组合数学理论来研究图谱、图的结构性质以及与图的其它不变量(如色数、度序列、直径、围长、连通度等)之间的关系，将图与网络的代数性质与其拓扑性质紧密地结合在一起。在图谱理论中,为了研究图的性质,常引入了一些矩阵,如图的邻接矩阵、拉普拉斯矩阵等等,这些矩阵与图的结构有着密切的联系。研究的主要途径是：通过图的邻接矩阵或拉普拉斯矩阵表示，建立图的拓扑结构与图的矩阵表示的置换相似不变量之间的联系，通过矩阵论，特别是非负矩阵理论和对称矩阵理论，以及组合矩阵论中的经典结论，用于图的拓扑结构的研究；同时也将图论中的经典结果用于非负矩阵理论和组合矩阵论，从而推动这些理论的发展。

图的拉普拉斯谱是图谱理论主要研究内容之一。拉普拉斯矩阵是黎曼流形上的拉普拉斯算子在图上的离散形式。早在19世纪中叶，G.Kirchhoff就利用拉普拉斯矩阵谱来研究电流网络，并给出了著名的矩阵树定理。但关于拉普拉斯矩阵谱研究的兴起却是近几十年的事情，正如Mohar[1]所说，拉普拉斯特征值比邻接矩阵特征值更能反映图的特质，而且比图的邻接谱更加自然和重要。对图的邻接矩阵和拉普拉斯矩阵特征值而言，最大特征值(也即图的谱半径)是所有特征值中最重要的一个量。所以，几十年来学者们对图的拉普拉斯谱半径情有独钟，孜孜以求之，产生了许多深刻的结果。随着研究方法的增加和科学技术的进步，借助计算机，更是得到了许多精确的结果。

本文梳理近些年来，专家学者在图的拉普拉斯谱以及图的无符号拉普拉斯谱领域研究所取得的一些结果，以期对后来的研究有点帮助。

1 关于图的拉普拉斯谱半径的上界

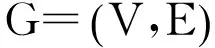
关于图的拉普拉斯谱半径上界，学者们就一般的图给予了研究，并且对树、单圈图、双圈图、二部图等特殊图也做了讨论,得到了许多深刻的结果。

Anderson and Morley[2]利用相邻两个顶点度给出了一个上界

等式成立当且仅当G是一个正则二部图或半正则二部图。

Merris[3]利用平均度改进了上述上界，得到了

这里mu表示与顶点u相邻的顶点的平均度。

Das[4]在文献[2]的基础上做了改进，证明了：设G是一个具有n个顶点的连通图。则

后来，Li and Zhang[5]在上述文献的基础上，得出了

等式成立当且仅当G是一个正则二部图。

利用最大、最小、平均度，L.Shi[6]证明了：设G是一个具有n个顶点，直径为D，最大度为Δ，最小度为δ，平均度为d的非正则连通图。则

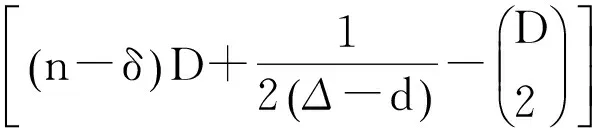
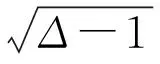
同年，Ji-Ming Guo[8]利用匹配数证明了 ：

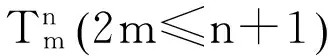
对于单圈图，Lihua Feng[9]等人讨论了具有给定独立数的单圈图的拉普拉斯谱半径问题，他们得出了下列结果：

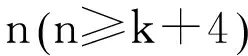
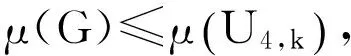
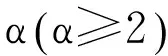
对于二部图，R.Grone，R.Merris，V.S.Sunder[10]等人获得了如下结论：

设G是一个连通图，则μ(G)≤q(G)，等式成立当且仅当G是一个二部图。

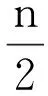
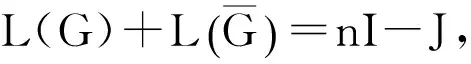
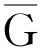
对于两个图的卡氏积图，文献[12]获得了下列结果;设简单图G具有n顶点m条边，图H具有p个顶点q条边，那么G和H的Cartesian积图G×H的拉普拉斯最大特征值满足下列不等式

2 拉普拉斯谱半径的下界

对于图的谱半径的下界，也有很多结论。

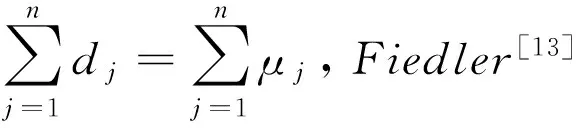
Kamal Lochan Patra and Binod Kumar Sahoo[15]讨论了具有固定围长的单圈图的最小拉普拉斯谱半径问题，他们得出了下列结论

设G是一个具有n个顶点围长为g，且与Un,g不同构的单圈图。则

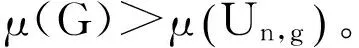
文献[8]还证明了：设G是一个连通的二部图，H是G的子图，则μ(G)≥μ(H),等式成立当且仅当H=G。

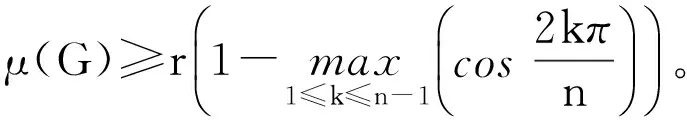
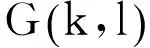
3 拟拉普拉斯谱半径

(1)q(G)=0当且仅当G不含边。

(2)如果G的所有补图都是路，则0

(3)对连通图G，q(G)=4当且仅当G是一个圈或者一个完全二部图K1,3。

文献[27]证明了：设图G具有n(n≥4)个顶点，那么，G的拟拉普拉斯谱半径q(G) 满足下列不等式

定义图G中的一条路，它是一个点序列v0v1…vk+1(k≥2)，v0,v1,…,vk互不相同，v0和vk+1的度至少为3，dvi=2，且vi-1与vi(i=1,2,…,k)邻接。若G是一个连通图，uv是G中路上的一条边，将uv细分为uw，wv后所得的图记作Guv。文献[28]证明了

4 结束语

上面我们把近些年来，有关图的拉普拉斯谱半径和拟拉普拉斯谱半径的一些研究成果做了一个大致的梳理。他们所采取的方法，一般是给出限制条件，先将图限定具有某种结构或某种特征；然后再利用矩阵分析的方法来讨论。关于图的特征值，它是图谱理论中的一个重要研究课题，还有许多问题值得人们去探索，去解决。对拉普拉斯谱或拟拉普拉斯谱的排序，刻画具有最大或最小拉普拉斯谱半径的极图是一些有趣而未曾完全解决的问题。再就是图的拉普拉斯或拟拉普拉斯谱半径与图的其他参数之间的关系，也是研究方向之一。

[1]MOHAR B,ALAVI Y,CHARTRAND G,et al.The Laplacian spectrum of graphs[M].Graph theory，Combinatorics and Applications，1991,18(7):871-898.

[2]ANDERSON W N，MORLEY T D.Eigenvalues of the Laplacian of a Graph[J].Linear and Multilinear Algebra,1985，18(2):141-145.

[3]MERRIS R.A note on Laplacian graph eigenvalues[J].Linear Algebra and its Applications， 1998，285(1-3):33-35.

[4]DAS K.An improved upper bound for Laplacian graph eigenvalues[J].Linear Algebra and its Applications，2003,368(2):269-278.

[5]LI J S，ZHANG X D.On the Laplacian eigenvalues of a graph [J].Linear Algebra and its Applications，1998，285:305-307.

[6]SHI Lingsheng.The spectral radius of irregular graphs[J].Linear Algebra and its Applications,2009,431(1-2):189-196.

[7]STEVANOVIC D.Bounding the largest eigenvalue of trees interms of the largest vertex degree[J].Linear Algebra and its Applications，2003，360(2):35-42.

[8]GUO Ji Ming.On the Laplacian spectral radius of a tree[J].Linear Algebra and its Applications，2003，368(2):379-385

[9]FENG Lihua，YU Guihai,Aleksandar Ilic.The Laplacian spectral radius for unicyclic graphs with given independence number[J].Linear Algebra and its Applications，2010，433(5):934-944

[10]GRONE R,MERRIS R，SUNDER V S.The Laplacian spectrum of a graph[J].Siam Journal on Matrix Analysis and Applications，2006，2(11):218-238.

[11]LI Jianxi，SHIU Wai Chee,CHAN Wai Hong.On the Laplacian spectral radii of bipartite graphs[J].Linear Algebra and its Applications，2011，435(9):2183-2192.

[12]周后卿.Cartesian 积图的最大拉普拉斯特征值[J].邵阳学院学报(自然科学版)，2011，8(1):5-7.

[13]FIEDLER M.Algebraic Connectivity of Graphs[J].Czechoslovak Mathematical Journal，1973,23(23)：298-305.

[14]GRONE R，MERRIS R.The Laplacian spectrum of a graph II[J].Siam Journal on Mathematics,1994，7(2):221-229.

[15]KAMAL Lochan Patra,BINOD Kumar Sahoo.Minimizing Laplacian spectral radius of unicyclic graphs with fixed girth[J].Czechoslovak Mathematical Journal，2013，63(4):909-922.

[16]周后卿．循环图的无符号拉普拉斯谱半径[J]．邵阳学院学报(自然科学版)，2015，12(4):3-6．

[17]LU Mei,ZHANG Lian Zhu，TIAN Feng.Lower bounds of the Laplacian spectrum of graphs based on diameter[J].Linear Algebra and its Applications，2007，420(2-3):400-406.

[18]GUO J M.The effect on the Laplacian spectral radius of a graph by adding or grafting edges[J].Linear Algebra and its Applications，2006，413(1):59-71.

[19]GUO Jiming，LI Jianxi，SHIU Waiche.The smallest Laplacian spectral radius of graphs with a given clique number[J].Linear Algebra and Its Applications，2012，437(4)：1109-1122.

[20]ZHANG Jingming，GUO Jiming.The Signless Laplacian spectral radius of bicyclic graphs with order n and girth g[J].Ars Combinatoria，2015，123：33-40.

[21]ZHANG Jingming，HUANG Tingzhu，GUO Jiming.On the signless Laplacian spectral radius of unicyclic graphs with fixed matching number[J].Publications de l’Institut Mathématique，2015，97(111):187-197.

[22]YUAN Xiying，GUO Jiming.Note on the kth Laplacian eigenvalues of trees with perfect matchings[J].Linear Algebra and Its Applications，2015，483:115-127.

[23]ZHANG Xiaodong.The signless Laplacian spectral radius of graphs with given degree sequences[J].Discrete Applied Mathematics，2009，157(13):2928-2937.

[24]CVETKOVI’C D,ROWLINSON P，SIMI’C S K.Eigenvalue bounds for the signless Laplacian[J].Publications de l’Institut Mathématique，2007，81 (95) :11-27.

[25]CVETKOVI’C D，ROWLINSON P,SIMI’C S K.Signless Laplacians of finite graphs[J].Linear Algebra and Its Applications，2007,423 (1):155-171.

[26]XING Rundan，ZHOU Bo.Laplacian and signless Laplacian spectral radii of graphs with fixed domination number[J].Mathematische Nachrichten，2015，288(4):476-480.

[27]CHEN Y.Properties of spectra of graphs and line graphs[J].Applied Mathematics A Journal of Chinese Universities Series B，2002，17(3):371-376.

[28]FENG L,YU G.The signless Laplacian spectral radius of unicyclic graphs with graph constraints[J].Kyungpook Mathematical Journal，2009，49(1):123-131.

On the Laplacian spectral radius of graphs

ZHOU Houqing

(School of Sciences，Shaoyang University，Shaoyang 422000，China)

Analyzing the research status of Laplacian spectral radius of graphs，mainly introduced research achievements of bounds of the Laplacian and signless Laplacian radius of graphs in recent years .At the same time pointed out some unsolved problems in the study and proposed the future research direction.

Laplacian matrix; signless Laplacian matrix; spectral radius

1672-7010(2017)03-0006-06

2017-03-20

湖南省教育厅科学研究项目(15C1235;16C1434)；邵阳市科技局科技计划指导项目(2016ZD09)

周后卿(1963-),男,湖南新邵人。教授,硕士,从事图论及其应用研究。

O157.5

A