如何利用函数的单调性解题
■陕西省西乡县第二中学 闫 俊
如何利用函数的单调性解题
■陕西省西乡县第二中学 闫 俊
函数的单调性是函数的重要性质之一,也是高考考查函数时重点考查的内容。在高考试题中我们通常见到的函数单调性的应用不外乎求参数的取值范围、解不等式与求函数的最值这三类问题。应当强调的是,解决这三类问题时应当重视函数单调性的定义、函数的定义域,以及数形结合思想。
一、利用函数的单调性求参数的取值范围
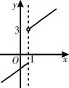
图1
解析:若设g(x)=(a-2)x-1,h(x)= x+2。因为函数f(x)在(-∞,+∞)上单调递增,所以a-2>0,即当a>2时,g(x)在(-∞,1]上单调递增。而在(1,+∞)上h(x)也是单调递增的,于是h(x)>h(1)=3。要使函 数 f (x) =在(,-∞ +∞)上单调递增,如图1所示,则需g(1)≤h(1),即a-3≤3,所以a≤6。综上,实数a的取值范围是2 评注:由以上解题过程可以看出,对含参数的分段函数利用其单调性求参数的取值范围,应抓住两点:一是严格遵循函数单调性的定义;二是结合函数图像观察约束参数的限制条件,也就是关于参数的不等式。 首先,要做一下强调,如果是利用函数的单调性解不等式,则一定要注意函数的定义域,否则极易出现错解。 已知函数f(x)是增函数,定义域为(0,+∞),且f(4)=2,f(xy)=f(x)+ f(y),求满足f(x)+f(x-3)≤2的x的取值范围。 解析:因为f(x)+f(x-3)≤2,f(xy)= f(x)+f(y),所以f[x(x-3)]=f(x)+ f(x-3)≤2=f(4)。又f(x)在(0,+∞)上是增函数,所以x(x-3)≤4,解得-1≤x≤4。由题意知,满足f(x)+f(x-3)≤2,则即解得3 评注:函数的单调性是相对于函数定义域内某个子区间而言的“局部”性质,它反映了函数在某区间上函数值的变化趋势。当我们利用函数的单调性解决问题时,如果不顾函数的定义域去盲目解题,就会造成错解。 评注:函数单调性在解答过程中的运用主要体现在通过题设所给函数等价变形为,把原问题转化为对函数单调性的讨论,明确单调性后利用单调性达到求解最值的目的。 (责任编辑 王福华)二、利用函数的单调性解不等式
三、利用函数的单调性求函数的最值

