基于双树复小波包自适应Teager能量谱的滚动轴承早期故障诊断
任学平, 王朝阁, 张玉皓, 王建国
(内蒙古科技大学 机械工程学院,内蒙古 包头 014010)
基于双树复小波包自适应Teager能量谱的滚动轴承早期故障诊断
任学平, 王朝阁, 张玉皓, 王建国
(内蒙古科技大学 机械工程学院,内蒙古 包头 014010)
针对滚动轴承早期故障特征信息难以识别以及带通滤波器参数设置依赖使用者经验等造成共振带不能有效确定并自适应提取的问题,提出了频带幅值熵的概念。在此基础上,将双树复小波包变换和Teager能量谱结合,提出了基于双树复小波包变换自适应Teager能量谱的早期故障诊断方法。该方法首先利用双树复小波包将采集到的振动信号进行分解,并计算各子带的频带幅值熵。然后将熵值按升序排列后依次作为阈值,提取频带幅值熵大于或等于阈值的子带,依据峭度指标确定最佳熵阈值和双树复小波包最佳分解层数,从而自适应并有效地提取出共振带。最后对共振带进行Teager能量谱分析,即可从中准确地识别出轴承的故障特征频率。通过信号仿真与工程实验数据分析验证了该方法的有效性与优越性。
频带幅值熵;双树复小波包;Teager能量谱;自适应共振带提取;轴承故障
滚动轴承是旋转机械中重要的元件,它为旋转结构提供可靠稳定的支撑,设备运行过程中的大部分能量都要传递到轴承上。当轴承出现故障时,设备及其他零件将很容易受到毁坏,这会导致人员和经济遭受巨大损失,后果极其严重。因此,能够准确、有效地检测出轴承早期故障对预防事故的发生具有十分重要的意义[1-2]。
当滚动轴承出现点蚀、剥落、裂纹等局部损伤时,滚动体在工作过程中通过损伤部位会产生周期性冲击,形成低频振动。而在故障萌发的初期阶段,故障特征信号往往被机械系统多干扰源和强噪声所淹没,会导致低频段的谐波故障特征频率非常微弱,不能够作为诊断故障的有效判据[3]。由于滚动轴承局部损伤诱发的周期性冲击频率范围较宽,常常会激起轴承系统的固有振动,由于阻尼的作用,这种冲击所激发的系统自身响应表现为一种高频衰减振动,并会出现复杂的调制现象[4]。
包络解调是滚动轴承故障中常用的精确诊断方法,它对于比较严重的轴承故障有着较好的分析效果,但对比较微弱的早期故障有一定的局限性[5]。为此,文献[6]提出了基于Teager能量谱的滚动轴承故障诊断方法,能够准确地诊断滚动轴承元件故障,并与包络谱方法进行了对比,结果显示,其性能明显优于包络谱方法。同包络解调一样利用Teager能量谱对信号分析之前,通常采用带通滤波器滤除混杂在信号中的无用成分以提高信噪比[7]。然而,在使用经典带通滤波器对共振带进行提取时,滤波器的通带中心频率及带宽需要取决于操作者的经验去反复尝试,工作量较大[8]。
由于双树复小波包能够将信号非常精细地分解到各个相同带宽的频带内,因此利用双树复小波包对信号进行预处理,能取得比带通滤波器更好的应用效果[9]。双树复小波包在保留双树复小波的抗频带混叠、近似平移不变和完全重构等[10-14]优良性质的同时,对没有分解的高频部分继续分解,从而提高了整个频段的频率分辨率,也减少了特征信息的丢失,是非常理想的机械故障信号预处理方法。
利用双树复小波包对信号进行预处理并没有彻底解决共振带的提取问题,而是转化到最优分解层数确定与频带的选择上。为了从分解后的频带中准确提取共振带,诸多学者进行了深入的研究。文献[15]提出了基于小波包频带熵的共振带提取方法,取得了满意的效果,但该文献没有研究最佳分解层数的确定问题,仅在某一频带上根据频带熵值最小提取共振带,可能导致共振带提取不完全或者将更多非共振带提取为共振带。崔玲丽等研究了基于小波包系数熵值得共振带提取方法,能够有效提取故障信号的共振带,但对于最佳阈值和最优分解层数没有进一步研究,以至阈值与分解层数的选择需不断尝试。文献[16]提出了小波包频带能量的轴承损伤类故障检测方法,实质是依据能量最大原则提取共振带,但能量极易受到强干扰峰值的影响,致使依据能量最大原则提取共振带的方法可能失效。基于此,本文提出频带幅值熵的概念,它是一种新的能够反映共振带的指标。在此基础上,将双树复小波包变换与Teager能量谱结合,提出了双树复小波包自适应Teager能量谱的滚动轴承早期故障诊断方法,仿真和实验分析结果表明该方法对轴承早期的故障信息具有较高的识别能力。
1 基本理论介绍
1.1 双树复小波包变换
双树复小波包变换是Bayram等在离散小波包变换和双树复小波变换的基础上提出的一种改进变换。DT-CWPT弥补了离散小波包变换的方向选择性和平移敏感性缺陷,同时也保留了双树复小波变换的优良特性。
双树复小波包变换的分解与重构实现非常简单,它是由两个相互平行且使用不同的低通和高通滤波器的离散小波包变换构成,可分别看做实部树和虚部树,这样在对输入信号进行分解的过程中能够实现信息互补,也可以减小因平移变换对信号特征提取的影响,该变换对双树复小波没有分解的高频部分继续分解,避免了有效信息的丢失。
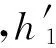
1.2 Teager能量算子与Teager能量谱
Teager能量算子是一种简单的非线性差分算子,用于跟踪与分析窄带信号的能量。对连续时间信号x(t)它的定义为
(1)
对于经DT-CWPT分解后得到的离散信号X(t)而言,可用差分代替上式中的微分,既有:
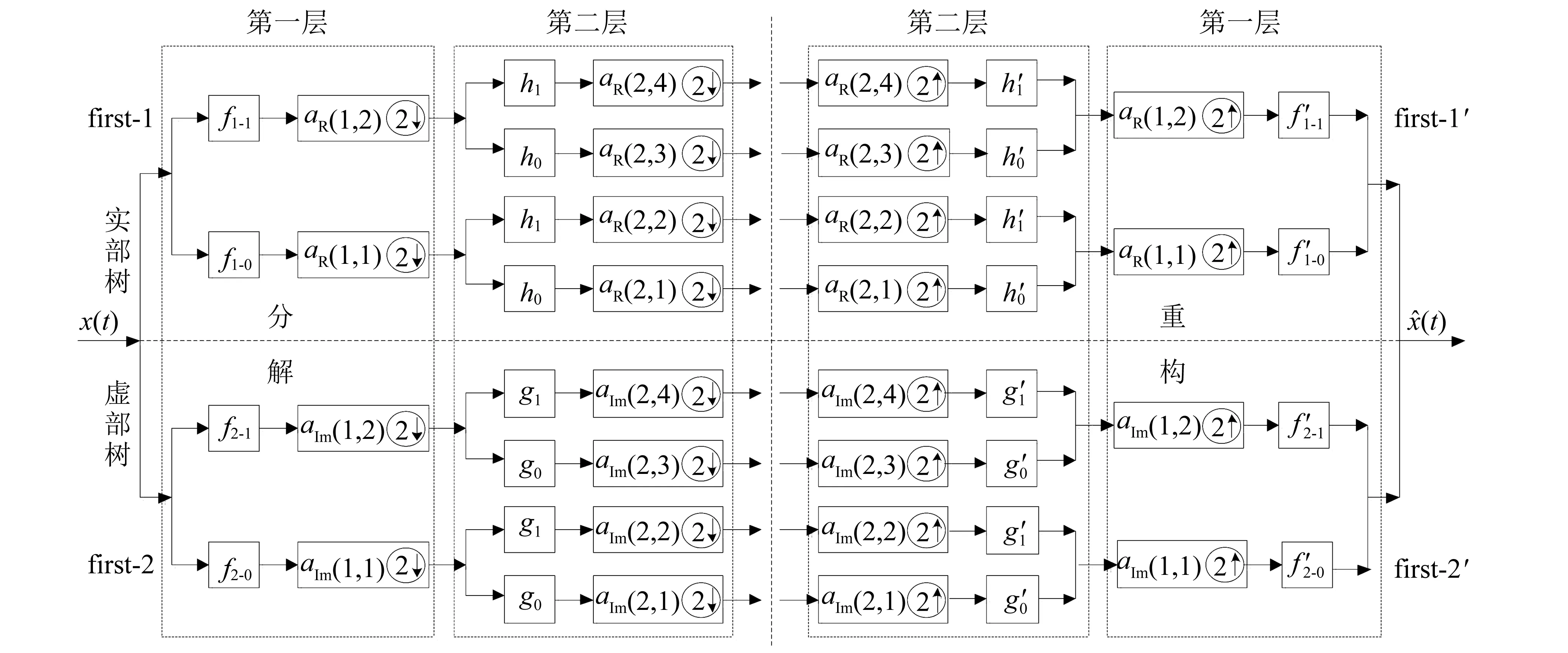
图1 DT-CWPT的分解与重构过程Fig. 1 Decomposition and reconstruction process using dual-tree complex wavelet packet transform
(2)
由式(2)可知,对于离散时间信号,Teager能量算子只需3个样本数据便可计算出信号源在任意时刻的总能量,因此它对于信号的瞬态变化具有较好的时间分辨率和自适应能力,在信号的冲击特征检测方面具有独特优势。Teager能量谱即是基于Teager能量算子这一优势提出的:首先计算信号的Teager能量算子输出,再对输出进行FFT变换,得到Teager能量谱,最后从能量谱中即可准确地识别出轴承故元件的障特征频率。
1.3 频带幅值熵
为从双树复小波包分解后的频带中自适应且有效地提取共振带,本文提出了频带幅值熵的概念,它是一类新的能反映频带内频率成分随时间变化的指标,其定义如下:
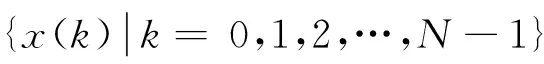
(3)
由于X为频谱幅值矩阵,X的所有元素均大于零,为了让幅值有相同的度量标准,将矩阵的所有元素都归一化到区间[0,1]内。然后将[0,1]划分为M个相等长度的区间:[0,a1],[a1,a2],[a2,a3],...,[aM-1,1]。假设第i个子带系数的频谱幅值落在区间[am-1,am]的点数为Nm,那么该子带系数频谱幅值落在区间[am-1,am]的概率为
(4)
式中:m表示第m个区间;N为每个子空间小波包系数的长度。因此,第i个子带系数的频带幅值熵定义为
(5)
对于滚动轴承故障信号,共振频带上的频率幅值从小到大均有分布,因此幅值归一化后在区间[0,1]会分布的比较均匀,其频带幅值熵较大;共振带以外的频率幅值通常比较小,归一化后在区间[0,1]分布得不均匀,故其频带幅值熵较小。因此,利用频带幅值熵这一指标能够很好地反映出冲击特征,准确地指示出共振带。
1.4 共振带自适应提取算法
峭度是对信号偏离正态分布程度的一个重要衡量指标,归一化的峭度定义为
(6)
式中:K为其峭度;x(n)为去均值后信号;σ为标准差;N为信号长度。峭度对信号幅值变化的表现非常敏感,而这种敏感性主要体现在早期脉冲类故障会导致振动信号峭度明显上升[17]。
基于此,本文提出共振带的自适应提取算法流程如下:
(1)利用双树复小波包将原始信号分解至J层,J的选择一般较大,要保证第J层频带的带宽大于轴承最高故障特征频率的3倍,以保证有效提取故障冲击特性信息。
(2)求出各层各子带的频带幅值熵。
(3)在双树复小波包分解的每一层中,将各子带的频带幅值熵按升序排列后依次作为阈值,提取频带幅值熵大于阈值的子带,并计算每个阈值提取出的子带之和的峭度,峭度最大时所对应的子带之和为从该层子带中选出的共振带,此时的阈值为该层的最优阈值。
(4)计算每层选出的共振带的峭度值并进行比较,选择峭度最大的共振带作为最终提取的共振带,此时对应的层数为双树复小波包最佳分解层数。
2 基于双树复小波包变换自适应Teager能量谱早期故障诊断方法
本文将双树复小波包变换与Teager能量谱,以及提出的共振带自适应提取算法融合,提出基于基于双树复小波包变换自适应Teager能量谱早期故障诊断方法,其基本流程如图2所示。
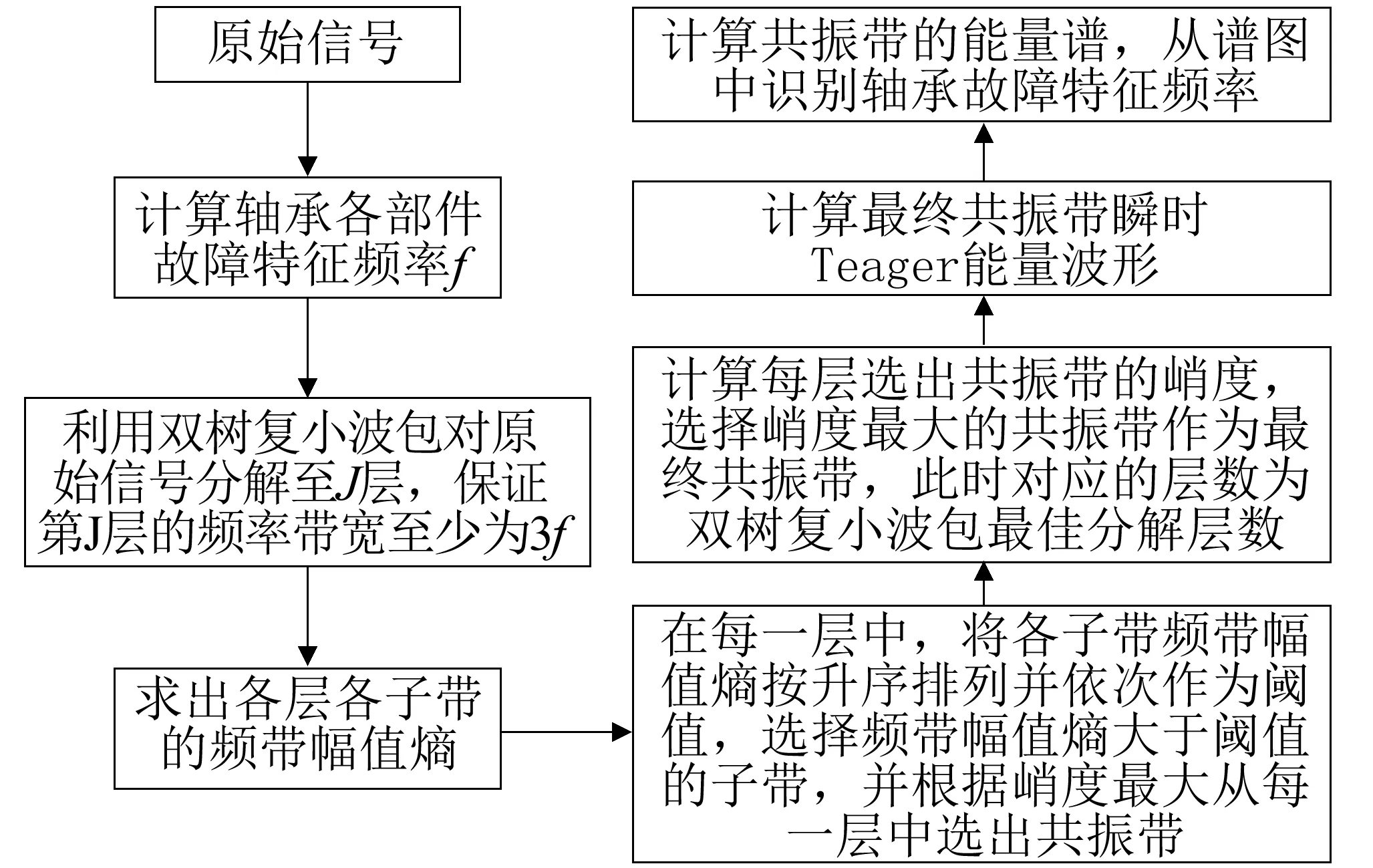
图2 早期故障诊断方法流程图Fig. 2 Flow chart of early fault diagnosis method
3 仿真信号分析
根据轴承外圈故障产生的机理及其振动数学模型[18-19],构造单一调制源两个载波中心且包含强噪声的滚动轴承外圈故障振动响应信号如下:
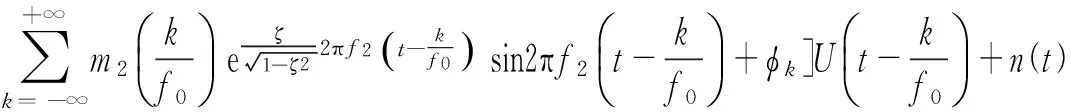
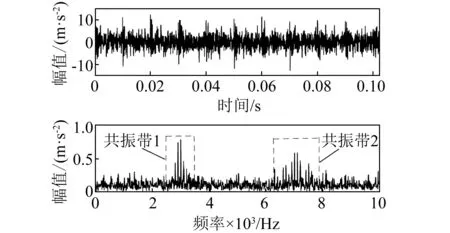
图3 外圈故障仿真信号及其频谱Fig.3 Fault simulation signal of bearing outer ring and its frequency spectrum
由于仿真信号中设置的外圈故障特征频率f0=100 Hz,其3倍频为300 Hz,故最大分解层数为4较为合适。首先对采样信号利用双树复小波包变换分解至第4层,并求出各层各子带的频带幅值熵。然后根据本文提出的算法,依次从双树复小波包分解后的每一层中提取的共振带如图4所示。再计算每层选出的共振带峭度如图5所示。从图5中可以看到,第3层提取出的共振带峭度值最大,故双树复小波包最佳分解层数为3,最终得到的共振带为第3层提取的共振带。
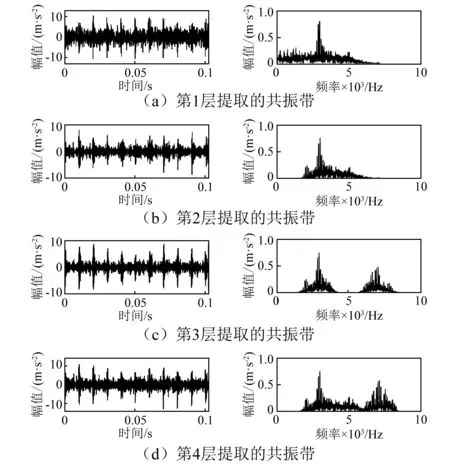
图4 各层提取的共振带Fig.4 Each layer extraction of the resonance band
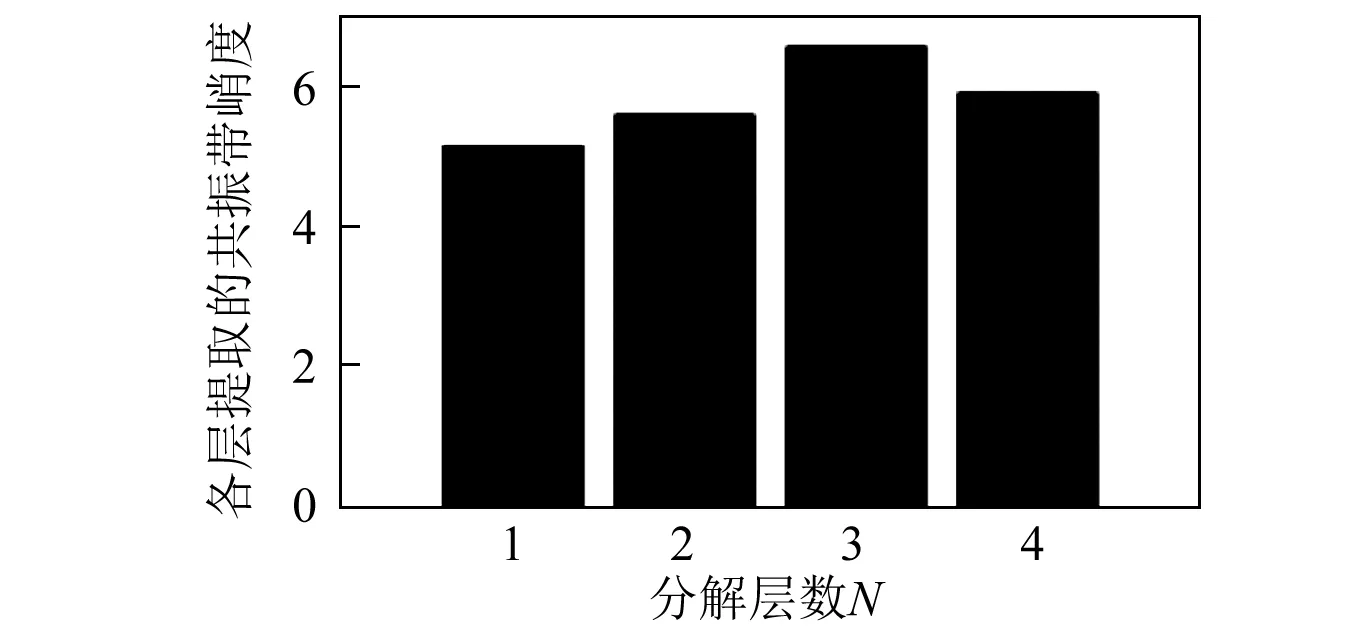
图5 各层提取的共振带峭度Fig.5 Kurtosis value of each resonance band
为验证第3层提取的共振带确实是最优的,本文对图4中各层提取出的共振带进行比较。由图4可知,第1、2层只提取到了一处共振带,并且将一些噪声成分提取为共振带,第4层虽然将两处的共振带都提取到,但同时也将更多的噪声带入了共振带;只有第3层恰好将两处的共振带都提取出来且又不含多余频带,实现了共振带与噪声的最佳分离。
图6所示为第3层各子带的频带幅值熵。将第3层各子带的频带幅值熵按升序排列后依次作为阈值提取频带幅值熵大于或等于阈值的频带。每个阈值提取的频带峭度值如图7所示。由图6和图7可知,峭度最大的频带是处于次大位置的频带幅值熵0.652 8作为阈值提取的频带,该频带是由第3层序号为3和6的子带构成,即第3层提取的共振带如图4(c)所示,此时该阈值为第3层的最佳阈值。
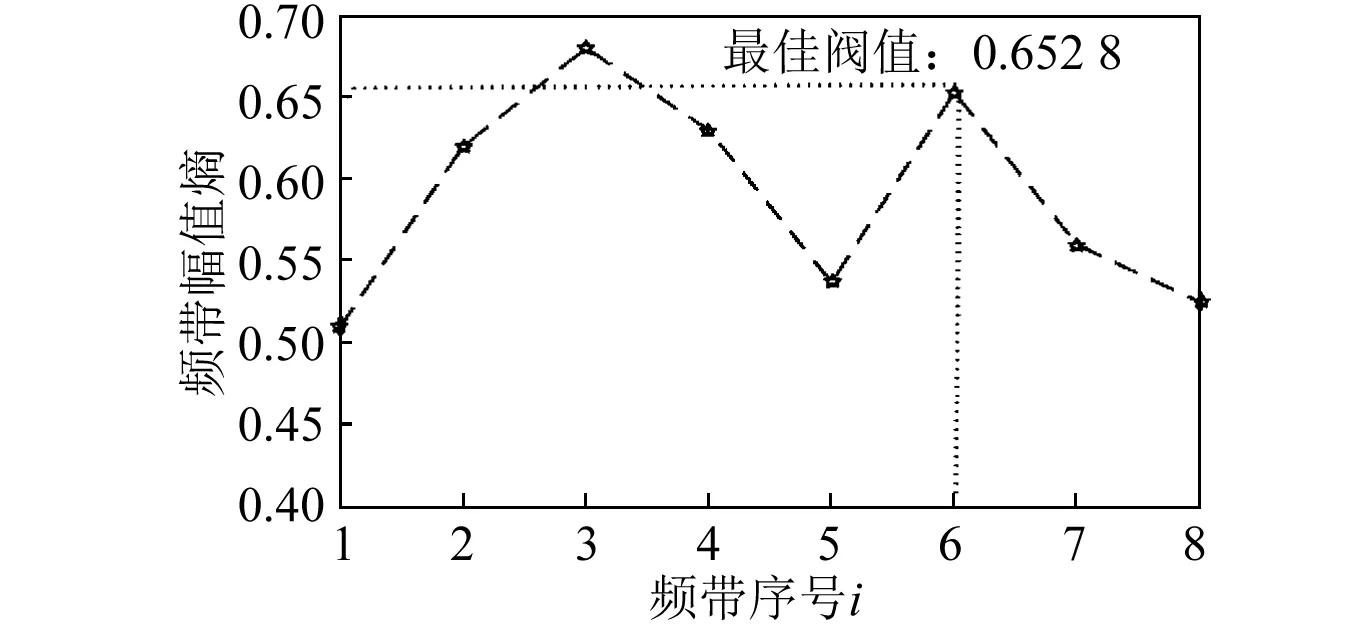
图6 第3层各子带的频带幅值熵Fig.6 Frequency band amplitude entropy of each sub band in the third layer
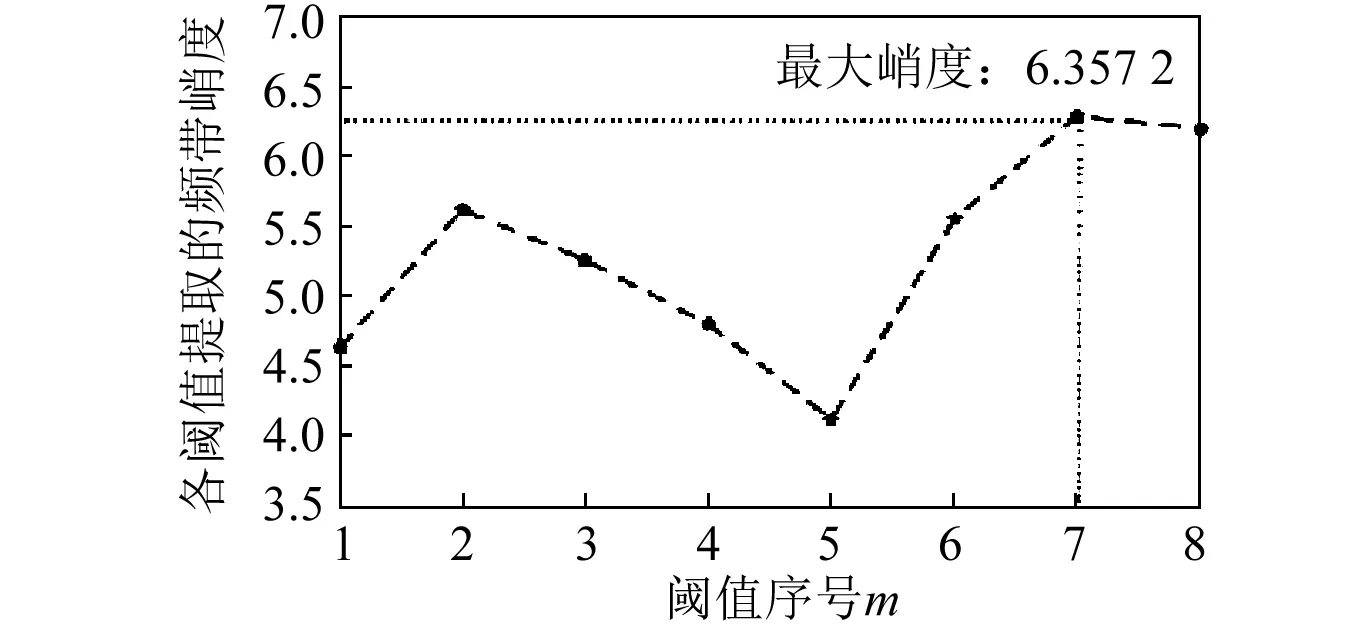
图7 第3层各子带的阈值提取的频带峭度值Fig.7 The kurtosis value obtained from the frequency threshold of each sub band in the third layer
将Teager能量算子作用于第3层提取的共振带,得到共振带的瞬时能量波形如图8(a)所示。从图中可以看到,瞬时能量波形出现了间隔约为0.001 s的等间隔冲击。图8(b)所示为共振带的Teager能量谱,谱图中清楚地显示出最大谱峰对应的频率为100 Hz,其次为200 Hz,300 Hz,400 Hz等峰值分别与其倍频相对应,故从Teager能量谱中成功地提取到了外圈故障特征频率信息。
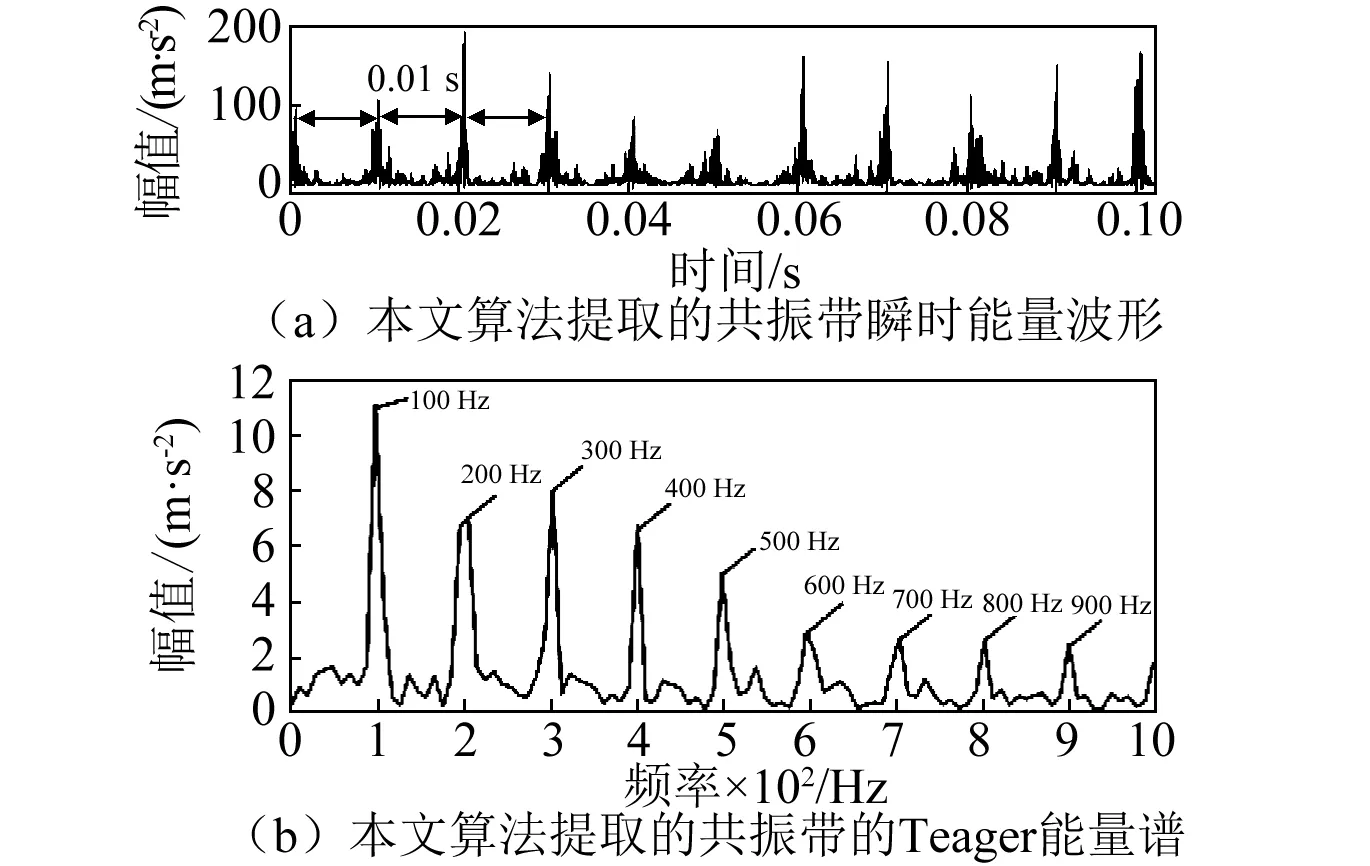
图8 仿真信号共振带瞬时能量波形及其Teager能量谱Fig.8 Instantaneous energy waveform and Teager energy spectrum of he resonance band in the simulation signal
作为对比,本文采用带通滤波的方法(以仿真信号设定轴承元件的固有频率f1,f2分别为中心频率,带宽都为1 000 Hz)提取仿真信号的共振带,再对所提取的共振带进行包络分析。图9为该方法提取出的共振带的包络及包络谱。由图9(a)可知,包络波形中含有较多的噪声,并且包络的等间隔冲击特征不如图8(a)中本文算法提取出的共振带瞬时能量波形的等间隔冲击特征突出。由图9(b)可知,图中包络谱尽管也能提取到故障特征频率信息,但是可以看出其频谱中存在许多其他频率成分,不如图8(b)中的Teager能量谱清晰。可见,本文所提方法能更加有效地提取轴承的故障特征频率信息。
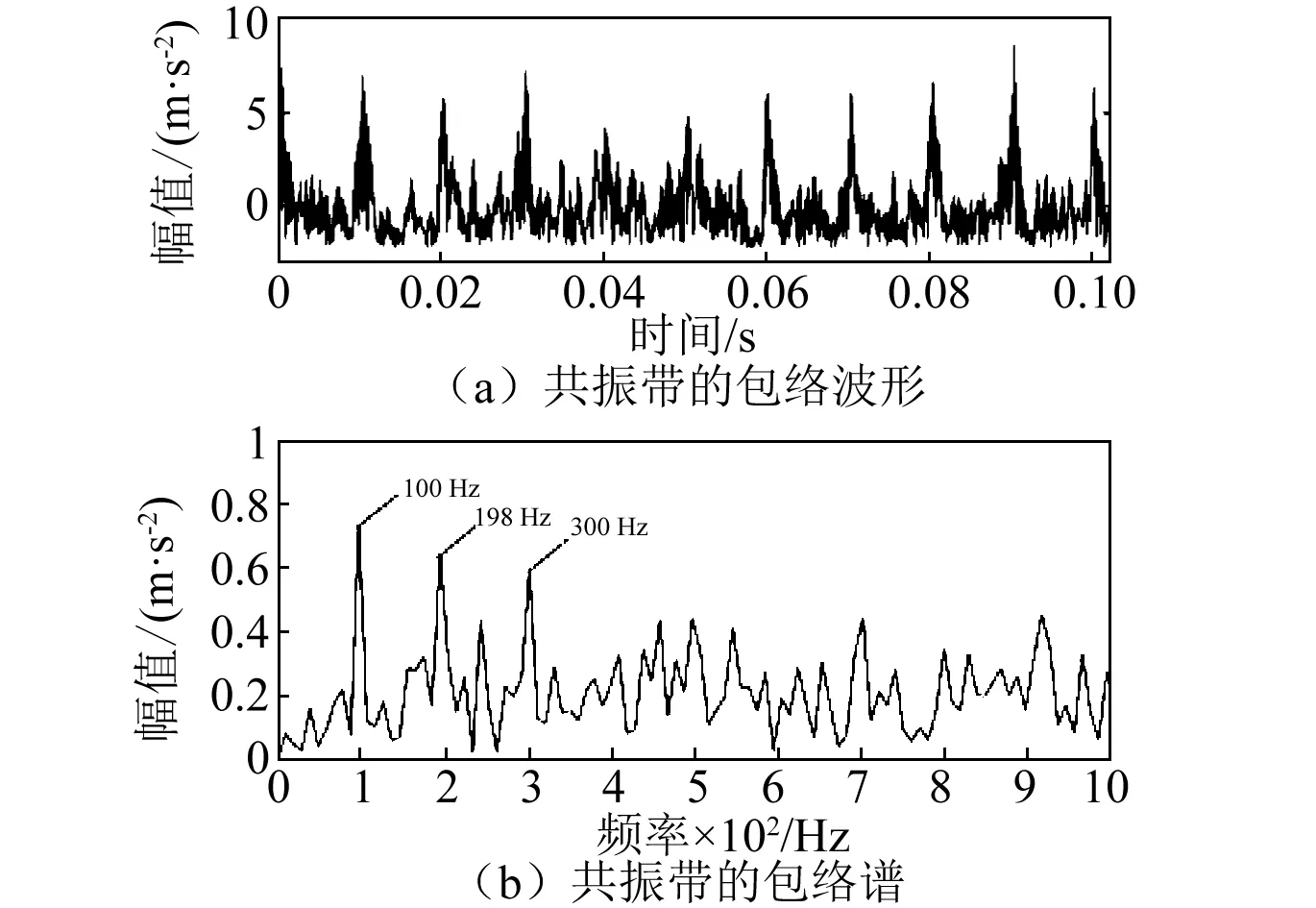
图9 仿真信号共振带包络及其包络谱Fig.9 The envelope and envelope spectrum of the resonance band in the simulation signal
4 实验案例分析
滚动轴承的故障数据来源于美国Case Western Reserve大学电气工程实验室的滚动轴承故障模拟实验台,如图 10所示。该实验台由电动机(图10左)、联轴器、扭转传感器(图10中)、功率测试计(图10右)、调速系统和数据采集系统组成。加速度传感器安装在电动机驱动端与风扇端轴承的轴承座垂直方向位置以及电机支撑底盘上。
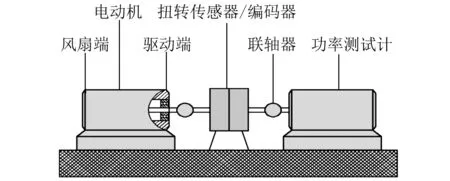
图10 故障模拟实验台Fig.10 Bearing fault test rig
实验时,驱动端的轴承型号为SKF6205-2RS JEM,风扇端的轴承型号为SKF6203-2RS JEM,其尺寸信息如表 1所示。实验通过点火花加工的方式分别在驱动端和风扇端轴承的内圈、外圈、滚动体上制造点蚀故障,故障尺寸设置分别为:0.177 8,0.355 6,0.533 4 mm。
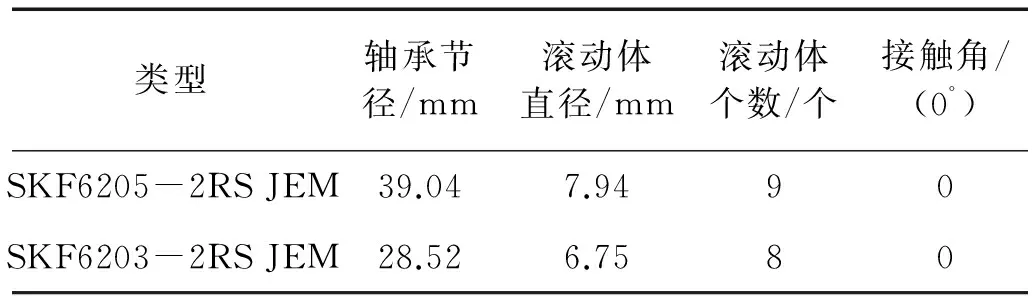
表1 驱动端和风扇端轴承尺寸信息
4.1 外圈早期故障特征提取
实验选用驱动端6205深沟球轴承,轴承的内圈保持完好,外圈在负载方向存在早期损伤故障(损伤直径:0.18 mm,损伤深度:0.28 mm)。实验设定采样频率为12 kHz,所用数据长度为2 048点,电机转速为1 797 r/min (对应的旋转频率fr为29.95 Hz),此时轴承外圈故障特征频率fout为107.4 Hz。
轴承外圈损伤时测取的振动数据时域波形及其频谱如图11(a)所示。由图11(a)可知,时域信号中含有噪声成分较少,冲击特征非常明显,而且在频域中外圈故障激起的共振带清晰可见,频率范围为[2.5,3.5]kHz。为验证本文提出的共振带自适应提取算法在强噪声中的有效性,本文在原始信号中特意加入强噪声,加入噪声后的信号及其频谱如图11(b)所示。从图11(b)中可以看到,时域信号中冲击特征已被噪声掩盖,频域内的共振带也有很多部分淹没在噪声中。
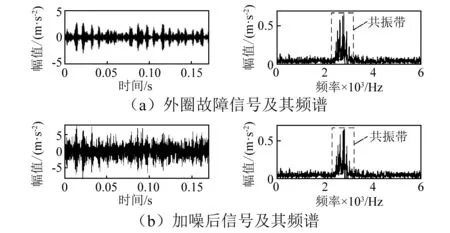
图11 外圈早期故障波形及其频谱Fig.11 Waveform and spectrum of the early fault of outer ring
因轴承的最大特征频率为内圈故障特征频率162.2 Hz,其3倍频为486.6 Hz,故最大分解层数为3较为合适。利用双树复小波包变换对采样信号分解至第3层,并求出各层各子带的频带幅值熵。然后根据本文提出的算法,依次从每一层中提取共振带,再计算每层选出的共振带峭度如图12所示。从图12中可以看到,第3层提取出的共振带峭度值最大,故双树复小波包最佳分解层数为3,最终得到的共振带为第3层提取的共振带。图13为各层提取到的共振带,从图中能够清晰地看到第3层提取的共振带的确为各层提取结果的最优,第1、2层尽管都提取到了共振带,但同时也将更多噪声带入了共振带,没有达到最佳的分离效果。
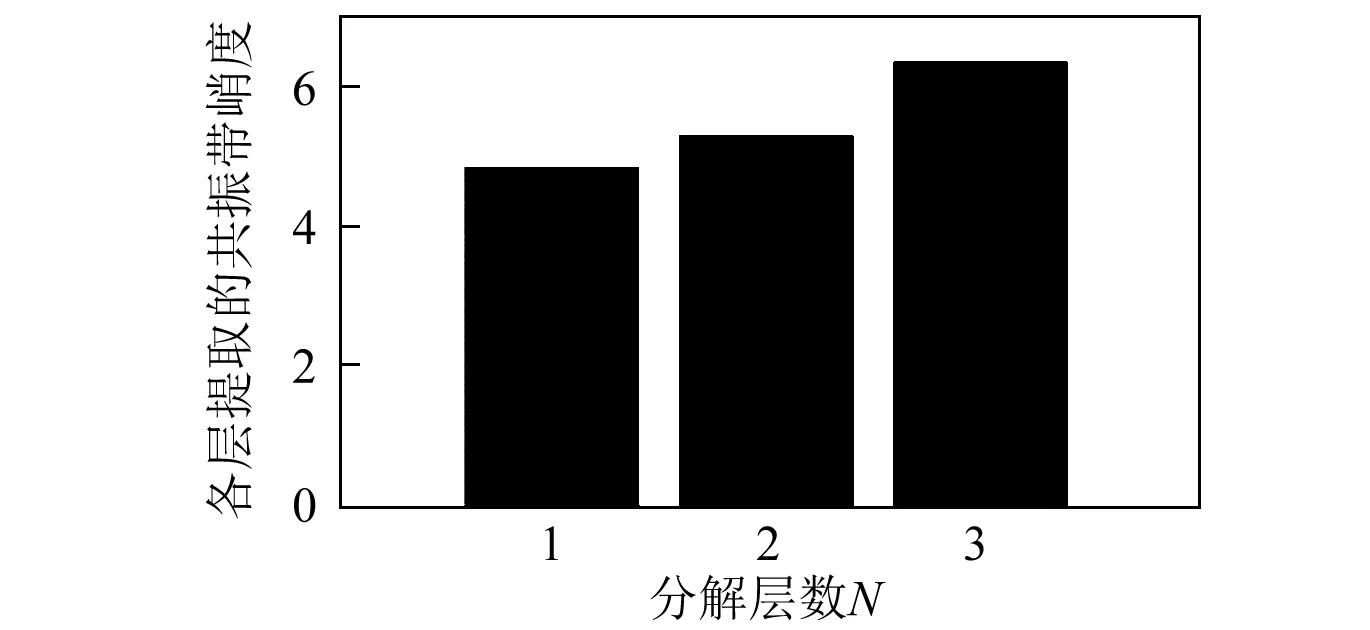
图12 各层提取的共振带峭度Fig.12 Kurtosis value of each resonance band
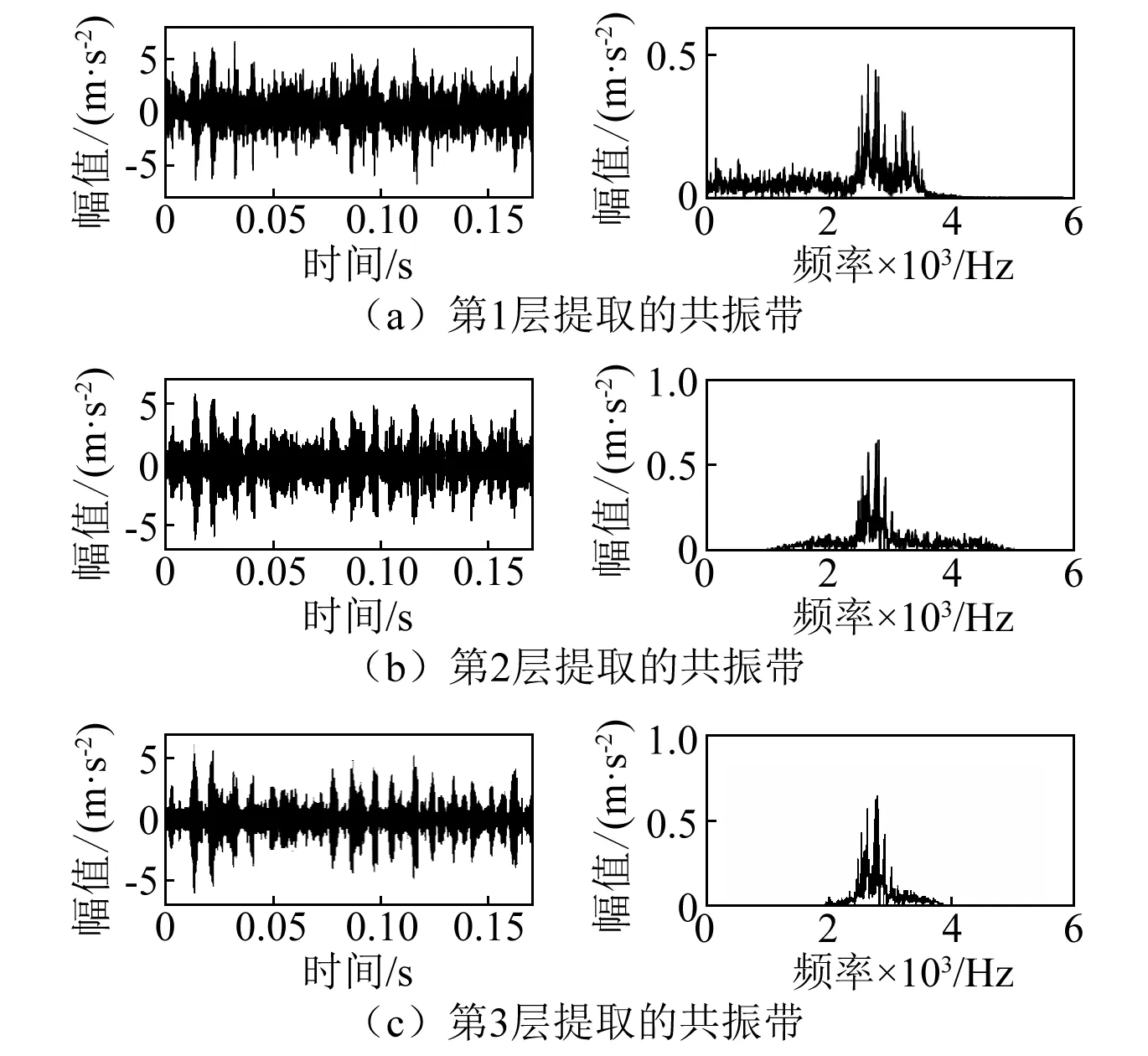
图13 各层提取的共振带Fig.13 Each layer extraction of the resonance band
图14为第3层各子带的频带幅值熵,将第3层各子带的频带幅值熵按升序排列,并依次作为阈值提取熵值大于或等于阈值的频带。图15为每个阈值提取的频带峭度值。由图14和图15可知,峭度最大的频带位于次大位置的熵值0.875 2作为阈值提取的频带,该频带由第3层序号为4和5的子带组成,即第3层提取的共振带如图12(c)所示。
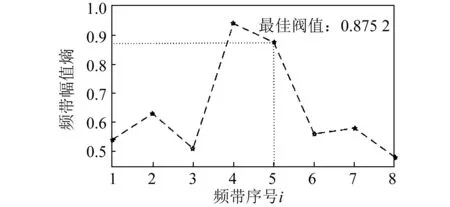
图14 第3层各子带的频带幅值熵Fig.14 Frequency band amplitude entropy of each sub band in the third layer
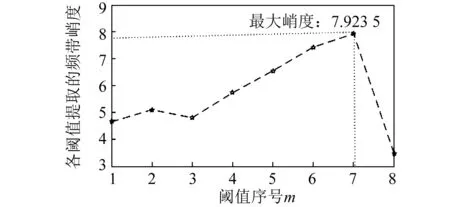
图15 第3层各子带的阈值提取的频带峭度值Fig.15 The kurtosis value obtained from the frequency threshold of each sub band in the third layer
图16(a)为本文算法提取出共振带的瞬时能量波形,从图中能够清晰地看到瞬时能量波形中出现了间隔约为9.3 ms的等间隔冲击。对瞬时能量波形求频谱得到如图16(b)所示的Teager能量谱,谱图中在107 Hz及2、3、4倍频处出现了明显的峰值。至此,基于双树复小包变换自适应Teager能量谱早期故障诊断方法非常成功地提取到外圈故障特征频率,实现了外圈早期故障的自适应精确诊断。
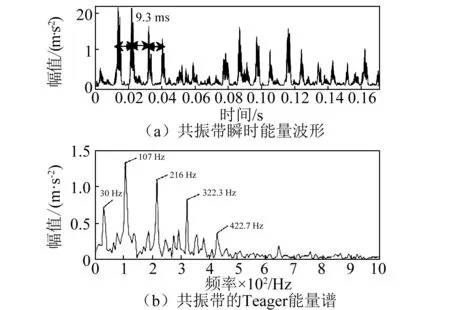
图16 外圈故障信号共振带瞬时能量波形及其Teager能量谱Fig.16 Instantaneous energy waveform and Teager energy spectrum of bearing outer ring fault signal
作为比较,采用带通滤波的方法(根据共振带的频响范围设定中心频率为3 000 Hz,带宽为500 Hz)提取轴承外圈故障振动信号的共振带,图17为该方法提取出的共振带的包络及包络谱。由图17(a)可知,图中的包络受噪声干扰,等间隔冲击特征不如图16(a)中瞬时能量波形的等间隔冲击特征清晰。由图17(b)可知,在包络谱中峰值频率与故障特征频率及其倍频能够相互对应,但是频谱的峰值没有图16中的效果突出,而且提取出来的最高阶频率成分仅为2阶。因此,本文所提的方法能够更加有效地提取滚动轴承外圈的故障特征信息。
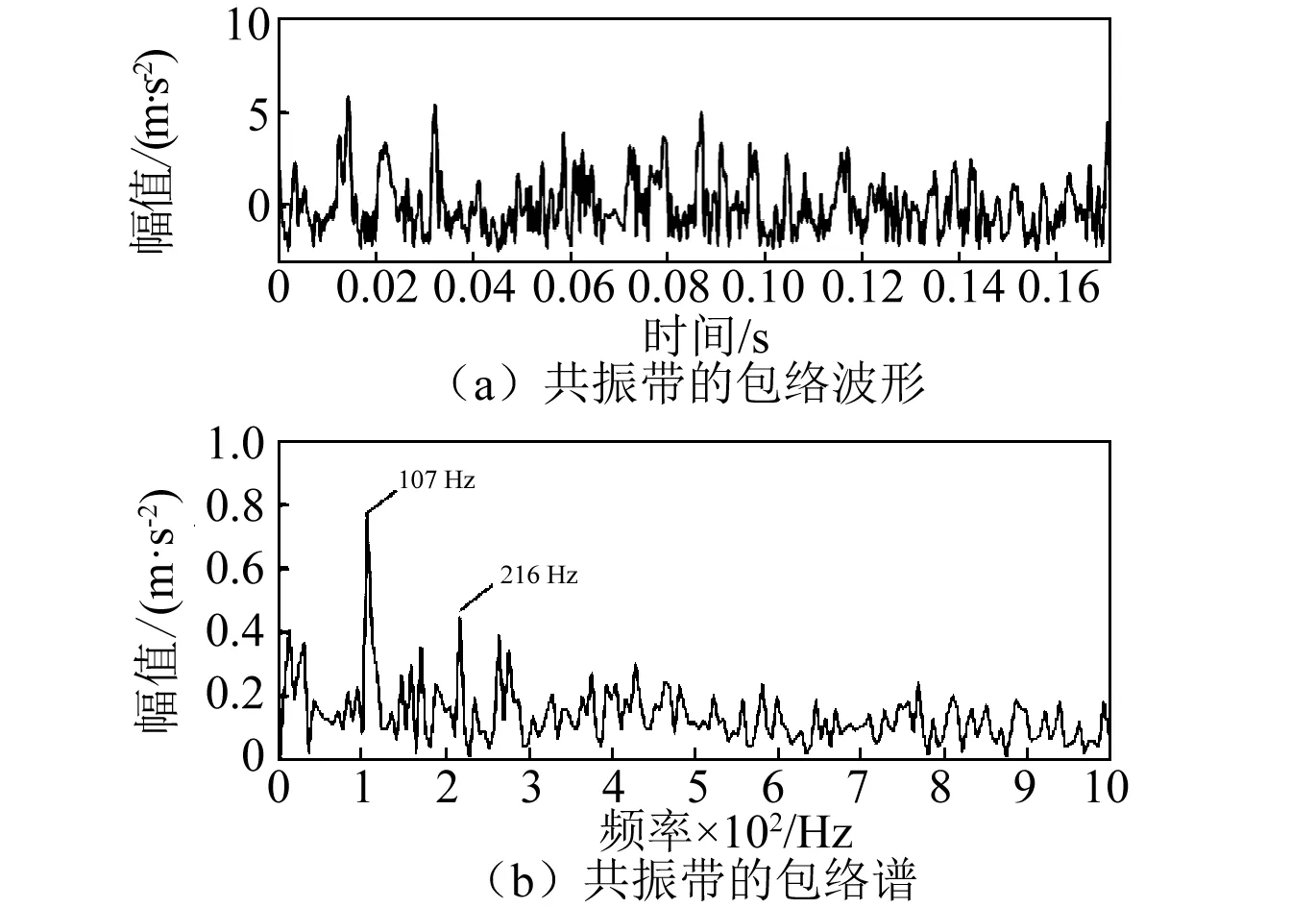
图17 外圈故障信号共振带包络及其包络谱Fig.17 The envelope and envelope spectrum of resonance band of bearing outer ring fault signal
4.2 内圈早期故障特征提取
实验选用风扇端6203深沟球轴承,轴承的外圈保持完好,内圈存在早期损伤故障(损伤直径:0.18 mm,损伤深度:0.28 mm)。对该信号进行采集时,采样频率设置为12 kHz,所用数据长度为2 048点,电机转速为1 797 r/min(对应的旋转频率为29.95 Hz)此时内圈故障特征频率finner为148.2 Hz。
轴承内圈损伤时测得的振动信号时域波形及其频谱如图18所示。由图18可以看到,时域信号中出现了与转频相对应的等间隔冲击,但与内圈故障频率对应的冲击没有出现;在频域中外圈故障激起了2处共振带,频率范围分别为[1,2]kHz和[3,4]kHz。
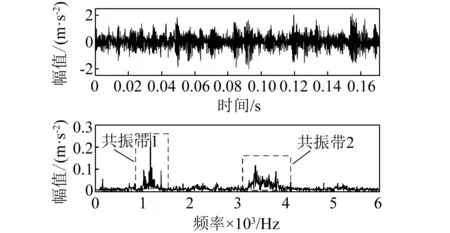
图18 内圈早期故障波形及其频谱Fig.18 Waveform and spectrum of the early fault of inner ring
由于轴承的最大特征频率为内圈故障特征频率finner=148.2 Hz,其3倍频为444.6 Hz,故最大分解层数为3较为合适。对采样信号利用双树复小波包变换分解至第3层,并求出各层各子带的频带幅值熵。然后根据本文提出的算法,依次从每一层中提取共振带,再计算每层选出的共振带峭度如图19所示。从图19中可以看到,第3层提取出的共振带峭度值最大,故双树复小波包最佳分解层数为3,最终得到的共振带为第3层提取的共振带如图20所示。由图20可知,本文算法将故障激起的2处共振带从含噪声的原始信号频谱中成功地分离出来,非常有利于共振带内特征的提取与分析。
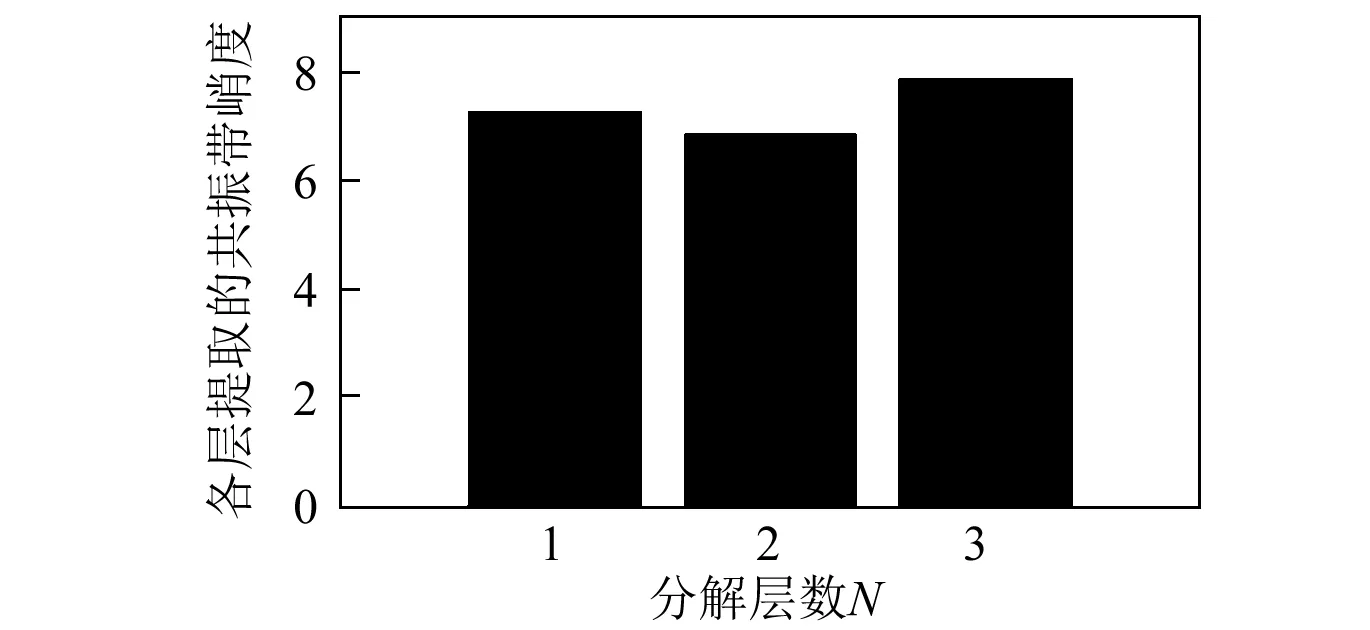
图19 各层提取的共振带峭度Fig.19 Kurtosis value of each resonance band
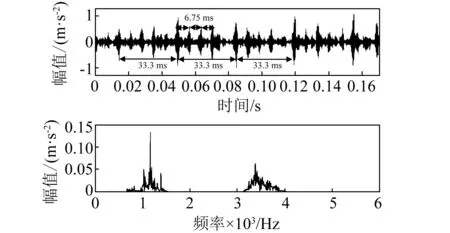
图20 第3层提取的共振带Fig.20 Third layer extraction of the resonance band
将Teager能量算子作用于提取出的共振带,得到共振带的瞬时能量波形如图21(a)所示。从图中可以看到,瞬时能量波形出现了间隔约为6.75 ms的等间隔冲击。对瞬时能量波形求频谱得到如图21(b)所示的Teager能量谱,谱图中在转频的2倍频处、内圈故障特征频率148 Hz及其倍频处出现了明显的峰值,而且在两侧出现了间隔为60 Hz的边频带,至此,基于双树复小包变换自适应Teager能量谱早期故障诊断方法非常成功地实现了内圈早期故障的自适应精确诊断。
作为比较,采用带通滤波的方法(根据共振带的频响范围设置中心频率分别为1 500 Hz与3 500 Hz,带宽均为500 Hz)提取轴承外圈故障振动信号的共振带,图22为该方法提取出的共振带的包络以及包络谱。由图22可知,图中包络的等间隔冲击特征以及包络谱中的故障特征频率、边频带特征,都明显不如图21中的清晰。因此,本文所提的方法能够更加有效地提取滚动轴承内圈的故障特征信息。
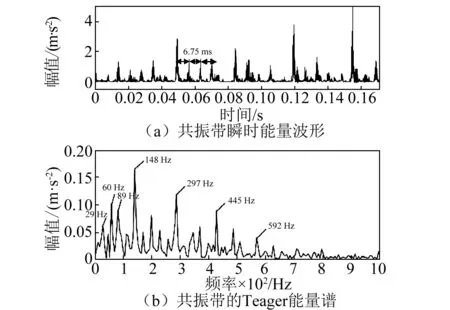
图21 内圈故障信号共振带瞬时能量波形及其Teager能量谱Fig.21 Instantaneous energy waveform and Teager energy spectrum of bearing inner ring fault signal
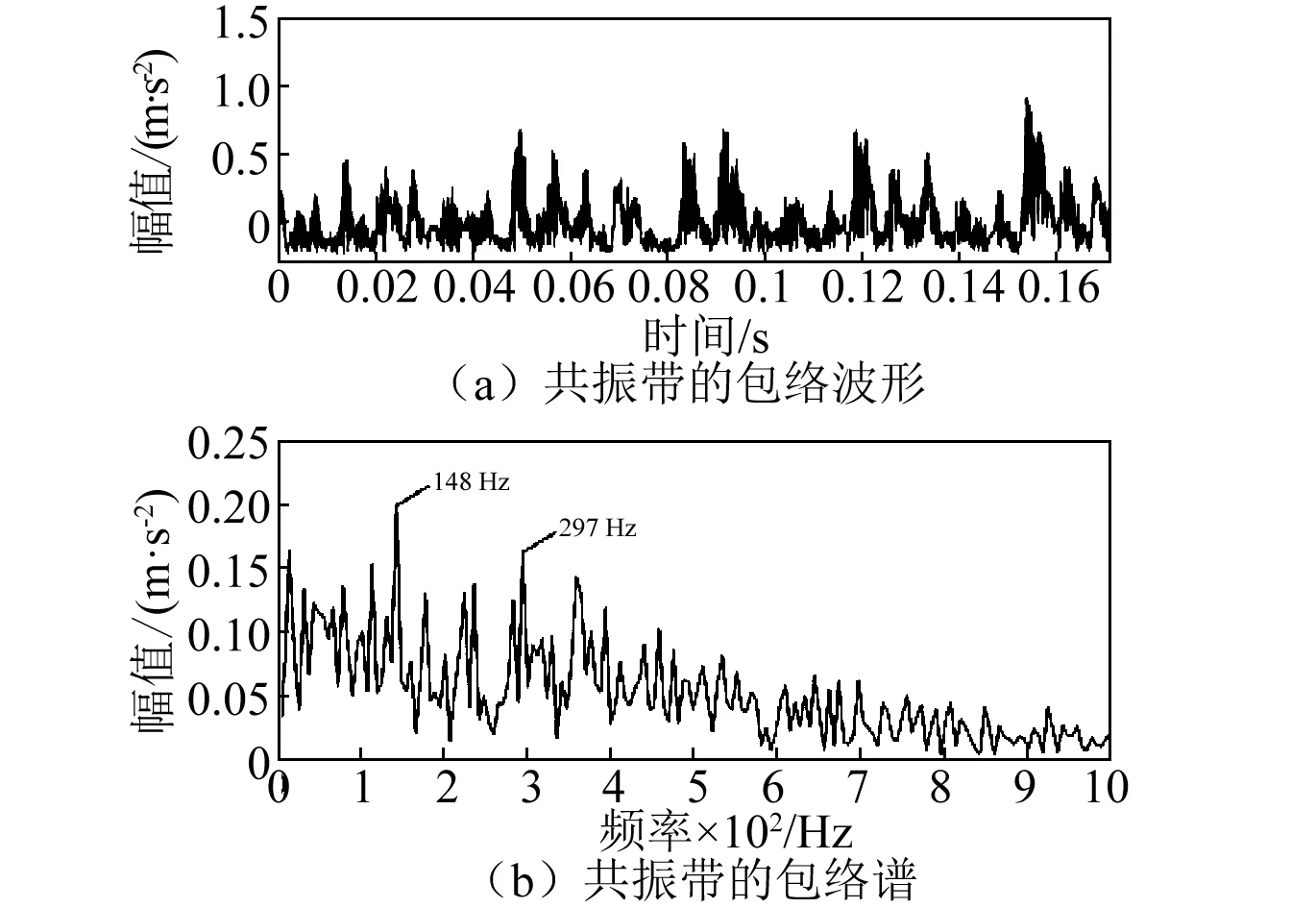
图22 内圈故障信号共振带包络及其包络谱Fig.22 The envelope and envelope spectrum of resonance band of bearing inner ring fault signal
5 结 论
本文研究了基于双树复小包变换自适应Teager能量谱早期故障诊断方法,通过对仿真信号和实验案列的分析结果可知,该方法非常有利于共振带内故障特征的提取,在滚动轴承早期类故障诊断中具有明显的优势。
(1)本文提出的自适应共振带提取方法,能够将故障冲击激起的共振带从包含强噪声的原始信号的频谱中准确地分离出来,几乎可以达到自动执行,最大限度地减少了人为因素的影响。
(2)在微弱的轴承早期冲击性故障检测与识别轴承故障特征频率方面,本文所提出的诊断方法比传统的共振频带包络分析法更加有效。
(3)基于双树复小波包变换自适应Teager能量谱早期故障诊断方法,能够保证滚动轴承的早期微弱故障特征提取的准确性与故障诊断的可靠性,在实际工程应用中具有较大的潜力。
[1] WANG Yi , XU Guanghua , LIANG Lin, et al. Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2015,54: 259-276.
[2] 何正嘉,袁静,訾艳阳.机械故障诊断的内积变换原理与应用[M].北京:科学出版社,2011.
[3] 崔玲丽,康晨辉,张建宇,等.基于时延相关及小波包系数熵阈值的增强型共振解调方法[J].机械工程学报,2010,46(20):53-57. CUI Lingli, KANG Chenhui, ZHANG Jianyu, et al. Enhanced resonance demodulation based on the delayed correlation and entropy threshold of wavelet packet coefficients[J]. Chinese Journal of Mechanical Engineering, 2010,46(20):53-57.
[4] 田福庆,罗荣,贾兰俊,等.机械故障非平稳特征提取方法及其应用[M].北京:国防工业出版社,2014.
[5] 张进,冯志鹏,褚福磊.滚动轴承故障特征的时间-小波能量谱提取方法[J].机械工程学报,2011,47(17):44-49. ZHANG Jin , FENG Zhipeng ,CHU Fulei . Extraction of rolling bearing fault feature based on time-wavelet energy spectrum [J]. Chinese Journal of Mechanical Engineering, 2011,47(17):44-49.
[6] 王天金,冯志鹏,郝如江,等.基于Teager能量算子的滚动轴承故障诊断研究[J].振动与冲击,2012,31(2):1-5. WANG Tianjin,FENG Zhipeng,HAO Rujiang,et al. Fault diagnosis of rolling element bearings based on Teager energy operator[J]. Journal of Vibration and Shock,2012,31(2):1-5.
[7] CHENG Junsheng, YU Dejie, YANG Yu. The application of energy operator demodulation approach based on EMD in machinery fault diagnosis[J].Mechanical Systems and Signal Processing, 2007, 47 (6):1011-1020.
[8] 周智,朱永生,张优云,等.基于EEMD和共振解调的滚动轴承自适应故障诊断[J].振动与冲击,2013,32(2):76-80. ZHOU Zhi, ZHU Yongsheng, ZHANG Youyun, et al. Adaptive fault diagnosis of rolling bearings based on EEMD and demodulated resonance[J].Journal of Vibration and Shock,2013,32(2):76-80.
[9] BAYRAM I, SELESNICK I W. On the dual-tree complex wavelet packet transform and M-Band transforms[J].IEEE Transactions on Signal processing,2008,56(6):2298-2310.
[10] WANG Yanxue, HE Zhengjia, ZI Yanyang. Enhancement of signal denoising and multiple fault signatures detecting in rotating machinery using dual-ture complex wavelet transform[J].Mechanical system and signal processing,2010,24(1):119-137.
[11] SELESNICK I W, BARANIUK R G, KINGSBURY N G. The dual-tree complex wavelet transform [J].IEEE Digital Signal Processing Magazine, 2005, 22(6):123-151.
[12] 李辉,郑海起,唐力伟.基于双树复小波包峭度图的轴承故障诊断研究[J].振动与冲击,2010,31(10):13-18. LI Hui, ZHENG Haiqi, TANG Liwei. Bearing fault diagnosis based on kurtogram of dual-tree complex wavelet packet transform[J]. Journal of Vibration and Shock, 2010,31(10):13-18.
[13] 胥永刚,孟志鹏,陆明.基于双树复小波包变换的滚动轴承故障诊断[J].农业工程学报,2013,29(10):49-56. XU Yonggang, MENG Zhipeng, LU Ming. Fault diagnosis of rolling bearing based on dual-tree complex wavelet packet transform[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(10):49-56.
[14] KINGSBURY N. Design of Q-shift complex wavelets for Image processing using frequency domain energy minimisation [C]//Proceedings of the IEEE Conference on Image Processing. Barcelona, 2003: 1013-1016.
[15] 王小玲,陈进.丛飞云.基于时频的频带熵方法在滚动轴承故障识别中的应用[J].振动与冲击,2011,31(18):29-33. WANG Xiaoling, CHEN Jin, CONG Feiyun. Application of spectral band entropy (SBE) method in rolling bearing fault diagnosis based on time-frequency analysis[J]. Journal of Vibration and Shock,2011,31(18):29-33.
[16] 段晨东,郭研.基于提升小波包变换的滚动轴承包络分析诊断方法[J].农业机械学报,2007,39(5):192-196. DUAN Chendong, GUO Yan. An envelop analysis approach for ball bearing based on lifting wavelet packet transform[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007,39(5):192-196.
[17] XIANG Yong. A further study of the kurtosis-based method for bearing diagnostics[J].Mechanical Systems and Signal Processing,2007,21(1):593-595.
[18] ANTONI J, BONNARDOT F, RAAD A, et al. Cyclostationary modeling of rotating machine vibration signals [J]. Mechanical Systems and Signal Processing, 2004, 18(16):1285-1314.
[19] SAWALHI N, RANDALL R B. Vibration response of spalled roll-ing element bearings: observations, simulations and signal Processing techniques to track the spall size[J].Mechanical Systems and Signal Processing , 2011, 25:846-870.
Incipient fault diagnosis of rolling bearings based on dual-tree complex wavelet packet transform adaptive Teager energy spectrum
REN Xueping, WANG Chaoge, ZHANG Yuhao, WANG Jianguo
(Institute of Mechanical Engineering, Inner Mongolia University of Science and Technology, Baotou 014010, China)
In view of that the incipient fault feature informations of rolling bearings are difficult to identify, and the parameters setting of band-pass filter depends on the user’s experience, which makes the resonance frequency band can’t be effectively determined and extracted, the concept of amplitude entropy of frequency band was introduced. Combining the techniques of wavelet transform and Teager energy spectrum, a rolling bearing incipient fault feature extraction method was proposed and named as the method of dual-tree complex wavelet packet transform adaptive Teager energy spectrum. Original fault signals were decomposed into several different frequency components through wavelet packet transform, and the amplitude entropy of each frequency sub-band was calculated. Then the entropies were arranged in ascending order and in turn were adopted as a threshold to extract the sub bands with the entropy values greater than the threshold values. Based on the kurtosis index, the optimal threshold and the best dual tree complex wavelet packet decomposition levels were determined, thus, the resonance band was extracted adaptively and effectively. Finally, the Teager energy spectrum analysis of the resonance band was performed to identify the frequency of the bearing fault. Through the signal simulation and engineering experiment data analysis, the effectiveness of the proposed method was verified.
amplitude entropy of frequency band; the dual-tree complex wavelet packet transform; Teager energy spectrum; the adaptive resonance frequency band extraction; bearing fault;
国网公司科技项目(GC71-14-006)
2016-01-26 修改稿收到日期: 2016-03-27
任学平 男,博士,教授,1963年5月生
王朝阁 男,硕士生,1992年6月生
E-mail:wangchaoge1992@163.com
TH165;TH133.3;TP206
A
10.13465/j.cnki.jvs.2017.10.014

