钢筋纤维混凝土侵彻深度计算方法研究

孙 蓓， 林志翔, 焦楚杰

(1.广州大学 土木工程学院，广州 510006；2.中国建筑材料科学研究总院，绿色建筑材料国家重点实验室，北京 100024)

钢筋纤维混凝土侵彻深度计算方法研究

孙 蓓1， 林志翔2, 焦楚杰1

(1.广州大学 土木工程学院，广州 510006；2.中国建筑材料科学研究总院，绿色建筑材料国家重点实验室，北京 100024)

应用较为广泛的侵彻经验、半经验公式对普通混凝土和高硬度钢纤维混凝土抗侵彻性能进行了评估，分析了公式的应用范围与局限性，为此将骨料硬度和钢纤维混凝土韧度引入到侵彻深度的计算公式，在试验基础上提出了修正ACE(The Army Corps of Engineers)公式。修正公式计算结果与实际测定结果符合良好，证明了该公式的合理性。

钢纤维混凝土；硬度；韧度；侵彻

随着科学技术的高速发展，高新技术武器钻地弹的威力增长十分迅速，研制和开发抗钻地弹攻击的军事防御材料已经成为世界各国研究的热点，其中钢纤维混凝土被认为是国防建设中具有广泛应用前景的一种新型抗钻地武器材料[1]。尽管目前应用于计算武器侵彻混凝土材料的经验公式有20多种，但可以用于计算侵彻钢纤维混凝土的经验公式却很少，而考虑到骨料硬度的经验公式更是没有。

本文选取各国防护工程研究应用较为广泛且精度较高的五种侵彻经验和半经验公式，简称侵彻公式：BLZ、ACE、Young、SAPL和修正 “BLZ”公式，通过对不同接触速度下钻地弹侵彻普通混凝土和高硬度骨料的钢纤维混凝土(简称高硬度钢纤维混凝土)侵彻深度的评估，分析了各侵彻公式的应用范围与局限性，引入骨料硬度和钢纤维混凝土材料韧度对原有的ACE公式进行修正，得到侵彻深度与靶材性能的近似计算公式，为抗钻地武器材料的设计提供有效的数据依据。

1 现有侵彻经验、半经验公式的评估

1.1 评估用经验和半经验公式

各国防护工程研究应用较为广泛且精度较高的五种评估用侵彻公式[2-5]。

(1)BLZ(别列赞)公式：1912年由俄国提出，适应于土壤、混凝土、砂岩等地质材料侵彻深度的计算。

Lmax=λ1λ2Kqm/d2×vccosα

(1)

式中：Lmax为侵彻深度(m)，λ1、λ2为分别为弹形系数、弹径系数，在此分别选取1.3和1.3，Kq为介质材料侵彻系数，m为弹重(质量)(kg)，d为弹径(m)，vc为接触速度(m/s)，α为命中角(°)，即弹的轴线与目标表面法线的夹角，fc为混凝土无侧限抗压强度(MPa)。

(2)ACE (The Army Corps of Engineers)公式：1946年美国陆军工程兵用37 mm、76 mm、155 mm炮弹进行的高速弹道试验数据回归得出，适用于侵彻钢筋混凝土侵彻深度的计算。

(2)

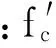
(3)Young公式：最早于1967年提出，经过多次试验修正为1997年的Young公式。主要针对强度低于35 MPa的钢筋混凝土及冻土、黏土等提出。

(3)

式中：S为可侵彻指标，无试验资料可据，可取S=0.9；N为弹头形状影响系数；A为弹体截面面积(m2)；Ke=1；P为混凝土体积配筋率；te为混凝土使用时间(年)，取te=1；Te为被侵彻物厚度与弹体直径之比，一般取0.5≤Te≤6，其它符号意义及单位同前。

(4)SAPL公式：

(4)

式中:ρt为混凝土密度(kg/m3)，KRQD是反映岩石和混凝土质量的定量指标，介于0～100，对于混凝土材料取KRQD=50，其它符号意义及单位同前。

(5)修正“BLZ”公式：2006年由吕晓聪在原有“BLZ”公式基础上把钢纤维特征参数及材料韧度引入后提出。该公式适用于被侵彻物钢纤维含量≤6%时侵彻深度的计算。

(5)

式中：η0为未加钢纤维的混凝土韧度；η为钢纤维混凝土韧度；β为钢纤维含量特征参数的函数，且有β=-0.0194λf+1.6267；λf为钢纤维含量特征系数，λf=ρflf/df，其中ρf、lf、df分别为钢纤维体积掺量率(V%)、长度(mm)，直径(mm)，其它符号意义及单位同前。

1.2 公式计算用参数

(1)钻地弹：巨型钻地弹GBU-57长度6.2 m，弹体直径0.8 m，弹体重约14.0 t，弹体入射角0°，垂直入射。

(2)骨料：显微硬度分别为2.44 GPa、3.12 GPa、5.21 GPa、7.74 GPa和10.85 GPa，粒径均为1 mm～3 mm的石灰石砂，玄武岩砂，石英砂，高铝矾土砂和棕刚玉砂。

(3)混凝土：普通混凝土和高硬度钢纤维混凝土各性能指标如表1所示，其中高硬度钢纤维混凝土是指以棕刚玉为骨料的钢纤维混凝土，去除钢纤维后韧度η0为0.89 MPa。

(4)已知条件：钻地弹GBU-57侵彻普通混凝土防御设施的深度为60 m。

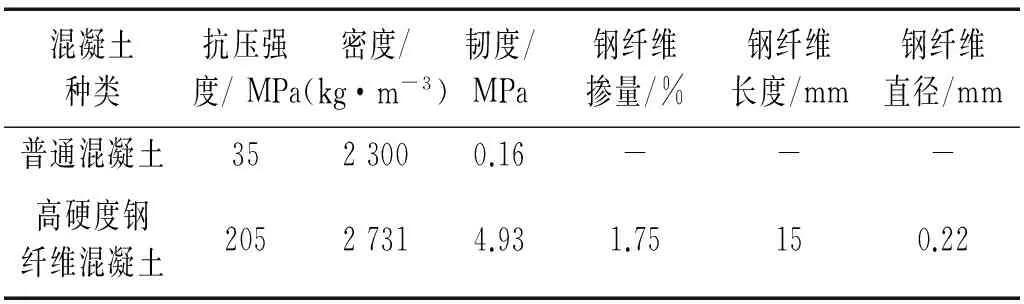
表1 计算用混凝土相关参数

1.3 评估结果与分析

首先对普通混凝土和高硬度钢纤维混凝土进行侵彻试验。侵彻试验多集中于破坏性较大的子弹侵彻研究[6-8]，相关试验仅能在与军工相关的大型实验基地才能实现，测定困难。由于周布奎指出弹体在侵彻过程中，弹、靶材料的破碎以及弹、靶之间的摩擦是消耗弹体动能的主要因素[9]，而钻地弹侵彻过程主要是靠其较高的动能，可见，混凝土材料的耐磨性直接影响着钻地弹的侵彻能力。为了更接近钻地弹侵彻的实际情况，本文采用作者提出的一种利用普通钻床在一定荷载、转速、时间下对混凝土钻磨的快速简便的钻磨试验方法[10]来表征钻地弹的侵彻破坏。

运用钻磨试验方法对普通混凝土和高硬度钢纤维混凝土进行钻磨研究，在试验条件相同时，高硬度钢纤维混凝土120 sec钻磨深度为2.7 mm，而普通混凝土28 sec却达40.0 mm。即钻地弹GBU-57侵彻普通混凝土深度为60 m时，侵彻高硬度钢纤维混凝土仅0.95 m，侵彻深度是普通混凝土的1.6 %。

同时采用BLZ、ACE、Young、SAPL和修正“BLZ”公式进行侵彻深度的计算。图1为五种侵彻公式下钻地弹侵彻普通混凝土和高硬度钢纤维混凝土时侵彻深度与接触速度的拟合对比曲线。表2为根据相应侵彻公式，钻地弹侵彻普通混凝土60 m对应的接触速度侵彻高硬度钢纤维混凝土时的侵彻深度。

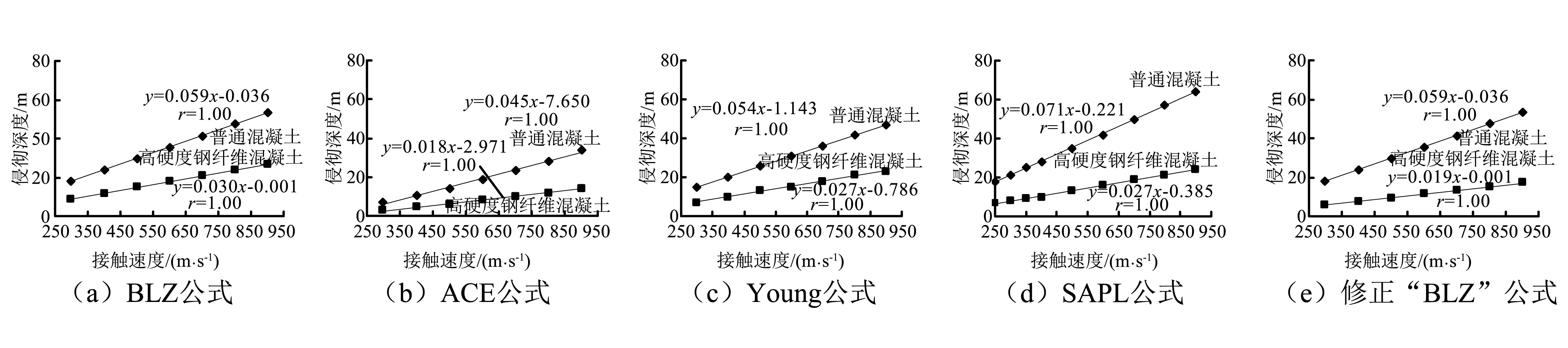
图1 不同侵彻公式时侵彻深度与接触速度的关系Fig.1 Relationships between penetration depth and contact velocity with different formula

由图1可以看出，采用五种侵彻公式时，随着接触速度的增加，普通混凝土和高硬度钢纤维混凝土的侵彻深度均呈较好的直线增长趋势，且普通混凝土侵彻深度的增幅均高于高硬度钢纤维混凝土；由表2可知五种侵彻公式中，采用BLZ、ACE、Young、SAPL公式时，高硬度钢纤维混凝土侵彻深度为普通混凝土的38%～50%，相比修正“BLZ”的19%要大得多。这主要是Young公式适用于强度较低的混凝土靶材，而SAPL、BLZ、ACE只考虑混凝土靶材的抗压强度，而修正的“BLZ”公式由于另外考虑了钢纤维混凝土韧度，则高硬度钢纤维混凝土侵彻深度显著缩小，为普通混凝土的19%，但与前述钻磨方法下实测钻磨深度的1.6%仍有显著差距，这可能是由于该侵彻公式是建立在普通硬度骨料的基础上，而高硬度钢纤维混凝土采用高硬度骨料，因此造成侵彻深度较实测值要大。

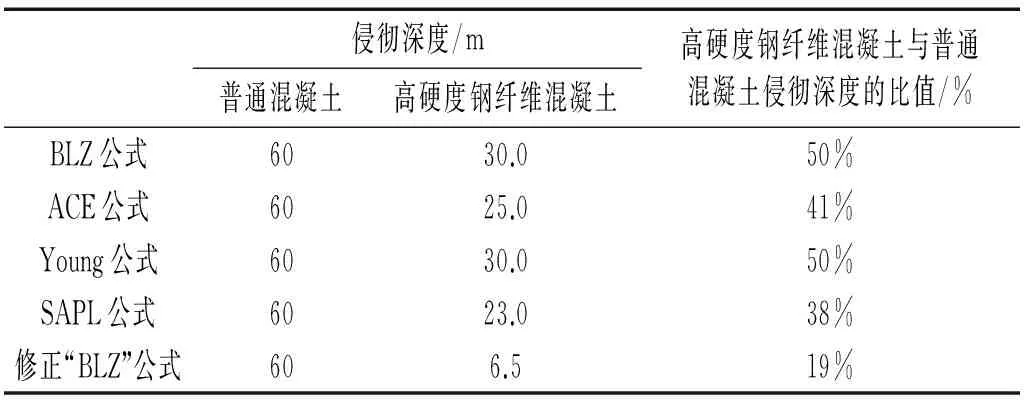
表 2 不同混凝土侵彻深度对比

2 修正ACE公式的建立

综合上述采用各侵彻公式，多以考虑钻地弹性能参数和防御设施抗压强度为主，尽管修正“BLZ”公式把钢纤维混凝土韧度考虑在内，但对于骨料硬度未考虑，造成实测值误差较大。由于ACE公式为美国陆军工程兵用炮弹高速弹道试验数据进行回归得出，具有一定的可靠性；且在20多种计算武器侵彻混凝土材料的经验公式中占有一定的作用，故在此建立修正ACE公式。该公式把钢纤维混凝土韧度η和骨料硬度Na均考虑在内，更准确的用来预测钻地弹的侵彻深度。由于半穿甲战斗部侵彻实验中侵彻深度测定难度较大，为此首先假定半穿甲战斗部侵彻实验得到的侵彻深度和实际钻磨深度具有一定的对应关系。

2.1 修正参数的确定

在上述高硬度钢纤维混凝土基本配合比下，更换不同显微硬度骨料，利用钻磨试验方法进行骨料显微硬度与钢纤维混凝土钻磨深度关系的研究，其结果如图2所示。由图可以看出，随着骨料显微硬度的增加，钢纤维混凝土的钻磨深度呈曲线下降趋势，且钻磨深度与骨料硬度Na1.337成反比关系。

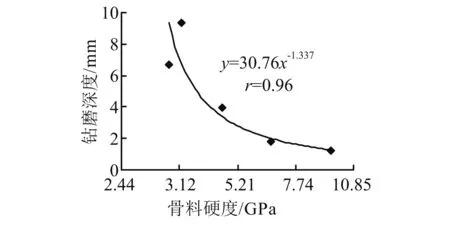
图2 骨料硬度与钻磨深度的关系Fig. 2 Relationships between aggregate hardness and penetration depth

根据王斌等[11]在进行的钻地武器对钢纤维混凝土侵彻的研究中指出，混凝土侵彻深度与混凝土韧度η0.42成反比关系。故修正ACE公式可以用式(6)来表示。

(6)

式中：η为韧度(MPa)；Na为显微硬度(GPa)；K0为修正系数。

2.2 修正ACE公式的建立

已知巨型钻地弹GBU-57侵彻35 MPa普通混凝土时，侵彻深度为60 m。在此认为普通混凝土所采用骨料为显微硬度较低(2.44 GPa)的石灰石砂，已知数据代入式(6)，可求得K0=1.15×10-3。则修正ACE公式为

(7)

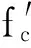
2.3 修正ACE公式的验证

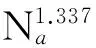
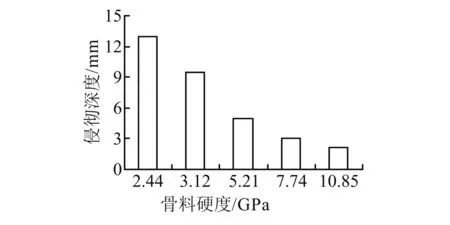
图3 不同硬度骨料时钢纤维混凝土的侵彻深度Fig.3 Contrast between calculated results and test results

下，骨料的硬度越高抵抗钻磨的阻力也越大，钻磨深度越小的缘故。当钻地弹侵彻普通混凝土60 m对应的接触速度侵彻高硬度钢纤维混凝土的深度仅2.1 m，即高硬度钢纤维混凝土侵彻深度为普通混凝土的3.5%，与2.3节实测钻磨深度1.6%的误差较小，从而也证明了该修正ACE公式的合理性。

3 结 论

(1) 运用防护工程研究应用较为广泛的五种侵彻公式对普通混凝土和高硬度钢纤维混凝土抗侵彻性能进行评估，其侵彻深度为普通混凝土的19%～50%，实际耐钻磨试验深度仅为普通混凝土的1.6%，这主要是由于评估方法没有完全考虑骨料硬度和钢纤维混凝土材料韧度的缘故。

(2) 提出修正ACE公式，该修正公式充分考虑了骨料硬度和钢纤维混凝土韧度，且与实测数据符合良好，该公式适用于不同硬度骨料、不同材料韧度的钢纤维混凝土。

[1] 严少华.高强钢纤维混凝土抗侵彻理论与试验研究[D].南京:解放军理工大学, 2001.

[2] 许金余,张志刚,毕征. 防护工程设计原理[D].西安：空军工程大学, 2004.

[3] YOUNG C W. Penetration Equations[R]. SNL: UAS, SAND97-2426/UC-705, 1997, 5-8.

[4] ACE. Fundamental of Protective Design[R]. Report AT1207821, 1946.

[5] 吕晓聪, 许金余. 弹体对钢纤维混凝土侵彻深度的计算研究[J]. 弹箭与制导学报, 2006, 26(1): 89-92. LÜ Xiaocong, XU Jinyu. The study of the calculation about the projectile penetrating the steel-fiber concrete [J]. Journal of Projectiles Rockets Missiles and Guidance, 2006, 26(1): 89-92.

[6] KAMAL I M，ELTEHEWY E. Projectile penetration of reinforced concrete blocks: test and analysis [J]. Theoretical & Applied Fracture Mechanics, 2012，60(1)：31-37.

[7] 刘瑞朝，吴飚，张晓忠，等. 高强高含量钢纤维混凝土抗侵彻性能实验研究[J].爆炸与冲击，2002，22(4): 368-372. LIU Ruichao，WU Biao，ZHANG Xiaozhong，et al. Tests on resisting projectiles penetration of high strength volume steel fiber concrete [J]. Explosion and Shock Waves，2002，22(4): 368-372.

[8] BLUDAU C，KEUSER M，KUSTERMANN A. Perforation resistance of high-strength concrete panels [J]. ACI Struct J，2006，103：188-195.

[9] 周布奎, 唐德高, 周早生，等. 着靶速度对刚玉块石混凝土抗侵彻性能的影响[J].爆炸与冲击，2005，25(1): 59-63. ZHOU Bukui, TANG Degao, ZHOU Zaosheng, et al. Study of influence of hit velocity on the anti-penetration behavior of nubbly corundum concrete [J]. Explosion and Shock Waves，2005，25(1): 59-63.

[10] 孙蓓, 林志翔, 桂志伟. 超高强混凝土耐钻磨性能的研究[J]. 混凝土与水泥制品，2015(6): 24-28. SUN Bei, LIN Zhixiang, GUI Zhiwei. Research of drill-grinding property mechanism of ultra-high strength concrete [J]. China Concrete and Cement，2015(6)：24-28.

[11] 王斌, 金丰年, 徐汉中. 武器侵彻钢纤维混凝土深度的实用计算方法[J]. 爆炸与冲击, 2004, 24(4): 376-381. WANG Bin, JIN Fengnian, XU Hanzhong. The engineering method for calculating the depth of penetrating steel fiber concrete [J]. Explosion and Shock Waves，2004, 24(4): 376-381.

Calculation method for the penetration depth of steel-fiber concrete

SUN Bei1, LIN Zhixiang2, JIAO Chujie1

(1. School of Civil Engineering, Guangzhou University, Guangzhou 510006, Chian;2. State Key Laboratory of Green Building Materials, China Building Materials Academy, Beijing 100024, China)

The penetration resistances of ordinary concrete and steel fiber reinforced concrete mixed with high hardness aggregate were evaluated by virtue of a semi-empirical formula, based on rather wide penetrating experiences. The application area and limitations of the formula were analyzed. A revisional ACE formula was put forward by introducing the hardness of aggregate and the toughness index of steel fiber reinforced concrete. The calculation results by using the revisional formula are in good agreement with the test results, which verifies the rationality of the revisional ACE formula of concrete.

steel-fiber concrete; hardness; toughness index; penetration

国家自然科学基金项目(51278135；51478128)；住房和城乡建设部科研开发项目(2010-K3-27；2010-k4-18)；广州大学重点科技项目培育项目(2015)

2015-10-22 修改稿收到日期： 2016-02-23

孙蓓 女，博士后，1980年4月生

焦楚杰 男，教授，博士生导师，1974年10月生

O383

A

10.13465/j.cnki.jvs.2017.10.032