基于实测数据的某高层建筑结构动力参数和气动阻尼识别

黄铭枫，吴承卉，徐 卿，张凤亮，楼文娟

(1. 浙江大学 建筑工程学院结构工程研究所，杭州 310058; 2. 同济大学 土木工程学院结构与防灾研究所，上海 200092)

基于实测数据的某高层建筑结构动力参数和气动阻尼识别

黄铭枫1，吴承卉1，徐 卿1，张凤亮2，楼文娟1

(1. 浙江大学 建筑工程学院结构工程研究所，杭州 310058; 2. 同济大学 土木工程学院结构与防灾研究所，上海 200092)

根据在北冕台风及汶川远震作用下某270 m高大楼顶层实测得到的加速度响应数据，对该高楼的结构动力参数和气动阻尼进行了识别。采用两种方法识别得到了该大楼的模态振动频率和阻尼比参数。一是经验模态分解(EMD)结合随机减量法(RDT)及希尔伯特黄变换法(简称EMD+RDT)，另外采用了基于贝叶斯理论和快速傅里叶变换的识别方法。利用EMD+RDT法，还得到了阻尼比随加速度幅值的变化规律。两种方法识别得到了非常一致的模态振动频率结果。然而，在台风作用和地震作用下所识别的大楼阻尼比特性却表现出明显不同的特性和规律，这种不同主要是由于在台风作用下的建筑物阻尼包含了气动阻尼成分。如果把地震作用下识别得到的该高楼阻尼比作为结构阻尼比，台风条件下识别得出的阻尼比为总阻尼比，则二者相减可以作为该楼气动阻尼比的估计。

高层建筑；现场实测；加速度响应；自振频率；阻尼比；气动阻尼比

超高层建筑及高耸结构具有柔性高、阻尼低等动力特性，对风荷载比较敏感。原型实测是研究建筑结构在自然极端荷载下动力响应最直接和可靠的手段。我国学者已在高层建筑原型实测领域开展了大量的工作，取得了显著的成果。李国强等[1]对上海金茂大厦开展了实测工作，测试得到了上海金茂大厦的自振频率、阻尼比和振型等动力特性。Li等[2-6]在高层建筑阻尼问题、风场观测和风致响应实测等方面进行了系统的研究工作。建筑物阻尼识别是模态参数识别的重要内容之一。在结构风致加速度响应下识别的阻尼包括结构固有阻尼和气动阻尼。结构固有阻尼主要与建筑结构的材料和结构件连接形式等因素有关[7]。而建筑气动阻尼的产生机理及影响因素主要涉及到结构与风场的相互作用。黄鹏等[8]开展了系列的风洞试验，研究了风速、建筑结构平面是否有修角、截面深宽比以及风向角等对建筑结构气动阻尼的影响。黄鹏等[9]也通过风洞试验研究了周围建筑物的干扰作用对建筑结构气动阻尼的影响。全涌等[10]对某一方形断面高层建筑的气动阻尼进行了研究，得到了该高层建筑横风向及顺风向气动阻尼随折减风速(U/fB)的变化规律。

与高层建筑在台风作用下的风致振动和动力性能现场实测研究工作相比，在地震作用下的高层建筑响应实测及相应动力参数识别工作较为少见。不同于风荷载，地震荷载存在突发性及烈度大等特点，且不存在与建筑结构的气动耦合作用。本文所研究的某270 m高大楼位于香港地区，其顶层安装有加速度传感器，在2008年实测得到了该大楼在北冕台风及汶川远震作用下的加速度响应数据。基于这批数据对大楼的振动模态参数及气动阻尼特性进行了系统的识别和分析。

1 大楼概况及加速度传感器布置

某高楼位于香港，主楼共有73层，总高度达270 m，图1(a)为该楼的平面布置图。该高楼主楼承重系统[11]以井字形巨型剪力墙为主，每隔20层设置巨型桁架转换层，剪力墙沿结构短轴向(Y向)布置。主楼结构的平面为长方形，标准层平面长宽分别为58 m和22 m。该高层建筑结构高宽比大于10，根据现行结构荷载规范的规定[12]，属于对风荷载敏感的结构，且可能有明显的横风向风振效应。该大楼没有采取任何减振措施。图1(b)给出了该楼及周边建筑平面布置图，图中标示出该大楼周边存在的建筑物以及100 m以上高层建筑的高度。

在该高楼顶层安装了加速度传感器，实时监控该高楼的振动状态，测点布置见图1(a)，包括位于角部的测点1和位于结构平面中心的测点2。每个测点位置处均安装有沿着两个正交方向的加速度传感器，其采样频率为20 Hz，用于同步测量建筑顶层X和Y向加速度响应。该检测系统收集到了2008年5月12日汶川大地震及同年8月6日台风北冕两次动力荷载作用下该大楼的顶层加速度响应数据。本文主要根据这两次结构振动响应实测数据进行分析和研究。

(a) 平面图

(b) 周边环境图图1 某高楼平面及环境布置图Fig.1 Plan view and surroundings of the building

2 台风及地震作用

2.1 台风北冕

台风北冕于2008年8月4日在香港东南约580 km的南海东北部发展成一个热带低气压，并向西北偏西移动，翌日早上升为热带风暴，8月6日凌晨增强为强热带风暴并向西北移动。北冕在上午10时最接近香港，在香港之西南偏南约130 km掠过，中心风力大约每小时115 km，其移动路径见图2，当时香港普遍吹偏东强风至烈风。香港气象台在横澜岛上海拔90 m高度处测得最高每小时平均风速为29.1 m/s，最大3 s阵风风速为38.9 m/s。横澜岛附近录得最低气压为98.75 kPa。为此香港天文台于8月6日5:40分发出8号东北烈风或暴风信号，当时北冕位于香港以南约180 km。6日8:40香港天文台改发8号东南烈风或暴风信号。本文采用2008年8月6日上午10时至11时该高楼顶层加速度传感器采集到的实测风振数据用于模态参数及气动阻尼的识别和分析。

2.2 汶川大地震

汶川大地震发生于北京时间2008年5月12日，震中位于中国四川省阿坝藏族羌族自治州汶川县映秀镇附近(北纬31.02°东经103.37°)，距香港1 440 km，处于香港310°方位角，地震波入射大致方位角参见图1(a)中所示。根据中国地震局数据，此次地震的面波震级达8.0 MS、矩震级达8.3 MW(根据美国地质调查局的数据，矩阵级为7.9 MW),破坏地区超过10万平方千米。地震波及大半个中国及亚洲多个国家和地区，北至辽宁，东至上海，南至香港、澳门、泰国、越南，西至巴基斯坦。根据香港天文台记录，香港地震烈度为Ⅲ级，30名以上市民有震感。本文采用2008年5月12日14时至15时该高楼顶层加速度传感器采集到的实测数据用于结构振动模态参数和结构阻尼比的识别分析。

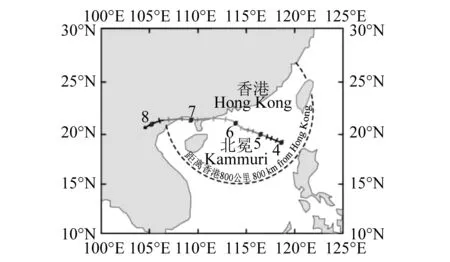
图2 2008年台风北冕(Kammuri)路径图Fig.2 Track of Kammuri in 2008

3 大楼响应数据及分析

图3给出了2008年8月6日上午10时至11时在北冕台风作用下该高楼顶层角部测点1处的X向加速度响应时程。图4(a)则为2008年5月12日14时至15时在汶川大地震主震发生前后该高楼顶层角部测点1处的X向加速度响应时程。

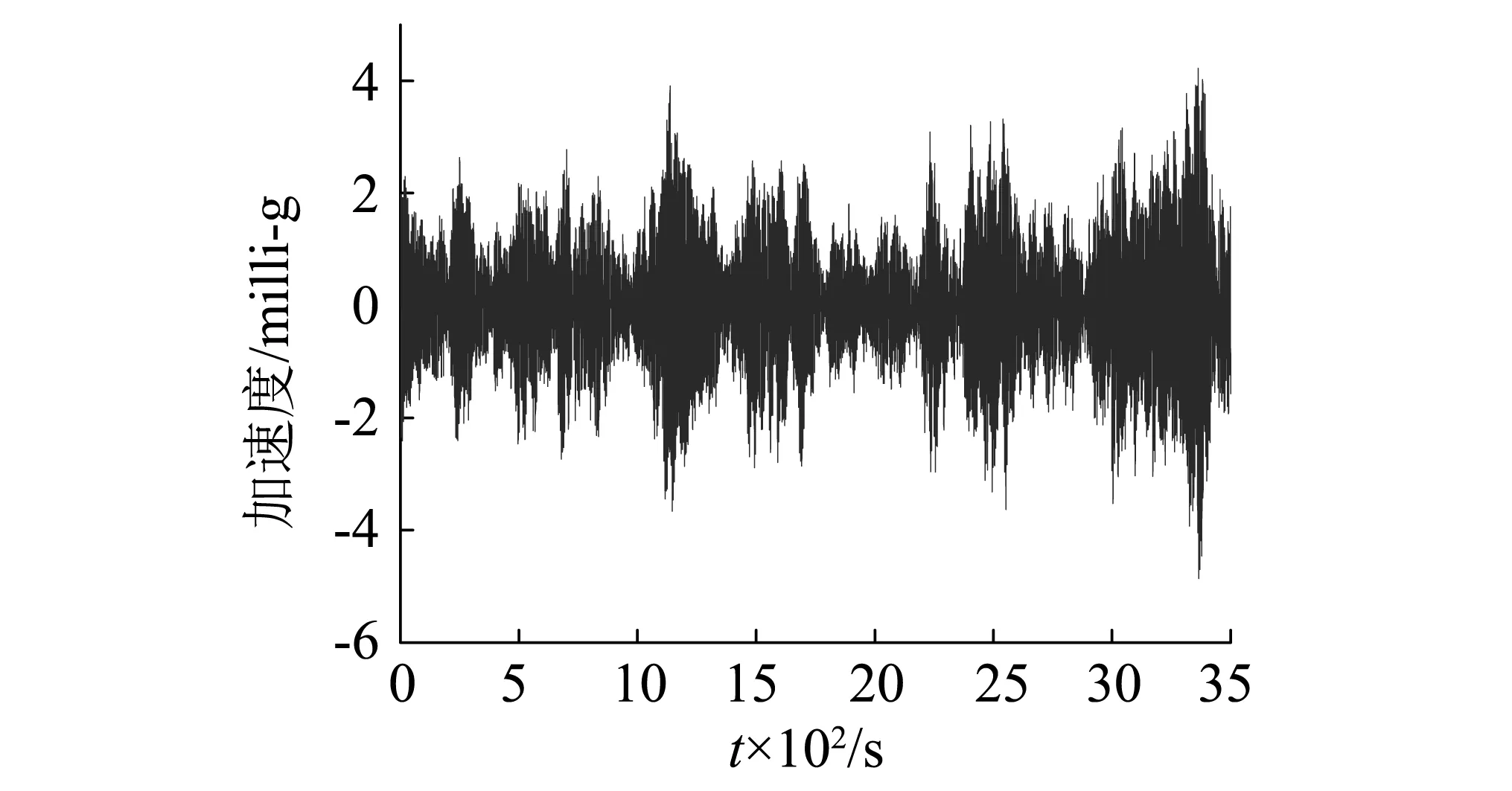
图3 角部测点1北冕台风下X向加速度响应时程Fig.3 Acceleration time history at the corner measuring point under typhoon

由于加速度传感器的数据采集阈值为±10 milli-g，在汶川8.0级大地震作用下，该高楼顶层加速度响应超出了10 milli-g，采集到的峰值数据存在一定的缺口，见图4(b)。从图4(b)中可以看出在2 120～2 160 s时段内存在几个波峰被明显截断，本文采用数值方法对原始数据进行了插值补充，修复完善后的数据在图4(b)中用虚线标示。

虽然汶川大地震震中位置距香港1 440 km，但在其作用下该大楼的加速度响应甚为显著。拟合修复后的数据表明远震作用下该大楼顶层的加速度响应最大值可达到16.53 milli-g。而在北冕台风作用下该楼顶层的加速度响应峰值为5.949 milli-g，远远小于汶川地震作用下的响应峰值。

(a)

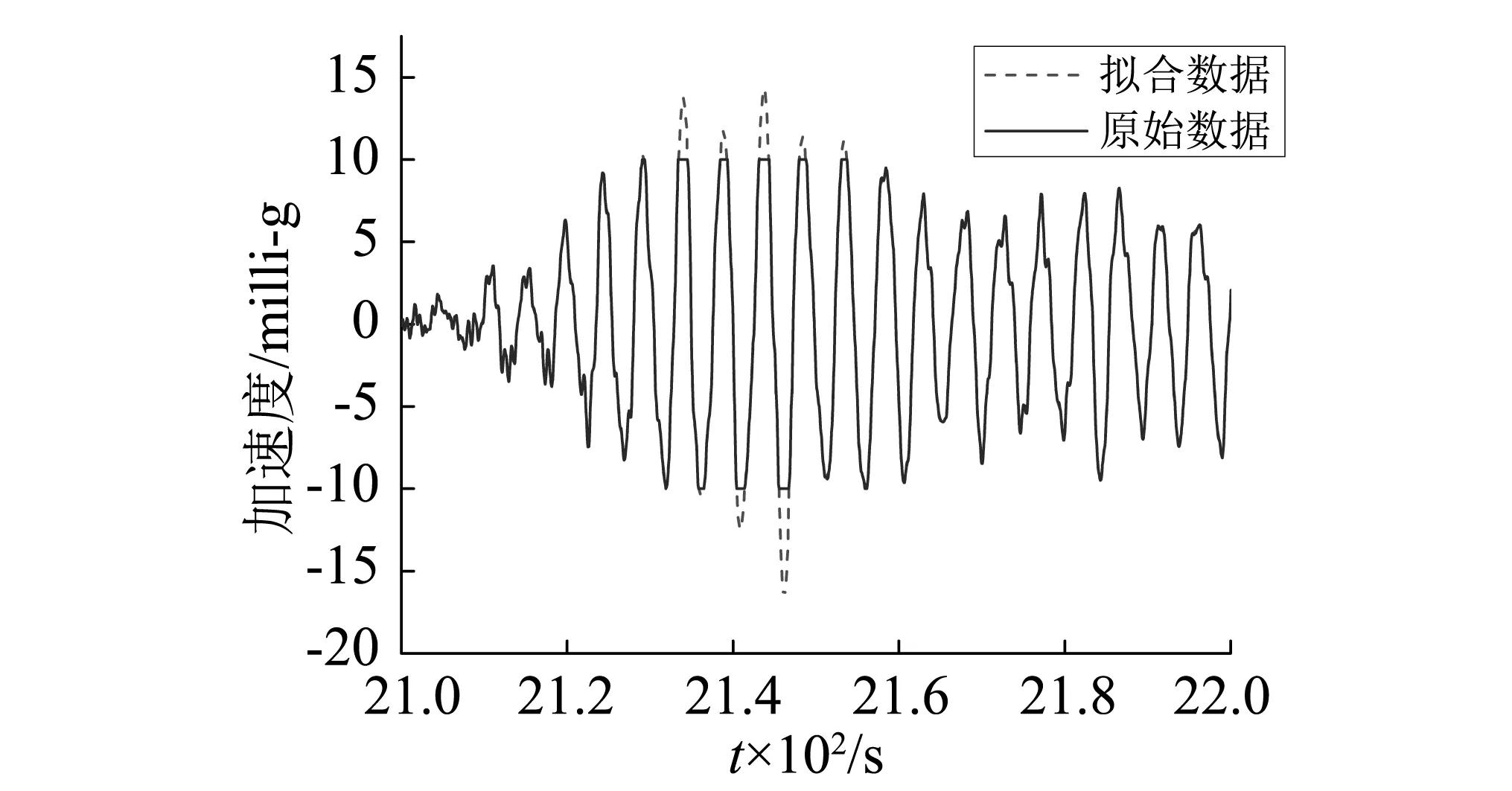
(b)图4 角部测点1远震下X向加速度响应时程Fig.4 Acceleration time history at the corner measuring pointunder earthquake

4 模态参数识别

4.1 识别方法

目前识别自振频率最简单的方法是谱峰值法[13-14](Peak-Picking Method，简称PP法),即拾取响应信号的功率谱密度曲线峰值对应频率作为自振频率。EMD结合随机减量法[15]及希尔伯特黄变换[16-18]是在时域内对信号进行处理识别，得到结构的自振频率及阻尼比。Yuen等[19-21]提出的基于贝叶斯理论的快速FFT(Fast Bayesian FFT)方法是在频域内基于某一共振频率带的单个模态而提出的，快速而高效的运用贝叶斯理论识别结构模态参数。本文主要采用上述三种方法对该高楼进行模态参数的识别，主要包括自振频率，阻尼比及气动阻尼比。

随机减量法是从结构随机响应信号获取结构自由衰减信号的一种非常方便有效的方法。其基本思想是建立在线性系统的叠加原理基础上的：即对于结构随机响应，指定某种条件，将响应中确定性的和随机的两部分实现分离，然后利用统计平均的方法将随机的部分排除掉，过滤出确定性的自由衰减信号。

Hilbert-Huang变换(HHT)包括两部分：经验模态分解(Empirical Mode Decomposition, EMD)得到不同的固有模态函数(Intrinsic ModeFunction, IMF)和利用Hilbert变换得到信号的时频特征。它对信号没有过多要求，能够很好的适用于非线性和非平稳信号。对于一个IMF时间序列X(t), 可以得到它的Hilbert变换结果Y(t)为

(1)

则与X(t)相对应的解析信号为

Z(t)=X(t)+iY(t)=a(t)eiθ(t)

(2)

对上式中幅值a(t)=A0e-ξω0t取对数并进行最小二乘拟合，可以得到斜率-ξω0；对相位角θ(t)=ωdt+φ0进行最小二乘拟合，可以得到斜率ωd。其中：ξ为阻尼比；ωd为结构的有阻尼自振圆频率；ω0为结构的无阻尼自振圆频率。

(3)

(4)

本文采用EMD结合随机减量法得到结构的自由衰减信号，再采用Hilbert变换得到结构的各阶模态参数(上述方法简称EMD+RDT法)。在运用随机减量法过程中，在保证子样本数满足条件的情况下，采用不同的幅值A去截取信号，可以得到不同初始幅值A下的自由振动衰减信号。对不同初始截取幅值下的自由振动衰减信号进行Hilbert变换，并根据式(3)、(4)计算得到自振频率及阻尼比。根据不同截取幅值下的自由衰减信号识别得到的自振频率为一固定值，而得到的阻尼比却会随初始截取幅值的变化而变化，所以认为截取信号幅值是影响阻尼比结果的因素之一。根据上述过程可以得到阻尼比随加速度幅值的变化规律。

另外采用基于贝叶斯理论的快速FFT(Fast Bayesian FFT)方法与上述方法识别结果进行对比。下面给出快速贝叶斯FFT识别方法的基本理论。

对于某个实测的加速度响应信号样本可以表达为

(5)

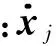
(6)

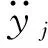
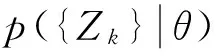
(7)

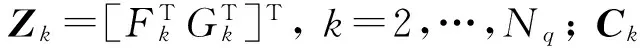
将后验概率密度函数PDF进一步由对数似然函数L(θ)表示。当采集到的信号足够大是，后验概PDF可以用高斯分布的PDF近似，而高斯PDF等价于L(θ)关于θ的二阶泰勒展开式，因此式(7)化简后可表示为

(8)

(9)

(10)

(11)

(12)

(13)

结构的自振频率及阻尼比参数可以通过对式(9)开展无约束优化直接求得。模态参数的后验不确定性可由后验协方差矩阵计算，并且模态频率和模态阻尼比的后验不确定性大小可以根据各自的后验变异系数(c.o.v)进行衡量。值得注意的是，由于Fast Bayesian FFT法中采用了振动信号高信噪比假定和傅里叶变换渐近服从高斯联合分布的假定，该方法对激励信号特性的基本要求是信噪较高且近似满足宽频激励。

4.2 自振频率识别结果

采用谱峰值法对该高楼在两次激励下的顶层加速度响应信号进行自振频率识别。图5和图6分别为该楼在台风和远震作用下顶层加速度响应的功率谱密度图。从两次实测数据得到的加速度响应谱峰值明显，所识别的结构自振频率值直接标注在图中功率谱峰值上。对比图5(a)、(c)可以看出角部测点、中心测点X方向的加速度功率谱图都在0.205 1 Hz处存在波峰，并且对应的谱值最大，可见0.205 1 Hz为结构X向振动的首阶频率；同理对比图5(b)、(d)得出0.346 7 Hz为结构Y向一阶频率。纵观图5中4个功率谱图都存在0.439 5 Hz的波峰，在角部测点对应谱值较大，而在中心测点对应谱值很小，这是由于结构扭转在角部产生较大平动分量，而中心测点的加速度传感器也能感应到由于扭转产生的微小平动分量，从而可以判定0.439 5 Hz为结构的扭转振型频率。另外根据汶川地震作用下对应的大楼顶层加速度响应功率谱(参见图6)作上述分析同样可得到该大楼的结构自振频率，结果列于表1。对比图5和图6的功率谱图可以看出，在台风作用下该高楼的扭转加速度响应分量在4个功率谱图中均存在明显的波峰，而在远震作用下的扭转频率对应的谱峰只在角部测点X向加速度功率谱图中比较明显，说明该高楼在台风作用下引起的扭转响应较大，而远震作用下引起的扭转响应较小。

图5 台风北冕作用下大楼顶层加速度响应功率谱密度Fig.5 Power spectrum density functions of acceleration responses under typhoon

图6 汶川远震作用下大楼顶层加速度响应功率谱密度Fig.6 Power spectrum density functions of acceleration responses under earthquake

在进行EMD分解前为避免模式混淆(Mode Mixing,MM),首先对信号进行滤波处理，消除各阶模态间的影响。结合表1自振频率识别结果，采用带通滤波器，滤波器的上下限值参见表2。对台风及远震作用下的加速度响应时程数据，均采用表2所列参数进行了滤波处理。由于基于贝叶斯理论的快速FFT方法是在频域内基于某一共振频率带的单个模态而提出的，也需要提取各个模态下的频段分量，故也采用根据表2参数滤波后的数据进行模态识别。其中扭转模态信息只从角点处的加速度响应时程数据中提取。随机减量法及希尔伯特-黄变换法(EMD+RDT法)与基于贝叶斯理论的快速FFT法识别得到的结构自振频率见表3。

表1 PP法自振频率识别结果

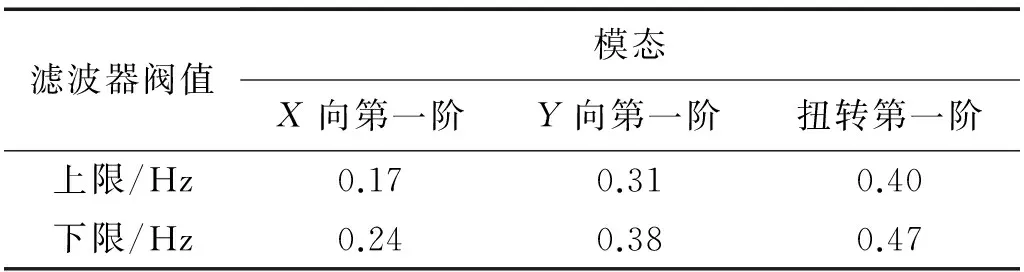
表2 带通滤波器阀值

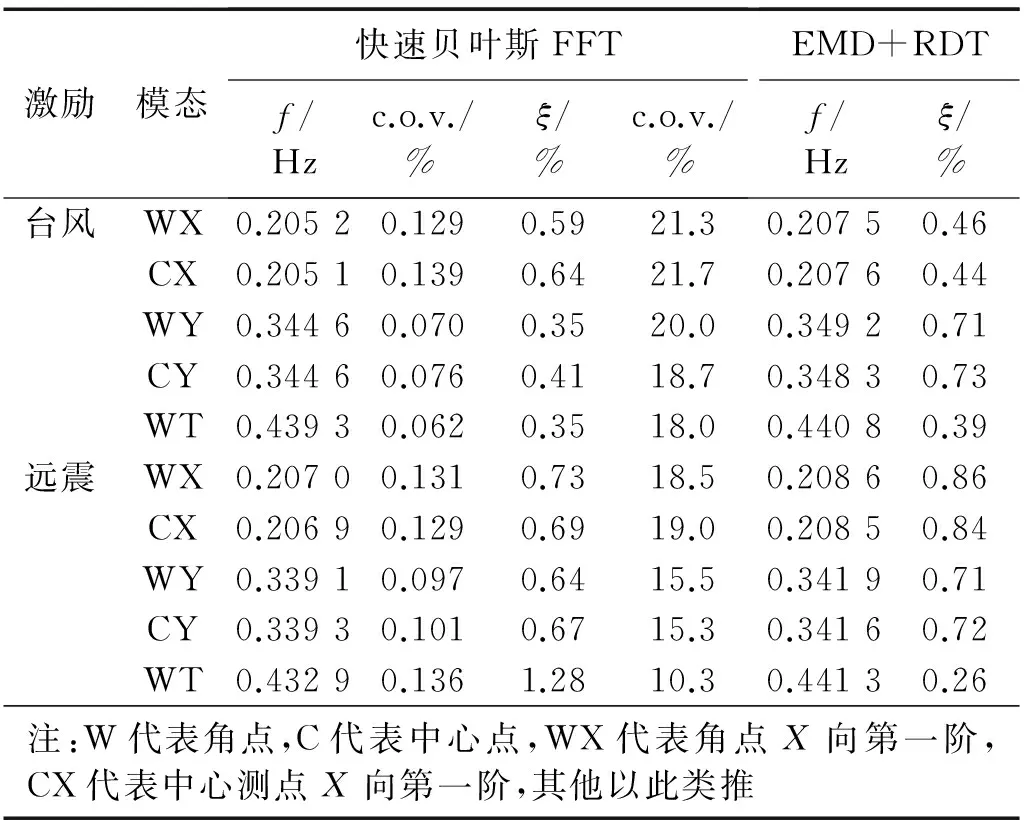
表3 快速贝叶斯FFT法及EMD+RDT法模态参数识别结果

4.3 阻尼比识别结果

对滤波后各阶模态时程选用一系列振幅阀值，利用EMD+RDT法识别得到高楼结构前三阶阻尼比随振动幅值的变化规律。图7和图8分别给出了在台风和远震作用下该大楼的阻尼比识别结果。快速贝叶斯FFT方法识别得到的阻尼比结果与振幅无关，在图7和图8中用虚线标示出其识别得到的最大及最小阻尼比，并用实线标识其偏差范围。从图中可见，两种方法得到的阻尼比估计值有一定的可比性。与Y向和扭转向相比，大楼结构沿X向的加速度响应信号最强，相应的X向振动模态阻尼比沿振动幅值的变化规律也最为明显。如考虑大于1 milli-g的振幅，在台风作用下，X向振动模态阻尼比随着振幅的增加开始逐渐变大，到振幅达到3 milli-g时，阻尼比又趋于稳定，其值在0.6%左右；而在远震作用下，X向振动模态阻尼比也随着振幅的增加而变大，到振幅达到3 milli-g时，阻尼比就基本稳定在1%左右。

根据两种方法对台风及远震作用下加速度响应信号数据的模态阻尼比识别结果也在表3中给出。由于EMD+RDT法的阻尼比结果与截取的信号振幅有关，表3中给出的是所有振幅下阻尼识别结果的平均值。从表3可见，采用快速贝叶斯FFT方法识别得到的阻尼比变异系数明显大于频率的变异系数，这可能与结构阻尼产生机理的复杂性有关。不同外界激励下结构耗能形式会有所差异，导致结构阻尼比与外界激励条件也存在一定的关联。在强台风作用下，由于可能存在的气弹效应，阻尼比与风振振幅之间有着显著的非线性关系(如图7所示)，导致采用快速贝叶斯FFT方法得到的最大阻尼比的变异系数较大。总体来说，除了远震作用下WT模态信号的识别结果，EMD+RDT法识别得到的大楼整体各个振动模态幅值平均阻尼比结果与快速贝叶斯FFT法识别的结果比较符合。而在远震作用下WT模态信号相对是最弱的，可能导致较大的计算识别系统误差。

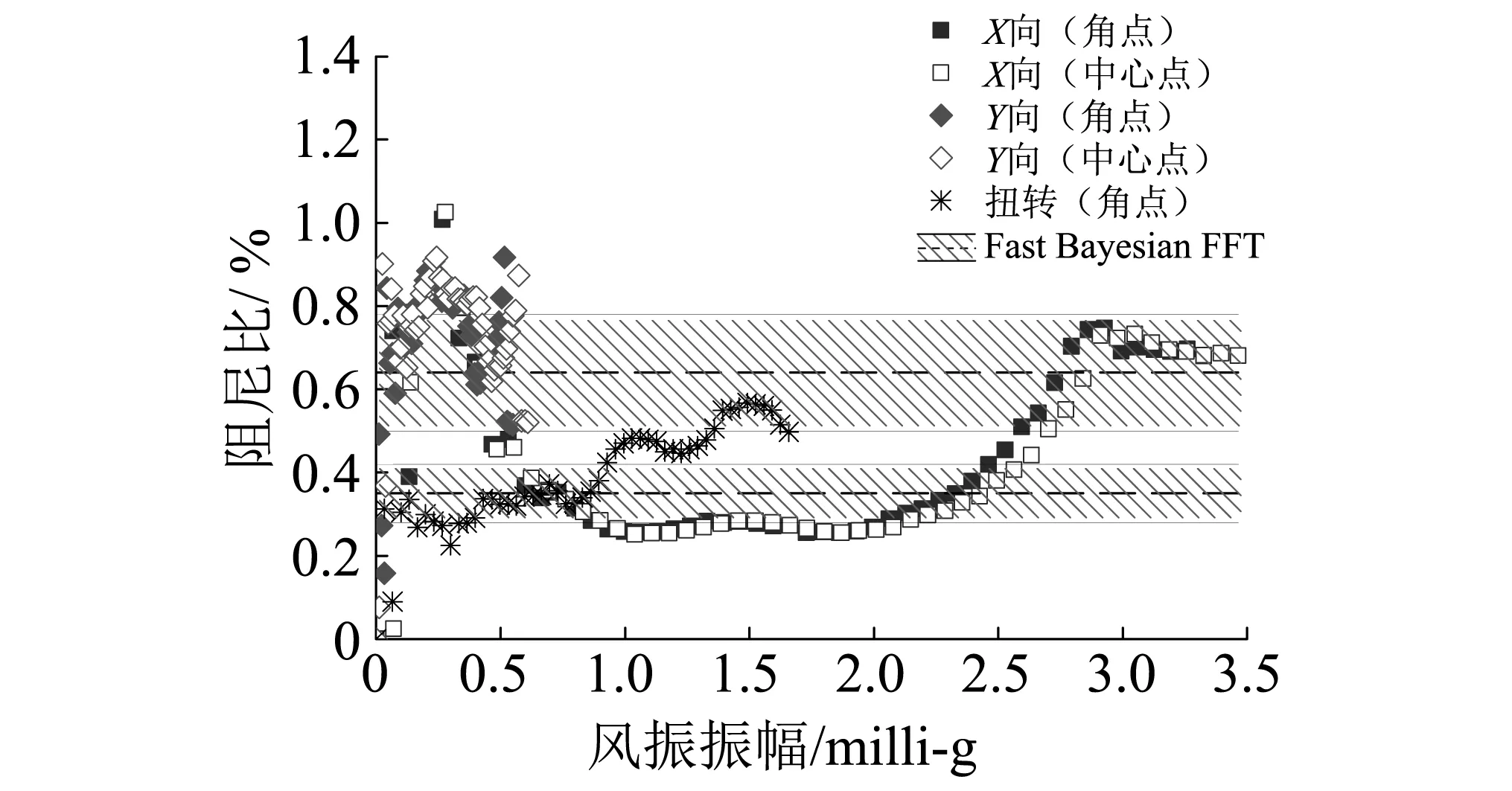
图7 台风作用下大楼前三阶模态阻尼比识别结果Fig.7 Damping ratio with vibration amplitude under typhoon

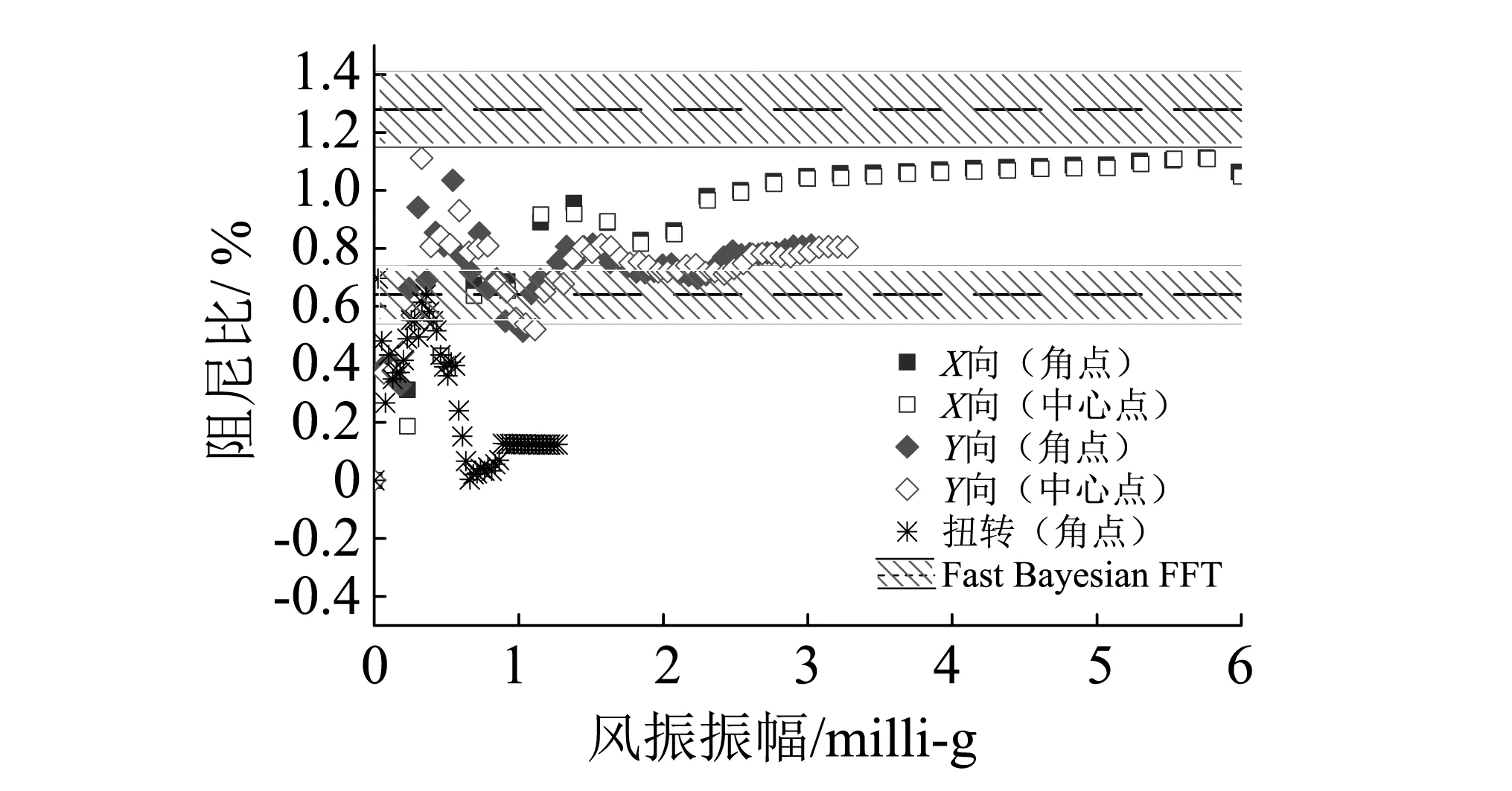
图8 地震下大楼前三阶模态阻尼比识别结果Fig.8 Damping ratio with vibration amplitudeunder earthquake

4.4 气动阻尼比识别结果

气动阻尼是对风与结构相互作用的一种简化描述，主要发生机制在于结构运动对周边风场产生了扰动并形成区别于静态结构的风激励作用。显然气动阻尼是在结构与来流风场耦合作用下产生的，相关研究已经表明，高层建筑横风向气动阻尼在较小折算风速区域和临界风速附近均有可能出现负阻尼。负的气动阻尼将会放大结构的风振响应，若是在结构风振响应计算中忽略气动阻尼项将导致设计偏于危险。基于远震加速度响应数据识别得到的阻尼比可以近似作为该大楼的结构阻尼比。而基于台风作用下加速度时程数据识别得到的阻尼比应该是结构阻尼比和气动阻尼比之和，这样风振阻尼比和地震阻尼比的差值可以作为该大楼在台风作用下气动阻尼比的近似估计。图9给出了各阶模态下识别出的气动阻尼比结果。从图中可以看出：Fast Bayesian FFT方法识别得到的气动阻尼比为负值；同时由EMD+RDT法得到的气动阻尼比随加速度幅值变化曲线可以看出，在该次台风下气动阻尼比在加速度幅值较小时(1 mill-g)就出现负值，当加速度幅值大于3 mill-g时，X向平动模态的气动阻尼比基本稳定在-0.5%左右。黄鹏、顾明研究认为当一个高层建筑受到周围其他建筑物的气动干扰时，气动阻尼比也会出现负值。从图1(b)可见，该大楼处于大型城市中心地带，大楼周边建筑物密集分布，且存在不少高层建筑。因此，对于该大楼X向平动模态的负气动阻尼比也可以认为是在现场实测状况下受到了周围建筑的明显气动干扰作用。而扭转模态的气动阻尼比则为正的。由于Y向平动模态的振幅太小，导致识别的气动阻尼比结果不是很稳定。

由于阻尼值本身比较小，实测信号受到的干扰因素比较多，因此通过实测数据来识别高层建筑阻尼特性容易产生比较大的误差。本文采用Fast Bayesian FFT法能得到所识别建筑物模态阻尼比参数的变异性，因此对于后续计算得到的气动阻尼也能给出一定的误差估计。图9中虚线指示了Fast Bayesian FFT法对气动阻尼比的最优估计值，而阴影区域为其误差估计范围。对于EMD+RDT法得到的气动阻尼尚不能给出其误差的估计。但与Fast Bayesian FFT法相比，EMD+RDT方法的识别结果显然也存在较大的误差，其原因一方面与实测信号的强度有关。如图7和图8所示，对于信号强度较弱的台风作用下Y向和远震作用下扭转向阻尼识别结果，EMD+RDT方法与Fast Bayesian FFT存在明显的偏差。另一方面，EMD+RDT方法的识别过程中需要设定不同阈值来得到不同振幅下的阻尼比，但不同阈值下随机减量的效果并不完全相同，从而带来与设定阈值有关的误差。

图9 前三阶气动阻尼比随振幅变化规律Fig.9 Aerodynamic damping ratio of the first three modes

5 结 论

通过对某高楼在台风北冕和汶川远震作用下顶层加速度响应数据的分析和识别，得到了该高层建筑的结构动力及气动阻尼参数等，主要结论如下：

(1)对应北冕台风和汶川地震作用下的两次现场实测振动数据，分别采用峰值法识别出了相应的结构平动及扭转模态振动频率，其结果相差不超过2.3%。并且与EMD+RDT法及Fast Bayesian FFT法识别得出的结构频率较接近，说明该大楼的振动频率识别结果是真实可靠的。

(2)在北冕台风和汶川地震作用下识别得到的阻尼比结果随加速度幅值的变化存在一定的规律：考虑大于1 milli-g的振幅，在台风作用下，X向振动模态阻尼比随着振幅的增加开始逐渐变大，到振幅达到3 milli-g时，阻尼比又稳定在0.6%左右；而在远震作用下，X向振动模态阻尼比也随着振幅的增加而变大，到振幅达到3 milli-g时，阻尼比基本稳定在1%左右。总体来说，除了远震作用下WT模态(扭转)信号的识别结果，EMD+RDT法识别得到的大楼整体各个振动模态幅值平均阻尼比结果与快速贝叶斯FFT法识别的结果比较符合。

(3)由于台风作用下所识别的阻尼也包含了气动阻尼成分，而地震作用下所识别的阻尼比可以近似认为是该大楼的结构阻尼，这样该大楼在台风作用下的气动阻尼比可以从风振阻尼比减去地震作用下的阻尼比而得到。结果显示该大楼在X向平动风振振幅超过1 mill-g时表现出明显的负气动阻尼比，其值在-0.5%左右。该楼顶的风速实测表明当时的平均风速为13 m/s，这个条件下该楼的折减风速约在2与3之间，这个负气动阻尼显然是在低风速台风下出现的。这个负气动阻尼的出现，可能与该楼受到了周围建筑的气动干扰效应有关。该大楼低风速台风下负气动阻尼的验证及其具体产生机理值得后续进一步研究。但建筑物在风振过程中识别得出的总阻尼仍然是正的。所以实测的风振信号(如图3所示)主要表现出随机风振的波形，没有发散振动等现象发生。

[1] 李国强，陈素文，李杰,等. 上海金茂大厦结构动力特性测试[J]. 土木工程学报，2000,33(2):35-39. LI Guoqiang, CHEN Suwen, LI Jie, et al. Measurements of dynamic properties of Shanghai Jinmao mansion[J].China Civil Engineering Journal, 2000,33(2):35-39.

[2] LI Q S, FANG J Q, JEARY A P, et al. Full scalemeasurement of wind effects on tall buildings[J].Journal of Wind Engineering and IndustrialAerodynamics,1998,74/75/76:741-750.

[3] LI Q S, WU J R, LIANG S G, et al.Full-scale measurements and numerical evaluation of wind-induced vibration of a 63-story reinforced concrete super tall building[J].Engineering Structures,2004,26(12):1779-1794.

[4] LI Q S, XIAO Y Q, WONG C K. Full-scale monitoring of typhoon effects on super tall buildings[J]. Journal of Fluids and Structures, 2005, 20(5):697-717.

[5] LI Q S, FU J Y, XIAO Y Q, et al. Wind tunnel and full-scale study of wind effects on China’s tallest building[J]. Engineering Structures, 2006, 28(12):1745-1758.

[6] 李秋胜，郅伦海，段永定,等.台北101大楼风致响应实测及分析[J].建筑结构学报，2010，31(3):24-31. LI Qiusheng, ZHI Lunhai, DUAN Yongding, et al. Full-scale measurements and analysis of wind-induced response of Taipei 101 Tower[J].Journal of Building Structures, 2010，31(3):24-31.

[7] 邹良浩，梁枢果，顾明. 高层建筑气动阻尼评估的随机减量技术[J]. 华中科技大学学报(城市科学版)，2003,20(1):30-33. ZOU Lianghao, LIANG Shuguo, GU Ming. Evaluation of aerodynamic damping in wind-induced vibration of tall buildings by random decrement technology[J]. Journal of Huazhong University of Science and Technology (Urban Science Edition), 2003,20(1):30-33

[8] 黄鹏，顾明，全涌. 高层建筑气动阻尼的试验研究[C]∥第十二届全国结构风工程学术会议论文集.西安，2005.

[9] 黄鹏，顾明.受扰情况下高层建筑气动阻尼的试验研究[C]∥第六届全国风工程及工业空气动力学学术会议.北京，2003.

[10] 全涌，顾明.方形断面高层建筑的气动阻尼研究[J].工程力学，2004,21(1):26-30.

QUAN Yong, GU Ming. Wind tunnel test study of aerodynamic damping of super highrise buildings [J]. Engineering Mechanics, 2004,21(1):26-30.

[11] 林巍，黄铭枫，郭中秀,等.台风下香港K11大楼风振响应实测及分析[J].深圳大学学报理工版,2012,29(1):45-50. LIN Wei, HUANG Mingfeng, GUO Zhongxiu, et al. Full-scale measurement and analysis of K11 building in Hong Kong during typhoon[J]. Journal of Shenzhen University Science and Engineering, 2012,29(1): 45-50.

[12] 中华人民共和国国家标准.建筑结构荷载规范: GB 50009—2010[S].北京：中国建筑工业出版社，2010.

[13] 姜浩，郭学东，杨焕龙.预应力混凝土桥梁模态参数识别方法[J].沈阳建筑大学学报，2009，25(5):914-919. JIANG Hao, GUO Xuedong, YANG Huanlong. Research on modal identification method of pre-stressed concrete bridge[J].Journal of Shengyang Jianzhu University, 2009，25(5):914-919.

[14] 张毅刚，刘才伟，吴金志,等，适用空间网格结构模态识别的改进功率谱峰值法[J].振动与冲击，2013,32(9):10-15. ZHANG Yigang, LIU Caiwei, WU Jinzhi, et al.Improved power spectrum peak method applied in themodal identification of spatial lattice structures[J].Journal of Vibration and Shock, 2013,32(9):10-15.

[15] 张西宁，屈梁生.一种改进的随机减量信号提取方法[J].西安交通大学学报，2000,34(1):106-107. ZHANG Xining, QU Liangsheng. Improved method for extracting of random decrement signal[J]. Journal of Xi’an Jiaotong University , 2000,34(1):106-107.

[16] 顾远生，李春祥，刘畅.基于希尔伯特-黄变换的超高层建筑模态参数识别[J].建筑科学，2009,25(3):44-48. GU Yuansheng, LI Chunxiang, LIU Chang. Identification of modal parameters of super high buildings based on Hilbert-Huang Transform[J]. Building Science, 2009,25(3):44-48.

[17] 彭程，张立民，李原辉，等.利用改进的EMD和随机减量法识别模态参数[J].噪声与振动控制，2011,12(6):53-56. PENG Cheng, ZHANG Limin, LI Yuanhui, et al. Identification of modal parameters using improved EMD and random decrement method[J]. Noise and Vibration Control, 2011,12(6):53-56.

[18] CHEN Bo, YANG Qingshan, WANG Ke, et al.Full-scale measurements of wind effects and modal parameter identification of Yingxian wooden tower[J].Wind and Structures,2013,17(6):609-627.

[19] YUEN K V, KATAFYGIOTIS L S.Bayesian fast Fourier transform approach for modal updating using ambientdata[J].Advances in Structural Engineering, 2003,6(2)：81-95.

[20] AU S K. Fast Bayesian FFT method for ambient modal identification with separatedmodes[J].ASCE Journal of Engineering Mechanics，2011，137(3)：214-226.

[21] AU S K，ZHANG F L. Ambient modal identification of a primary-secondarystructure by Fast Bayesian FFT method[J].Mechanical Systems and Signal Processing，2012，28：280-296.

Structural dynamic and aerodynamic parameters identification for a tall building with full-scale measurements

HUANG Mingfeng1, WU Chenghui1, XU Qing1, ZHANG Fengliang2, LOU Wenjuan1

(1.College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058,China;2.College of Civil Engineering, Tongji University, Shanghai 200092,China)

Based on the two sets of acceleration response data, full-scale measured on a 270 m tall building in Hong Kong during Typhone Kammuri and 512 Wenchuan earthquake in 2008, the dynamic modal properties of the tall building were identified by two methods. One is the traditional method of empirical mode decomposition (EMD) combined with the random decrement technique (RDT), the other is the recently proposed fast Bayesian method using the fast Fourier transform (FFT). The natural frequency of each mode identified by these two different methods is very close to each other, while noticeable difference is observed between the damping ratio results corresponding to each mode. The identified results under the two excitation events were also compared. As expected, the wind-induced acceleration data suggest almost the same natural frequency values as those identified from the acceleration data under the long-distance earthquake. However, the damping ratios of the tall building corresponding to Wenchuan earthquake are found to be larger than those under typhoon excitation. The subtraction results between these two sets of damping ratios might be considered as the estimation values of aerodynamic damping ratios.

tall building; full-scale measurement; acceleration;natural frequency; damping ratio; aerodynamic damping ratio

国家自然科学基金资助(51578504)；浙江省公益性技术应用研究计划资助项目(2012C21059)

2015-04-08 修改稿收到日期： 2016-04-20

黄铭枫 男，博士，教授，博士生导师，1976年生

TU311

A

10.13465/j.cnki.jvs.2017.10.006