不同纤维长度的混杂钢纤维混凝土本构模型

霍琳颖，毕继红，2，*，赵 云，王照耀

（1.天津大学建筑工程学院，天津 300350；2.天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072）

钢纤维混凝土（SFRC）在工程中的应用越来越普遍，钢纤维的加入能有效改善混凝土抗拉强度低、韧性差、易开裂等缺陷［1-2］.Park 等［3］发现，在单向受拉状态下，SFRC 中的短钢纤维主要在微裂纹时期发挥桥接作用，长钢纤维更多在宏观裂纹阶段起到增强作用.Zhou 等［4］通过比较不同钢纤维配比下混杂钢纤维混凝土（HySFRC）的强度，发现长钢纤维对残余强度的贡献明显大于短钢纤维.Chang等［5］通过四点弯曲试验，探究了混杂钢纤维对HySFRC 开裂后力学性能的影响.Turk 等［6］研究了混杂钢纤维对HySFRC 力学性能的影响，发现长钢纤维体积分数为80%时HySFRC 具有最优的抗弯性能.

许多学者基于热动力学理论和SFRC 的试验研究，为SFRC 建立了一系列本构模型.李杰等［7］考虑损伤和塑性的耦合效应，建立了损伤本构模型.池寅等［8］基于塑性损伤模型，建立了钢纤维混凝土的塑性损伤本构模型.但目前为止，尚无针对HySFRC 建立的本构模型.本文基于经典的混凝土弥散开裂本构模型，将混杂钢纤维应力作为附加应力，从而建立了混杂钢纤维混凝土的本构模型.通过对混杂钢纤维混凝土试验数据的数值模拟，验证了所建立本构模型的正确性.

1 基体中的混杂钢纤维

短钢纤维的自身体积较小，在相同钢纤维体积分数的钢纤维混凝土中，短钢纤维在混凝土基体中的根数要明显多于长钢纤维.短钢纤维由于根数多的优势，对混凝土开裂前期的微观裂缝起到明显增强作用.长钢纤维基于长度优势可持续为开裂后的混凝土提供增强作用，对混凝土残余强度有明显提高作用［9］.混杂钢纤维的体积分数Vf由2 种长度的钢纤维各自的体积分数构成，即：

式中：Vf-s、Vf-l分别为短、长钢纤维的体积分数.

混杂钢纤维混凝土中，长钢纤维长度和直径分别为Lf-l、df-l；短钢纤维长度和直径分别为Lf-s、df-s.为了便于理论推导计算混杂钢纤维的增强作用和建立本构模型，假设基体中长钢纤维长度为短钢纤维长度的2 倍.另外，假设在混杂钢纤维混凝土浇筑过程中，通过充分地搅拌振捣，钢纤维在混凝土基体中取向三维随机、分布完全均匀［10］.且混凝土基体中掺入不同长度钢纤维不影响钢纤维取向的三维随机性［10-11］.混杂钢纤维在混凝土基体中的取向系数如式（2）所示.

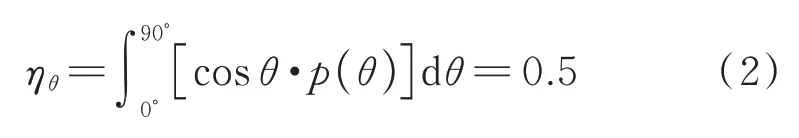
式中：ηθ为混杂钢纤维在混凝土基体中的取向系数；θ为钢纤维与开裂面法线方向的夹角；p(θ)为钢纤维在基体中的概率分布密度函数.

利用混杂钢纤维取向系数，计算出长、短钢纤维在开裂面法线方向的投影值，即长、短钢纤维的有效长度lf-l、lf-s：

2 混杂钢纤维的有效根数及埋深长度

混凝土开裂后，开裂面上的钢纤维两侧同时受力，埋深较短一侧因抗拉拔力更小而首先被拔出.较短一侧的埋深被定义为钢纤维有效埋深长度.图1 给出了混凝土单元中短钢纤维的分布.由图1 可见，短钢纤维的埋深长度在0～0.5lf-s之间平均分布，短钢纤维的有效埋深长度le-s按式（5）计算.

图1 混凝土单元中短钢纤维的分布Fig.1 Distribution of short steel fibers

为了计算2 种长度钢纤维的桥接作用，假设有限元模型单元的特征长度Lc等于短钢纤维有效埋深长度le-s.如图1 所示，短钢纤维一定会穿过混凝土开裂面，且仅穿过1 个开裂面.因此，混凝土开裂面上短钢纤维的有效根数Nf-s按式（6）计算.

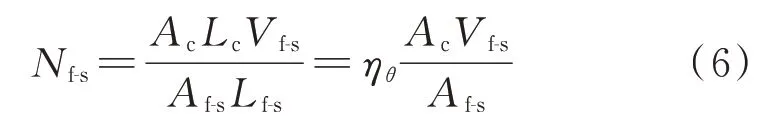
式中：Ac、Af-s分别为混凝土单元和短钢纤维的横截面面积.

图2 给出了混凝土单元中长钢纤维的分布.由图2 可见，长钢纤维在混凝土基体中均匀分布，假设长钢纤维会同时穿过有限元模型中2 个开裂面.长钢纤维的最小埋深长度为0，最大埋深长度为0.5lf-l，长钢纤维的有效埋深长度le-l按式（7）计算；长钢纤维的有效根数Nf-l按式（8）计算.

式中：Af-l为长钢纤维的横截面面积.

3 混杂钢纤维的增强作用

混杂钢纤维在混凝土开裂面上的桥接作用相互独立，利用混凝土开裂面上单根钢纤维轴向应力乘以钢纤维根数，来分别计算2 种钢纤维的增强作用，如式（9）、（10）所示.

式中：σmf-s、σmf-l分别为开裂面上短、长钢纤维的增强应力；σf-s、σf-l分别为单根短、长钢纤维的轴向应力.

3.1 单根钢纤维的增强作用

采用黏结-滑移模型来模拟开裂面上单根钢纤维的桥接作用，计算纤维黏结应力与滑移位移间的关系，其包含纤维部分脱黏阶段（裂缝宽度w不大于钢纤维临界滑移量smax）和完全脱黏阶段（w＞smax）2部分［12-14］，如式（11）中所示.

式中：τf为钢纤维与混凝土基体之间的剪切应力；s为钢纤维滑移量；μ、σN分别为钢纤维与混凝土之间的摩擦系数和握裹应力，基于苏庆田等［15］和Tai 等［16］的试验研究，近似取值为μ=0.6，σN=12.8 MPa；τmax为钢纤维拔出过程中的黏结强度.

由Sezen 等［17］进行的钢纤维拔出试验，τmax近似为基体抗拉强度ffc-tu的2 倍.

对混凝土基体中的钢纤维取为隔离体进行受力分析，如式（13）所示.

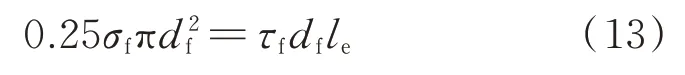
式中：σf为钢纤维的轴向应力；df、le分别为钢纤维的直径和有效埋深长度.

将式（11）、（12）代入式（13）中，建立纤维部分脱黏阶段钢纤维轴向应力σf的计算式.

式中：Ef为钢纤维的弹性模量.

对于钢纤维完全脱黏后的滑移阶段，钢纤维与混凝土基体之间的摩擦作用提供剪应力，用钢纤维接触长度ld代替钢纤维有效埋深长度le，忽略钢纤维在拔出过程中钢纤维和混凝土的受拉变形，ld按式（15）计算.

建立钢纤维完全脱黏阶段（w＞smax）的钢纤维轴向应力计算式如下.

图3 给出了混凝土开裂后混杂钢纤维剪切应力随裂缝宽度的变化，其中smax-l、smax-s分别为长、短钢纤维的临界滑移量.由图3 可见：2 种钢纤维在拔出过程中具有相同的黏结强度；短钢纤维由于具有更短的埋深长度，因而更早到达最大黏结应力.

图3 混杂钢纤维剪切应力随裂缝宽度的变化Fig.3 Variation of shear stress of hybrid fibers with crack width

3.2 开裂面上混杂钢纤维的增强作用

基于混杂钢纤维与混凝土基体间的黏结状态，将混杂钢纤维增强作用分为3 个阶段.

第1 阶段，长、短钢纤维均处于部分拔出阶段，即w≤smax-s，混杂钢纤维增强作用随着裂缝扩展而增强.将式（14）代入式（9）、（10），分别计算开裂面上短、长钢纤维增强应力.

式中：σmf-s、σmf-l分别为HySFRC 中混凝土开裂后短、长钢纤维应力.

第2 阶段，长钢纤维仍处于部分脱黏阶段，短钢纤维完全脱黏、在混凝土孔中整体滑动，即smax-s＜w＜smax-l.将式（14）分别代入式（9）、（10），得到开裂面上短、长钢纤维增强应力.

第3 阶段，长、短钢纤维均完全脱黏、在混凝土孔中滑动，smax-l＜w.将式（14）代入式（9）、（10），可以得到第3 阶段开裂面上短、长钢纤维的增强应力.

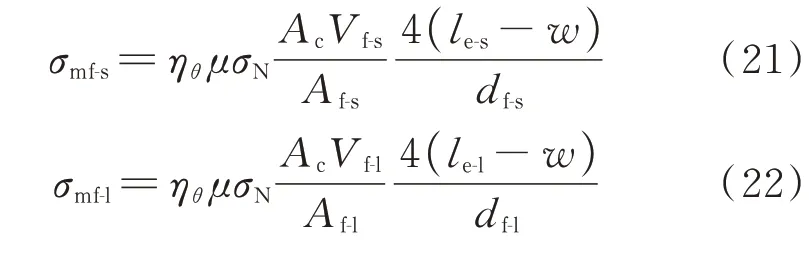
4 混杂钢纤维混凝土的本构模型

混杂钢纤维混凝土HySFRC 在单向受拉状态下的增强应力σfc分别由混凝土基体，短、长钢纤维增强应力组成，如式（23）所示.

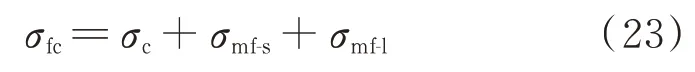
式中：σc为混凝土基体的增强应力.

将式（17）、（18）代入式（23）中，得到HySFRC 轴向应力与裂缝宽度的关系，基于混杂钢纤维增强作用的3 个阶段，在混凝土经典弥散开裂本构模型的基础上，得出了HySFRC 的本构模型.

第1 阶段，HySFRC 的本构模型如下：

第2 阶段，HySFRC 的本构模型如下：

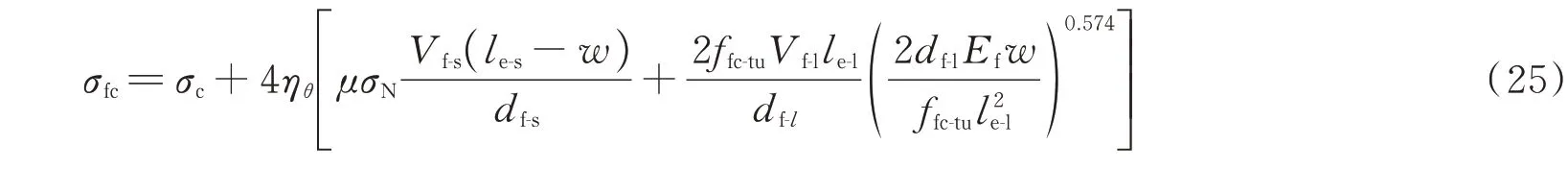
第3 阶段，HySFRC 的本构模型如下：

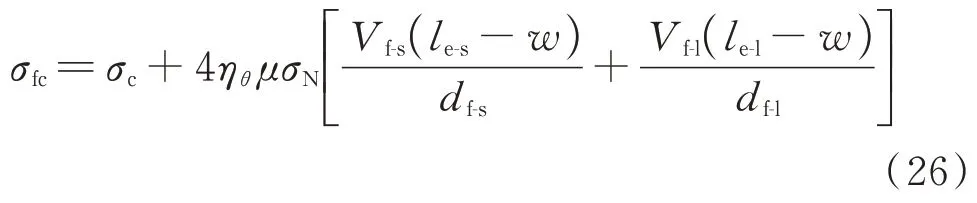
5 本构模型的试验验证及分析

基于Kim 等［18］进行的HySFRC 四点弯曲试验，采用本文所建立的HySFRC 本构模型，在有限元软件Abaqus 中建立相应的有限元模型.试件尺寸为100 mm×100 mm×400 mm，为了消除支座与试件之间应力集中现象的影响，在模型中为钢纤维混凝土试件与支撑、加载板之间分别建立接触，实现试件与支撑、加载板之间的滑动，如图4所示，并在表1 中分别给出混杂钢纤维混凝土试件中长、短钢纤维和混凝土基体的尺寸及力学性能.

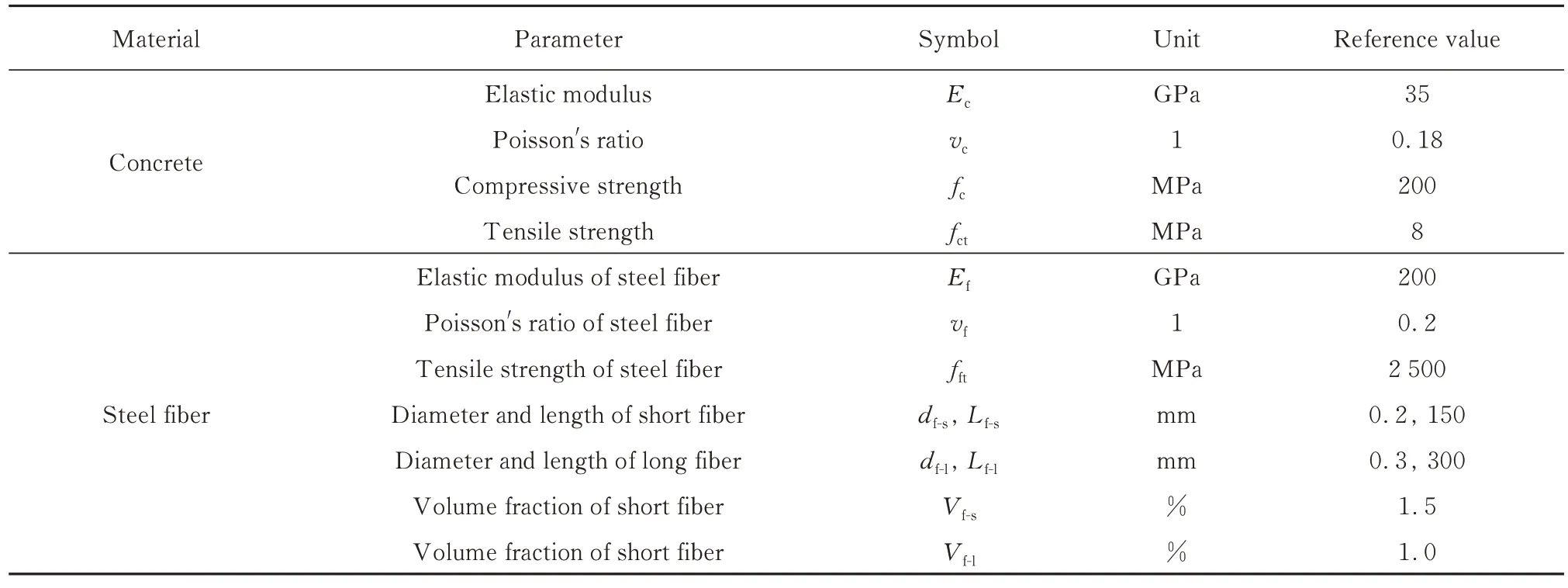
表1 钢纤维和混凝土基体的尺寸及力学性能Table 1 Dimensions and mechanical properties of steel fibers and concrete

图4 四点弯曲试件的尺寸和有限元模型Fig.4 Finite element model of 4-point bending specimen

图5 给出了混杂钢纤维混凝土试件四点弯曲试验的荷载-位移曲线.由图5 可见，混杂钢纤维混凝土试件的数值模拟结果与试验数据整体吻合良好.说明有限元模型有效地预测了混杂钢纤维混凝土试件开裂后的力学响应，试件在开裂后仍表现出良好的承载能力.

图5 混杂钢纤维混凝土试件四点弯曲试验的荷载-位移曲线Fig.5 Load-displacement curve of HySFRC specimen in four-point bending test

图6 显示了四点弯曲试验峰值荷载时刻混杂钢纤维混凝土试件的轴向应力分布.为了清晰显示四点弯曲试验中混杂钢纤维混凝土试件的变形，将有限元模型的变形放大系数均设为20 倍.由图6 可知，混杂钢纤维混凝土试件的压应力始终小于抗压强度，说明受压状态下的混杂钢纤维混凝土处于弹性阶段.

图6 四点弯曲试验峰值荷载时刻混杂钢纤维混凝土试件的轴向应力分布Fig.6 Distribution of axial stress of HySFRC specimen at the peak load in four-point bending test

在混杂钢纤维混凝土试件初次开裂时刻，在纯弯段底部轴向应力达到开裂强度，同时试件其他部分拉应力较小.随着裂缝扩展，混杂钢纤维混凝土试件拉应力最大值的位置从底层开始向上移动，中性轴明显上移.当载荷达到峰值时，纯弯段大部分处于受拉开裂状态.在初裂时刻，试件塑性变形仅发生在弯曲段的底部.当达到峰值载荷时，试件纯弯部分几乎都出现了明显的塑性变形.

6 结论

（1）在混凝土开裂后，混杂钢纤维的桥接作用被激活，利用黏结-滑移模型计算混杂钢纤维对混凝土的增强作用，建立了混杂钢纤维应力与裂缝宽度的关系.由于短钢纤维具有更短的埋深长度，其剪切应力比长钢纤维更早到达黏结强度.考虑混杂钢纤维与混凝土基体之间的脱黏状态，将混杂钢纤维对混凝土的增强作用分为3 个阶段.

（2）对应钢纤维增强作用的3 个阶段，分别建立了混凝土开裂面上混杂钢纤维增强应力与裂缝宽度的关系.基于普通混凝土经典弥散开裂本构模型，考虑开裂面上混杂钢纤维的桥接作用，建立了适用于混杂钢纤维混凝土的本构模型.

（3）将所建混杂钢纤维混凝土本构模型引入有限元软件Abaqus 中，建立混杂钢纤维混凝土四点弯曲试验有限元模型，并进行数值模拟分析.通过比较数值模拟结果与试验数据，充分验证了所提出本构模型的正确性.