多线谱振动噪声主动控制中误差传感器的优化配置
周刘彬, 刘记心, 杨铁军
(1.武汉第二船舶设计研究院,武汉 430205; 2.哈尔滨工程大学 动力与能源工程学院,哈尔滨 150001)
多线谱振动噪声主动控制中误差传感器的优化配置
周刘彬1, 刘记心1, 杨铁军2
(1.武汉第二船舶设计研究院,武汉 430205; 2.哈尔滨工程大学 动力与能源工程学院,哈尔滨 150001)
针对振动主动控制中的误差传感策略问题,改进了现有的传感器优化算法,求解过程采用整数编码和混合编码的遗传算法,在保证整体减振效果基本不变的前提下减少传感器数目并优化其位置,使整个控制系统的规模得到了降低。同时为了消除多通道主动控制时各通道之间的耦合作用,采用FxLMS算法,在浮筏到舱段振动传递途径中安装了4台液压作动器,误差信号同时作为每个作动器的反馈信号,结合提出的误差传感优化策略,对多个激励频率的主动隔振进行了详细的实验研究。实验结果表明,对舱段结构上优选出来的4个误差点进行有效控制后,舱段结构上22个误差点的全局减振效果基本不变,且10个监测用传声器的声压得到了有效的抑制。
误差传感器;优化配置;主动隔振;声辐射;实验研究
在结构振动主动控制中,一方面由于传感器及其配套的数据采集和处理系统成本较高,另一方面使用太多的传感器将导致控制系统变得过于复杂,甚至影响控制系统的性能和稳定性,因此不管采用何种控制策略,都希望尽可能的使用较少的传感器,并对其数量和位置进行优化配置。
要进行传感器的优化配置,首先要确定合适的优化配置准则,即优化的目标函数,目前振动控制中常用的传感器优化准则有可控度/可观度准则[1-2]、系统能量准则[3-4]、系统响应准则[5]、失效和可靠性准则[6]、控制溢出/观测溢出准则[7-8]等,根据不同的控制模型和控制目的选用不同的单一配置准则或者混合使用两种或两种以上的准则。其次传感器的优化配置还需选用适当的优化方法,非线性规划优化法[9-10]、序列法[11-12]和推断算法[13]等是较早常用的解决组合问题的优化方法,但这些优化算法都容易陷入局部最优解,通常得到的只是次优解,后来提出的随机类方法,如模拟退火算法[14]、遗传算法[15-16]、蚁群算法[17]、粒子群算法[18]等,由于该类方法不易陷于局部最优解,在解决组合优化问题中被广泛应用并出现很多成功应用的先例。
刘福强等[19]对2000年之前的这些优化配置准则和方法进行了较为全面详细的回顾总结,近年来国内外在这些配置准则和优化方法上做了大量更进一步的研究。以独立模态最优控制方法为基础,任建亭等[20]采用控制系统作动力消耗能量最小和传感器测量信号能量最大,分别优化设计了悬臂梁控制系统的作动器和传感器的位置;张宪民等[21]利用能够综合反映主动控制器作动和检测能力及避免“溢出”的性能指标函数,采用约束变尺度法,确定了连杆机构中作动器和传感器的最佳布置位置;Kincaid等[22]改进了一种简单静态禁忌搜索算法,使用该算法来进行作动器和传感器位置的D-最优设计,并在一个包含80个节点的桁架结构上进行验证;黄建平[23]为了减小模态滤波器提取模态坐标的误差,采用一种次优方法来优化传感器的位置配置,并以悬臂梁为模型进行了详细研究;Liu等[24]针对二维弹性板,以空间H2范数为基础,采用二进制编码遗传算法寻找传感器和执行器的最优位置;Güney[25]等设计了一个简单的H∞控制器,基于梯度无约束极小化,采用闭环的方式对柔性梁结构中的作动器和传感器的最佳布置位置进行了详细的理论推导和分析;缑新科等[26]基于遗传模拟退火算法,以结构总储能最小为优化目标,对简支梁振动主动控制中传感器和作动器的位置布置进行了优化计算。
以上这些研究多是在不限定传感器个数的情况下寻找最优布置位置,而且针对的模型多为简单的梁、板结构。工程实际中,被控对象的模型往往很复杂,可选择的被控点数量很多,从减小控制经济成本和控制系统规模两方面考虑,必须在优化传感器位置的同时,减少传感器的数目。陆洋等[27]针对直升机结构响应主动振动控制问题,利用整数遗传编码算法,在不减少待减振点数目的前提下,减少传感器数目并优化其位置,并保证系统全局减振效果基本不变,从而有效降低了整个控制系统的控制规模。但他们在利用遗传算法构建目标函数时,把作动器的输出作为目标函数的部分加权值来处理,这样会影响作动器的最优输出力,进而影响整个控制效果。
本文在陆洋等人的研究基础上,改进了目标函数,并采用整数编码和混合编码遗传算法来进行求解,彻底以作动器的真实局部最优控制输出构造全局目标函数,并搭建了相关浮筏试验台架,进行了仿真和试验验证。
1 构建控制目标函数
要进行传感器的位置优化,首先要确定控制目标函数,当有m个传感器、p个作动器时,传感器测得的误差信号可表示为
em=dm+Gmpup
(1)
式中:em是控制后的误差信号,为m×1的向量;dm是控前的响应,为m×1的向量;up为控制力,为p×1的向量;Gmp为控制通道的导纳矩阵,包含m个传感器和p个作动器之间的一一对应传递关系,为m×p的矩阵。
定义控制目标为这m个测点的加速度均方和,则目标函数可表示为
(2)
由最优控制可得最优控制量为
(3)
则目标函数的最小值可表示为
(4)
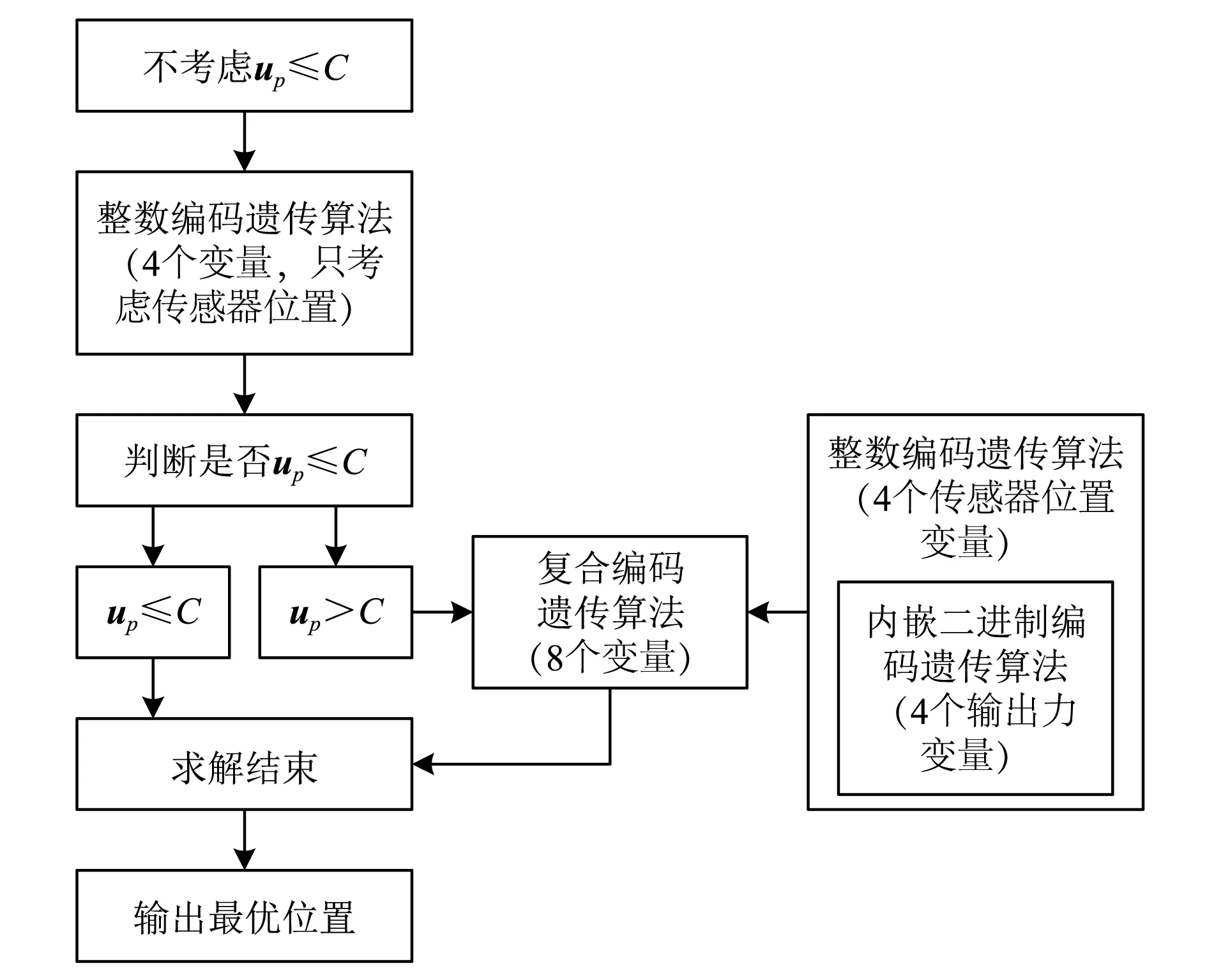
当控制系统有m个传感器和p个作动器时,控制通道的导纳矩阵Gmp为m×p的矩阵,需要占用m×p条控制通道。当m较大传感器数目较多时,控制规模会很大。现考虑在不改变作动器数目和位置、保证控制系统全局控制性能基本不变的前提下,减少传感器数目并优化其位置,使控制系统的控制规模得到降低。现用q个传感器来代替之前的m个传感器(q eq=dq+Gqpp (5) 式中:eq为控制后的误差信号,为q×1的向量;dq为控前的响应,为q×1的向量;p为控制力,为p×1的向量;Gqp为控制通道的导纳矩阵,包含q个传感器和p个作动器之间一一对应的传递关系,为q×p的矩阵。 此时目标函数可表示为 (6) 由最优控制可得最优控制量为: (7) 将局部最优控制力带入全局目标函数式(2),此时目标函数的最小值可表示为 (8) 式中:dm仍为m×1的向量,对应原先各待减振点;而p,opt为减少传感器数目、优化传感器位置以后,用p个作动器控制q个传感器时作动器的最优控制量。即以局部最优控制力构造全局目标函数,使用比原先更少的传感器控制原先各待减振点的振动水平,在降低控制规模的同时尽可能保持原系统的控制效果。 在实际工程中,作动器的输出不可能无限制,往往都有一个最大限制输入,即目标函数需要加一个限定条件,变为 (9) 本文搭建的试验台如图1所示,主要由黄色的框架式浮筏、灰色的弹性舱段、26个空气弹簧及其安装支架、18个BE-400隔振器及其安装支架、4台由电机带动反向旋转的偏心质量对的激振设备(M1~M4)、4台液压执行器组成。 四台液压作动器对称安装在浮筏和舱段结构之间,22个加速度传感器布置在舱段上,作为评价点;4个加速度传感器布置在上述22个传感器其中的4个旁边,作为主动控制时的误差信号;同时在舱段结构四周布置了10个传声器,以监测整个舱段结构的声辐射;除此之外,为评估整个浮筏的振动状况,在浮筏上还布置了另外6个加速度传感器。 (a) 三维模型图 (b) 试验现场图图1 弹性舱段结构上的浮筏主动隔振系统Fig. 1 The picture of the active vibration isolation experimental test-rig 本实验台架安装的四台液压作动器,最大动态输出力3 500 N,考虑到整个控制流程操作的简易性,所有工况的传感器数目都从22个优选到4个,即式(9)中m=22,p=4,q=4,C=3 500。对于上式的求解,这里采用整数编码和混合编码的遗传算法进行求解,求解流程如图2所示。先不考虑输出力up≤C的限制,利用整数编码遗传算法进行求解,此时只考虑传感器位置4个变量,经整数编码计算得到的up与C做比较,满足up≤C则求解结束,输出最优位置。否则,启动混合编码遗传算法进行求解。混合编码遗传算法对传感器位置仍采用整数编码,在求解up时采用二进制编码,以保证up≤C。 图2 遗传算法求解流程Fig. 2 The solving process of genetic algorithm 本节建立试验台的有限元模型,进行相关验证分析。四台激振器在不同转速下产生的激励力作用在浮筏上,控制目标为减小22个待减振点(即舱段结构上18个隔振器安装位置和4个作动器安装位置)的加速度均方和,目标函数为式(9)。初级振源、各作动器与备选传感器位置之间的频响函数由有限元计算求得。 M1~M4四台激振设备旋转频率分别取12 Hz、21 Hz、34 Hz、49 Hz,激励力的幅值依次取1 000 N、1 500 N、800 N、400 N,经遗传算法优化得以下四个最优误差点3、4、11、14。22点加速度均方和,控前1.23 m/s2(121.8 dB);22个误差点全考虑时,目标函数最低可降至0.53 m/s2(114.49 dB);只考虑3、4、11、14四点时,目标函数最低可降至0.77 m/s2(117.73 dB)。 四台作动器在各个频率下的最优输出力如图3所示,图(a)全考虑22个传感器,图(b)只考虑3、4、11、14四点。由图可知,作动器的输出均未超过3 500 N。图4为各待减振点在分别考虑总的22个和4个最优位置传感器时的振动控制水平,由图可知,3、4、11、14四点的加速度响应几乎被削减到零。以4个最优位置传感器作为控制目标时,会引起其余某些误差点的加速度响应略有放大,如34 Hz第16~22个误差评价点。 可见采用该传感器优选方法,的确可以以局部最优控制力构造全局目标函数,能够在保证整体减振效果的前提下减少传感器数目,降低控制系统的规模。 (b)只考虑3、4、11、14四点 (a) 12 Hz (b) 21 Hz (c) 34 Hz (d) 49 Hz 多线谱浮筏主动隔振系统的工作流程图如图5所示,其工作过程可简单归纳如下:首先启动液压作动器,电机调控系统设定四台激振设备的转速,经过D425运动控制系统驱动激振设备工作,布置在舱段结构上的22个加速度传感器采集振动信号,并通过遗传算法计算,求得最优误差传感器的位置,并布置4个加速度传感器至这4个位置。停止激振设备,进行误差通道辨识。再次启动四台激振设备,激振设备的转速信号经调理输入到DSP的A/D通道,作为控制算法所需的参考信号。以1~4号误差传感器测量到的舱段结构的加速度响应作为误差信号。采用多输入多输出的FxLMS算法,计算得到相应的控制器输出,经过高通滤波器、低通滤波器和伺服阀驱动器来驱动四台液压作动器工作,施加控制力于浮筏和舱段结构之间,进而抑制浮筏振动向舱段结构的传递,同时布置在舱段周围的10个传声器记录下来控制前后的声压值。 图5 多频率主动控制实验流程图Fig. 5 The experimental flowchart of the multi-frequency vibration active isolation system M1~M4四台激振设备旋转频率依次为62 Hz、52 Hz、39 Hz、44 Hz,相应的激励力幅值为711 N、794 N、786 N、777 N。经过遗传算法计算,优选出4个误差点:2、16、20、22。并得知目标函数22点加速度均方和,控前0.649 4 m/s2(116.25 dB);全考虑22个误差点时,目标函数最低可降至0.182 6 m/s2(105.23 dB);只考虑2、16、20、22四点时,目标函数最低可降至0.221 5 m/s2(106.91 dB)。 (a) 浮筏 (b) 舱段 (c) 传声器图 6 实验结果Fig. 6 The experimental results 图6为该工况的控制效果图,其中图(a)为0~200 Hz浮筏结构上6个传感器的加速度均方和,图(b)为0~200 Hz舱段结构上22个传感器的加速度均方和,图(c)为0~200 Hz舱段结构周围布置的10个传声器的声压均方和。由图(a)知,控前控后浮筏加速度均方和变化不大;图(b)中,39 Hz、44 Hz、52 Hz、62 Hz四个激励频率处的加速度均方和依次降低了17.14 dB、8.54 dB、9.8 dB、7.82 dB,可见主动隔振有效地减小了浮筏到舱段的振动传递;图(c)中,33 Hz、38.5 Hz、40 Hz、42.5 Hz四个激励频率处的声压均方和依次降低了14.04 dB、9.26 dB、13.84 dB、6.09 dB,可知主动隔振在控制振动的同时也较好地控制了空气辐射噪声。 (a) 39 Hz (b) 44 Hz (c) 52 Hz (d) 62 Hz图 7 22个误差点加速度响应Fig. 7 The acceleration responses of 22 error-points 图7为22个待减振点在激励频率处控前控后加速度振动水平,由图中可以看出该工况下几乎所有测点的各个频率成分都得到了较好的控制,整体加速度均方和为0.23 m/s2(107.22 dB),与前面传感器优化仿真计算的106.91 dB很接近。 图8为10个监测用传声器在激励频率处的控前控后声压值,由图中可以看出除了1号测点62 Hz频率成分略有升高,其余测点的各个频率成分均得到了很好的控制效果。本试验台所采用的电机空气噪声很小,且主动隔振对电机的工作状态几乎没有影响,浮筏为框架式结构,对空气噪声影响很小,故可知主要噪声源来自弹性舱段结构,当舱段振动减小,对外的辐射噪声随之减小。 (a) 39 Hz (b) 44 Hz (c) 52 Hz (d) 62 Hz图 8 10个传声器声压值Fig. 8 The sound pressure of 10 microphones 图9为6个浮筏监测点控前控后加速度振动水平,由图中可以看出施加控制后,2、3、6三个测点52 Hz频率成分略有升高,这是由于这三个测点靠近激励设备M2(工作频率52 Hz),设备M2的激励力相对于其他三台设备幅值又最大,总的来看,作动器的输入力对浮筏的影响不大。 (a) 39 Hz (b) 44 Hz (c) 52 Hz (d) 62 Hz图 9 浮筏振动情况Fig. 9 The vibration of floating raft 本文针对结构响应振动主动控制问题,改进了一种已有的传感器优选方法,该方法以局部最优控制电压构造全局目标函数,能够在不减少待减振点数目的前提下,减少传感器数目并优化其位置,使整个系统的控制规模得到降低,且保证系统全局减振效果基本不变,优化过程采用整数编码和混合编码遗传算法进行求解。同时开展了主动控制实验研究,为了消除多通道主动控制时,各个控制通道间耦合作用的影响,实验时考虑各个通道之间的耦合作用,四个误差信号同时作为每个作动器的反馈信号,基于FxLMS 的主动控制算法对该系统进行多通道自适应主动控制。主动隔振的研究结果表明,通过主动隔振对舱段结构上优选出来的4个误差点进行有效控制后,22个误差点的全局减振效果基本不变,且10个监测用传声器的声压得到了有效的抑制。 实验验证了利用该优选方法,能够得到限定传感器数目的最优位置分布,且全局减振效果降低的有限传感器最优布置方案。 [1] LIU Z S, WANG D J, HU H C. Measures of modal controllability and observability in vibration control of flexible structures [J]. Journal of Guidance, Control, and Dynamics, 1994,17(6):1377-1380. [2] XING G Q, BAINUM P M. Actuator placement using degree of controllability for discrete-time systems [J]. Journal of Guidance, Control, and Dynamics, 1993,114:508-516. [3] 李俊宝,刘华,张令弥.自适应拓架结构振动控制中主动构件的最优配置[J].航空学报,1996,17(5):755-759. LI Junbao, LIU Hua, ZHANG Lingmi. Optimal placement of avtive members in active vibration control of adaptive truss structuress [J]. Acta Aeronautica et Astronatutica Sinica, 1996, 17(5):755-759. [4] CHEN G S, BRUNO R J, SALAMA M. Optimal placement of active/passive members in truss structures using simulated annealing [J]. AIAA Journal, 1991, 29(8):1327-1334. [5] SUNAR M, RAO S S. Thermo piezoelectric control design and actuator plaeement [J]. AIAA Journal, 1997,35(2):534-539. [6] MATUNAGA S, ONODA J. Actuator placement with failure consideration for static shape control of truss structures [J]. AIAA Journal, 1995,33(6): 1161-1163. [7] JALIHAL P J, UTKU S, WADA B K. Actuator placement in prestressed adaptive trusses for vibration control [C]∥Proeeedings of SDM Conference. AIAA-93-1694-cP.1993: 3312-3318. [8] RYOU J K, PARK K Y, KIM S J. Electrode pattern design of piezoelectric sensors and actuators using genetie algorithms [J]. AIAA Journal, 1998, 36(2):227-233. [9] SEPULVEDA A E, JIN I M, SCHMIT J L. Optimal placement of active elements in control augmented structural synthesis [J]. AIAA Journal, 1993, 31(10): 1906-1915. [10] SUNAR M, RAO S S. Thermo piezoelectric control design and actuator placement [J]. AIAA Journal, 1997, 35(2):534 -539. [11] TOLSON R H , HUANG J K. Integrated control of thermally distorted large space antennas [J]. Journal of Guidance Control and Dynamics, 1992,15(3): 605-614. [12] 刘福强,张令弥.作动器与传感器优化配置的逐步消减法[J]. 宇航学报,2000, 21(3): 64-69. LIU Fuqiang, ZHANG Lingmi. Successive method for optimal placement of actuators and sensors [J]. Journal of Astronautics, 2000, 21(3):64-69. [13] HAFLCTA R T, ADELMAN H M. Selection of actuator locations for static shape control of large space structures by heuristic integer programming [J]. Computers and Structures, 1985, 20(3): 575-582. [14] KIRKPATRICK S, GELATT C, VECCHI M. Optimization by simulated annealing [J]. Science, 1983,220:671-680. [15] 刘福强,张令弥.遗传算法在主动构件优化配置中的应用[J].振动与冲击,1999, 18(4):16-21. LIU Fuqiang, ZHANG Lingmi. Optmal placement of active members via genetic algorithm [J]. Journal of Vibration and Shock, 1999, 18(4):16-21. [16] LI Q S, LIU D K, TANG J, et al. Combinatorial optimal design of number and positions of actuators in actively controlled structures using genetic algorithms [J]. Journal of Sound and Vibration, 2004,270: 611-624. [17] COLORNIA A, DORIGO M, MANIEZZO V. An investigation of Some Properties of an Ant Algorithm [C]∥ Proceeding of the Parallel Problem Solving from Nature Conference. Brussels: Elsevier Publishing, 1992:509 -520. [18] KENNEDY J, EBERHART R C. Particle swarm optimization [C]∥ Proceeding of IEEE International Conference on Neural Networks. Perth, WA, 1995:1942-1948. [19] 刘福强,张令弥.作动器/传感器优化配置的研究进展[J].力学进展, 2000, 30(4): 506-516. LIU Fuqiang, ZHANG Lingmi. Advances in optimal placement of actuators and sensors [J]. Advances in Mechanics, 2000, 30(4): 506-516. [20] 任建亭,闫云聚,姜节胜.振动控制传感器/作动器的数目和位置优化设计[J].振动工程学报,2001,14(2):237-241. REN Jianting, YAN Yunju, JIANG Jiesheng. Optimal design method for sensors/actuators placement and numbers in the vibration control of flexible structure system [J]. Journal of Vibration Engineering, 2001,14(2):237-241. [21] 张宪民,邵长健,沈允文.弹性连杆机构振动主动控制中作动器与传感器的位置优化[J].振动工程学报, 2001, 14(2): 211-214. ZHANG Xianmin, SHAO Changjian, SHEN Yunwen. Optimal placement of sensors and actuators for vibration control of elastic linkage mechanisms [J]. Journal of Vibration Engineering, 2001, 14(2):211-214. [22] KINCAID R K, PADULA S L.D-optimal designs for sensor and actuator locations [J]. Computers & Operations Research, 2002, 29:701-713. [23] 黄建平.梁结构振动复合主动控制方法研究[D]. 南京:南京航空航天大学,2005:15-45. [24] LIU W, HOU Z K, DEMETRIOU M A. A computational scheme for the optimal sensor/actuator placement of flexible structures using spatial H2 measures [J]. Mechanical Systems and Signal Processing, 2006,20:881-895. [26] 缑新科,崔明月.遗传模拟退火算法在传感器/作动器位置优化问题中的应用[J].自动控制与监测,2008(11):39-41. HOU Xinke, CUI Mingyue. Application of genetic and simulated annealing algorithms in placement optimization of sensor/actuator [J]. Journal of Automatic Control and Monitoring, 2008(11):39-41. [27] 陆洋,顾仲权,凌爱民.直升机结构响应主动控制中传感器优选问题研究[J].振动与冲击,2011,30(6):58-61. LU Yang, GU Zhongquan, LING Aimin. Optimization selection of sensors in active control of structural response for helicopter [J]. Journal of Vibration and Shock, 2011, 30(6): 58-61. Optimal allocation of error sensors in the multi-curve spectrumactive vibration and sound control ZHOU Liubin1, LIU Jixin1, YANG Tiejun2 (1.Wuhan the Second Research Institute of Ships, Wuhan 430205, China2.College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China) Aiming at the optimization of sensors’ number and locations in the active control of structural response, an existing optimization selection method was improved. The method can effectively reduce the number of sensors and find their relevant optimization locations, at the same time the effect of vibration reduction maintains almost the same as before, and the scale of control hardware can be reduced distinctly. The optimization procedure was resolved with the genetic algorithm. In order to eliminate the coupling effects among multi-channel in active control, the FxLMS algorithm was used. Four hydraulic actuators were placed between the floating raft and the hull structure. The error signals were used as feedback signals for each actuator simultaneously, and the improved integer coding genetic algorithm was applied. The effect of active vibration isolation at multiple excitation frequencies was studied experimentally. The experimental results show that the vibration reduction effect of 4 error signals maintains almost the same as that of 22 error signals. The sound pressure of the 10 monitoring microphones is effectively suppressed. error sensors; optimal allocation; active vibration isolation; sound radiations; experimental investigation 国家自然科学基金(51375103;51409199) 2015-10-20 修改稿收到日期: 2016-03-25 周刘彬 男,博士生,1985年1月生 杨铁军 男,博士,教授,1972年10月生 TK05 A 10.13465/j.cnki.jvs.2017.10.028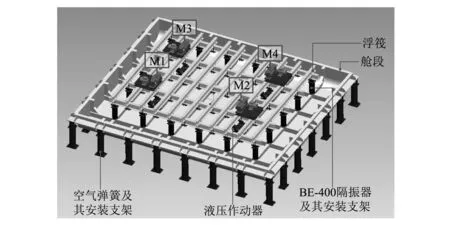

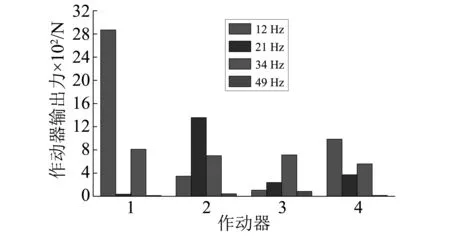
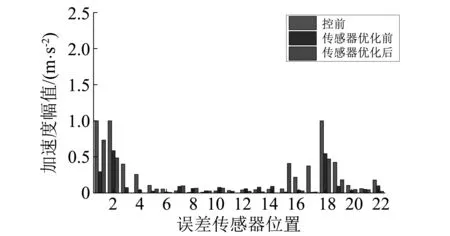
2 传感器优化仿真分析
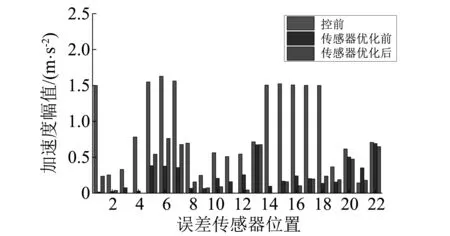
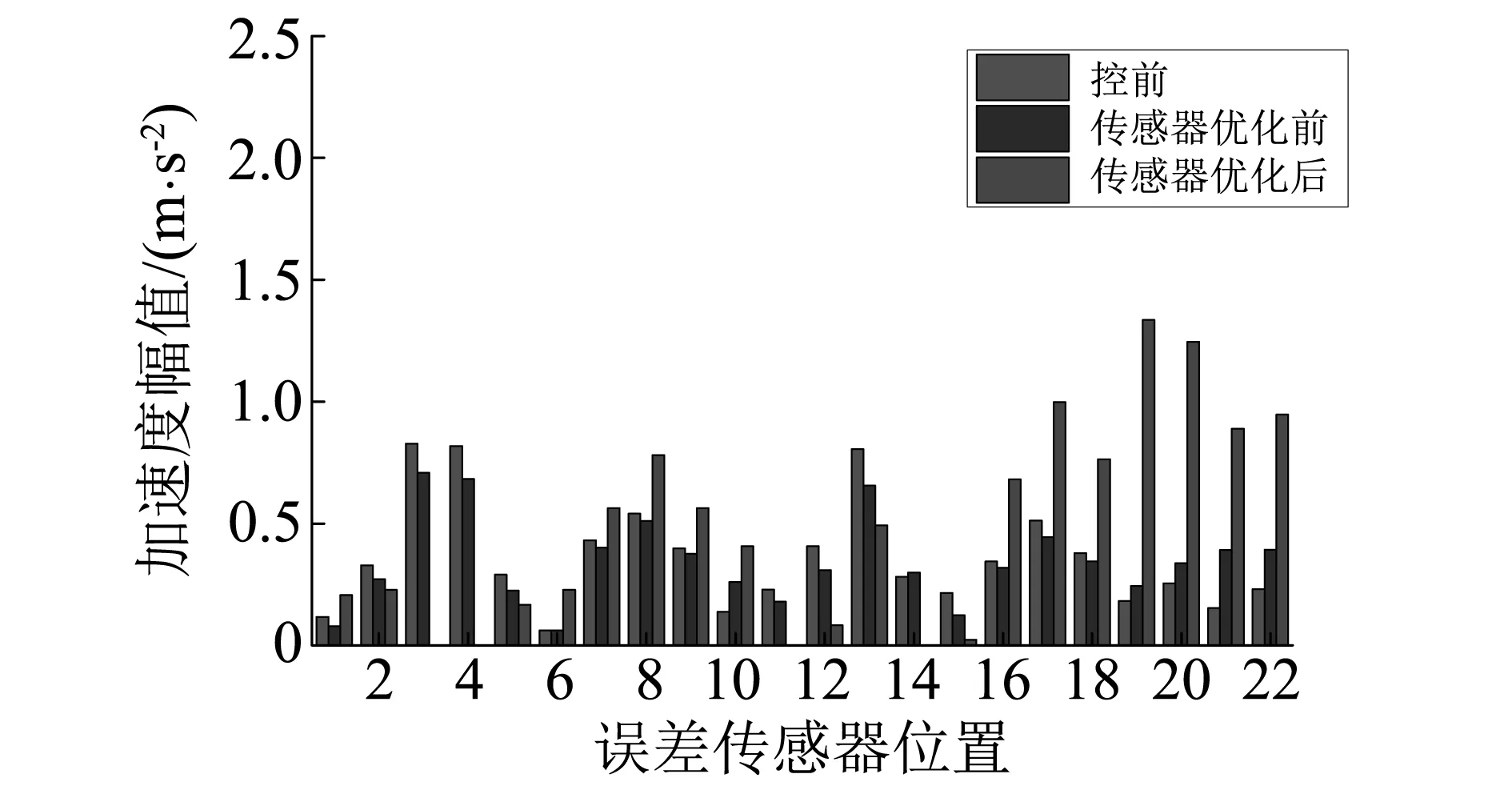
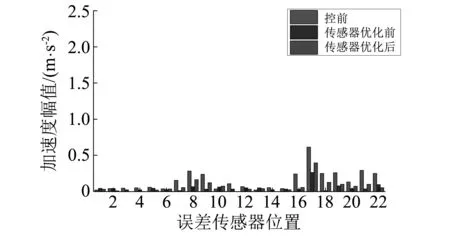
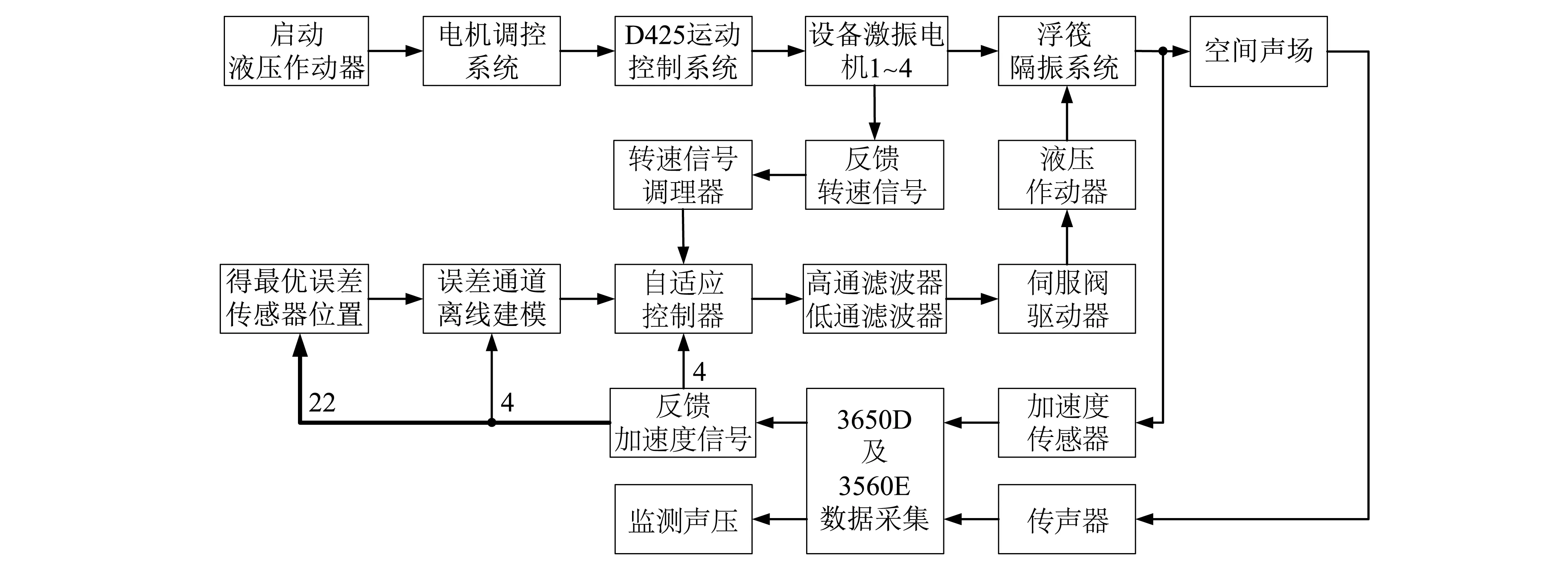
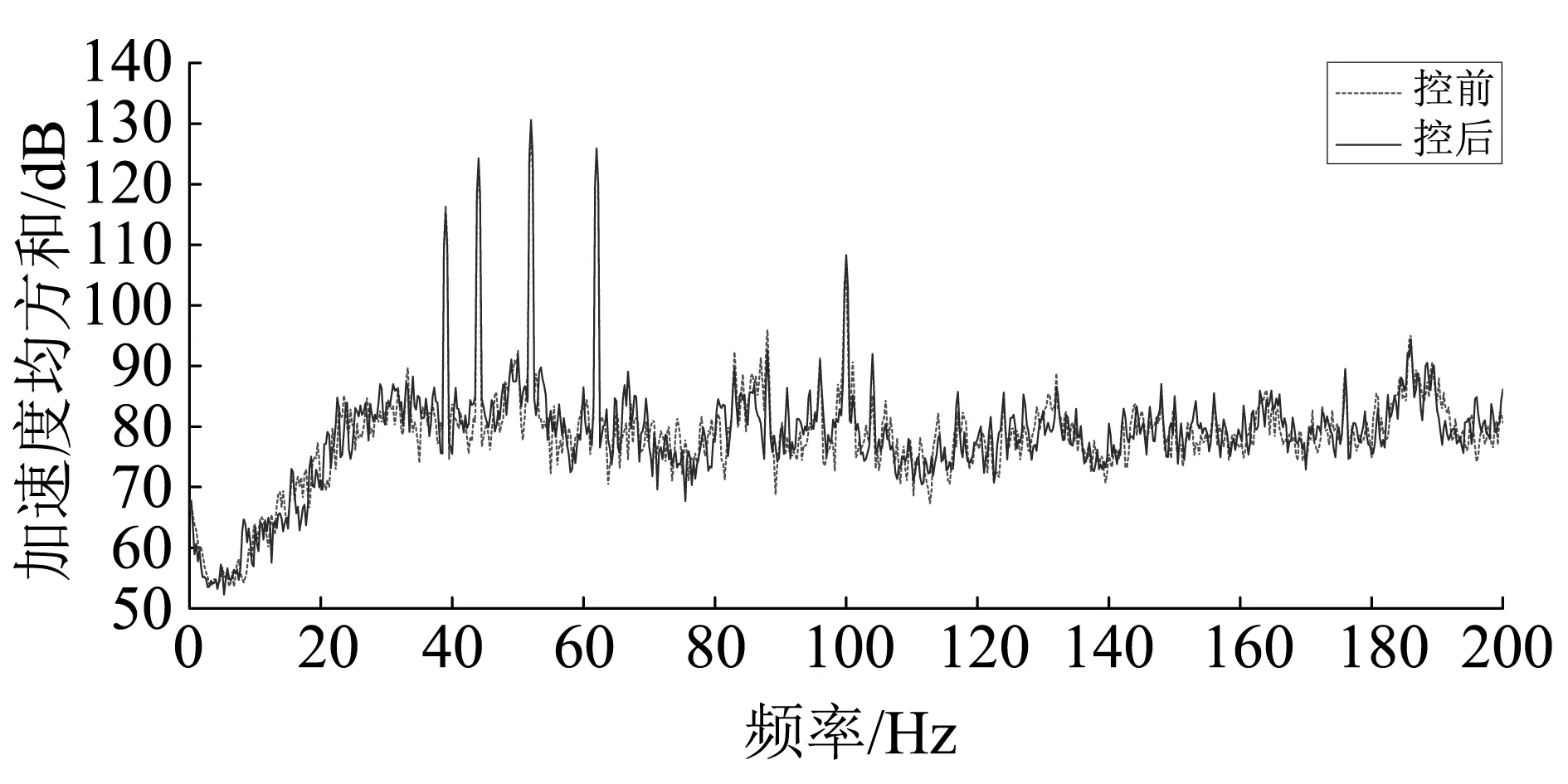
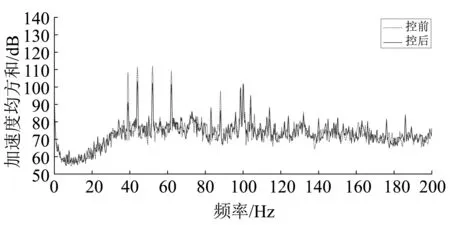
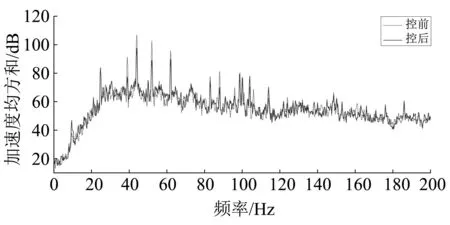
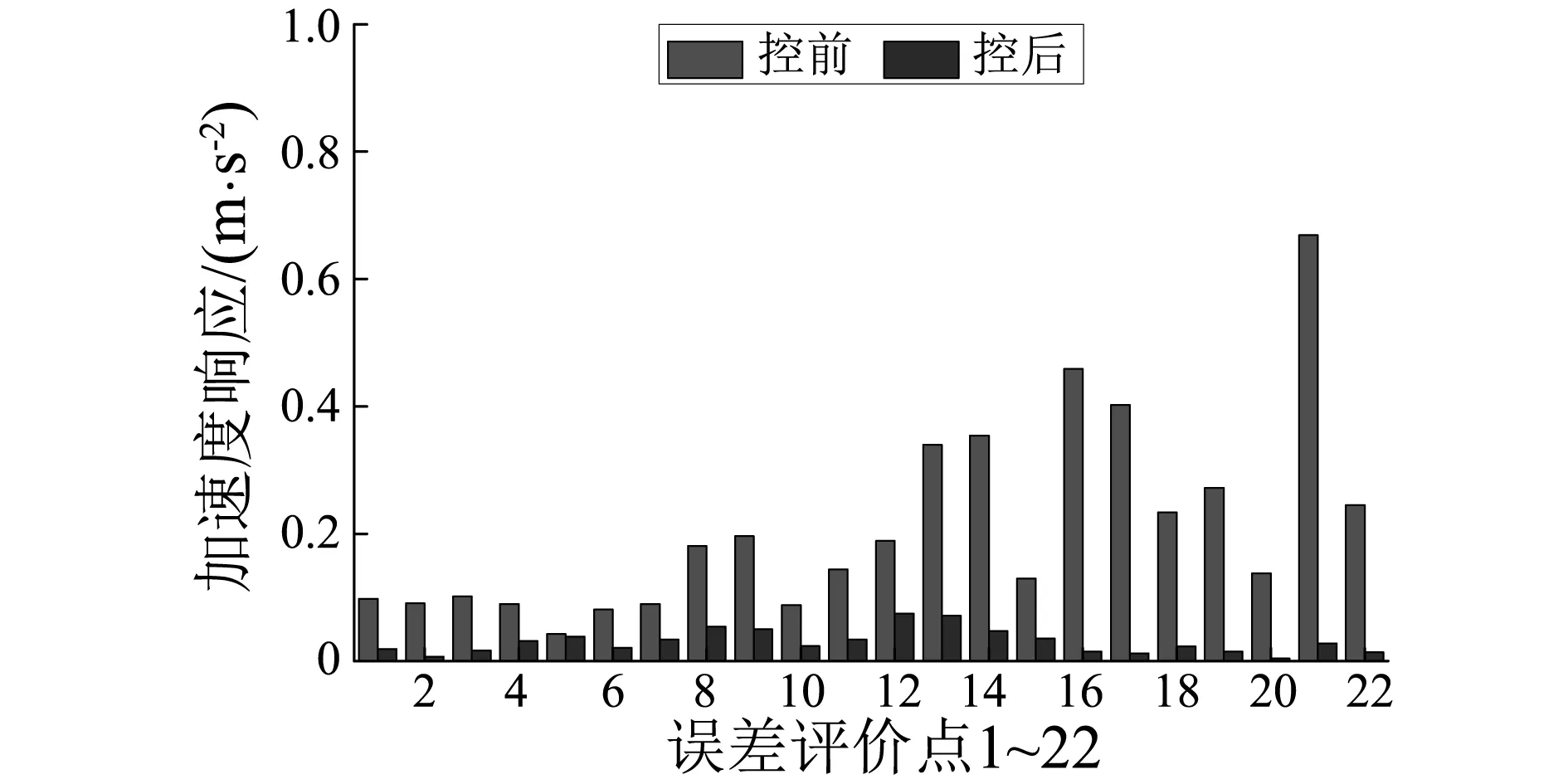
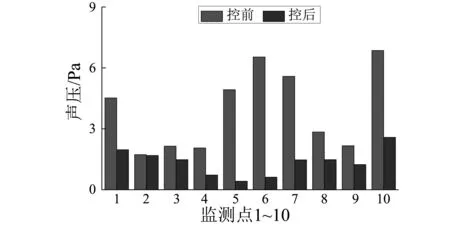
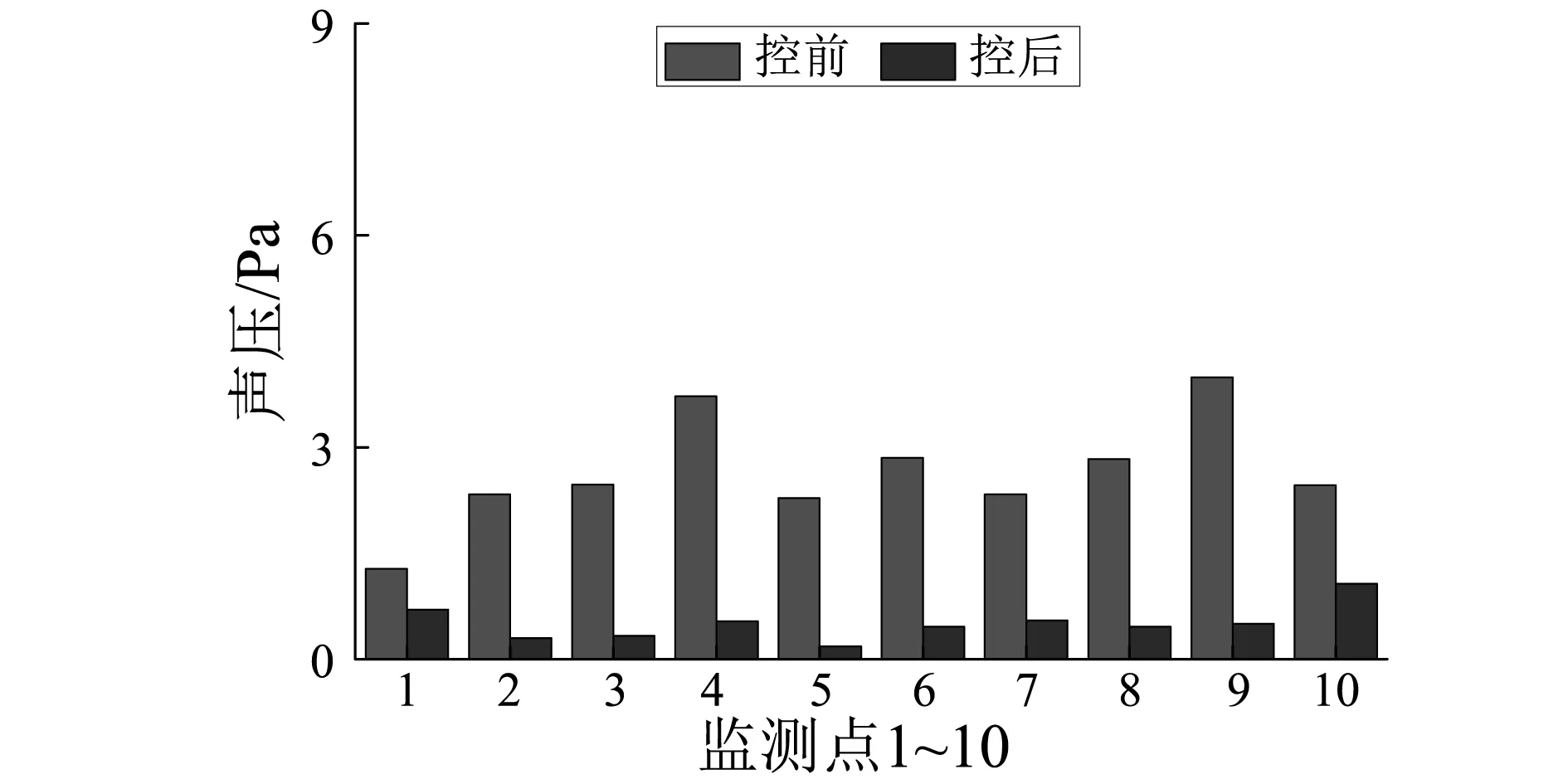
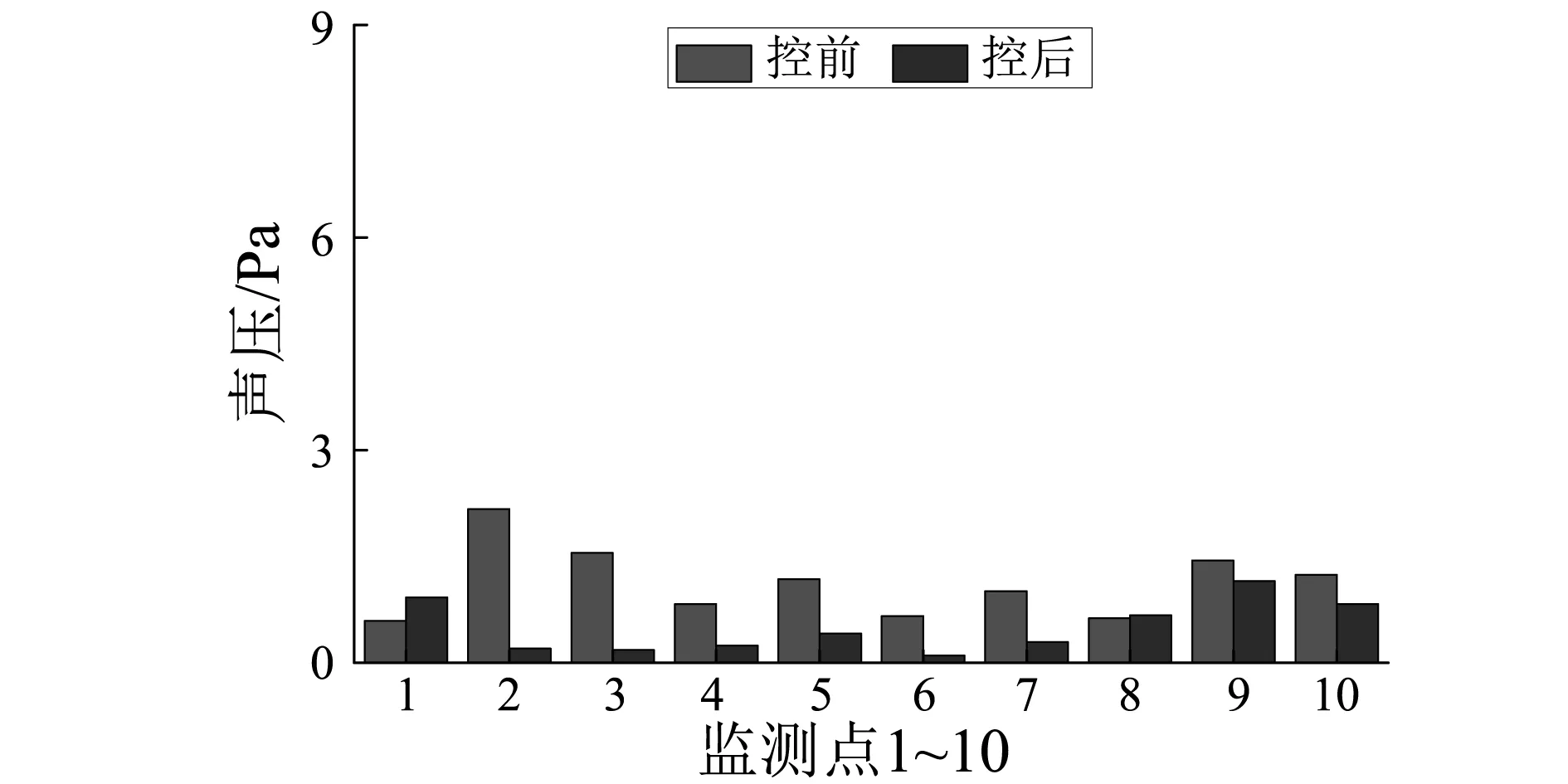
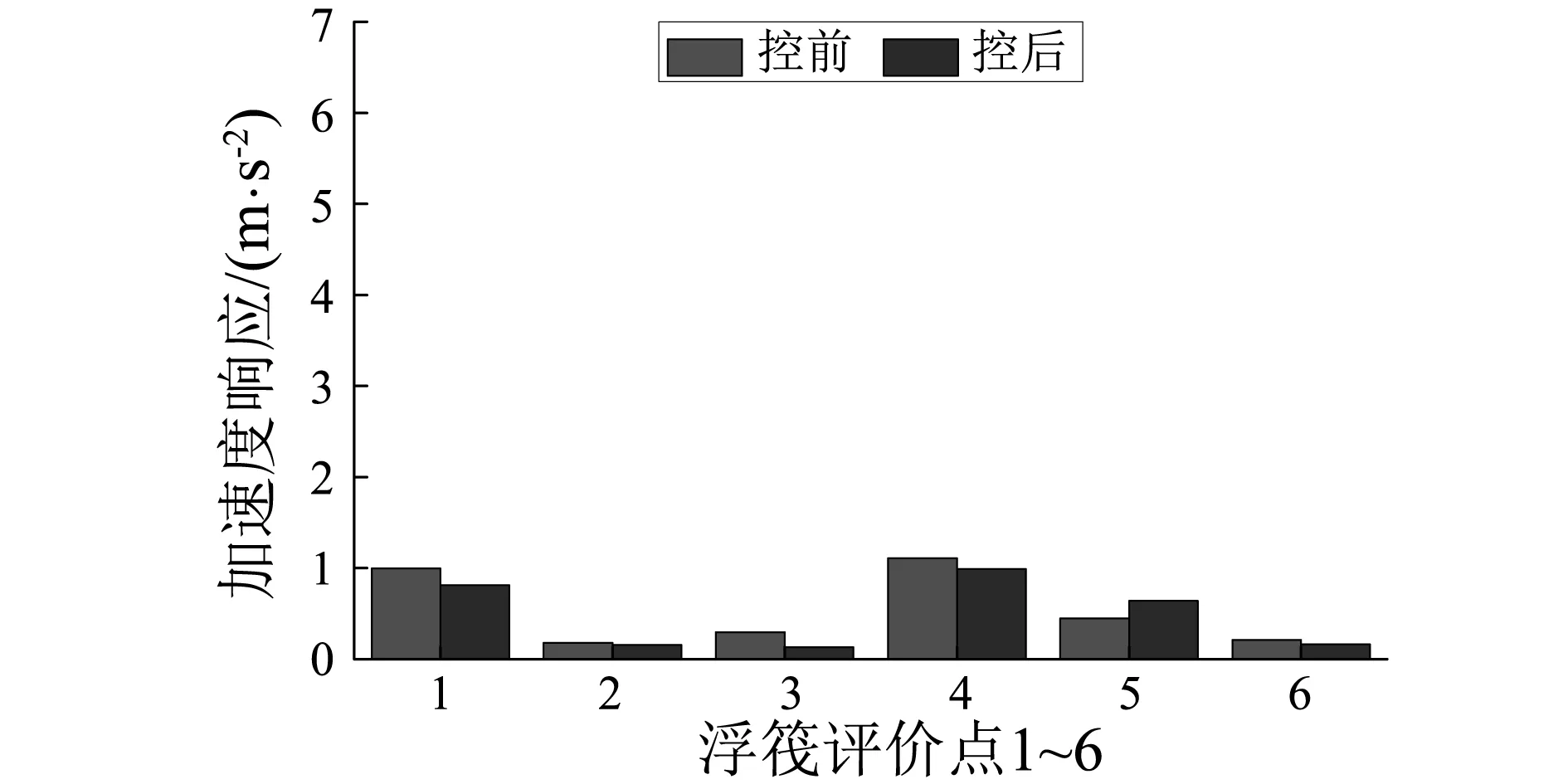
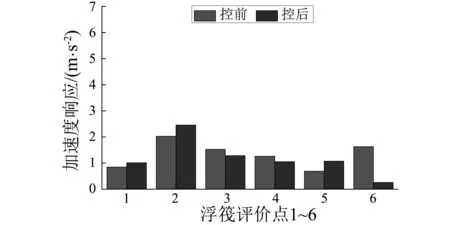
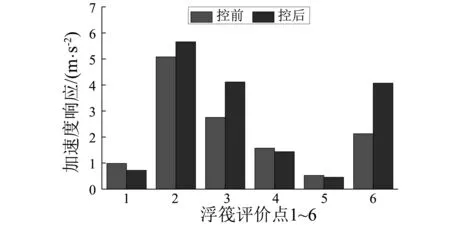
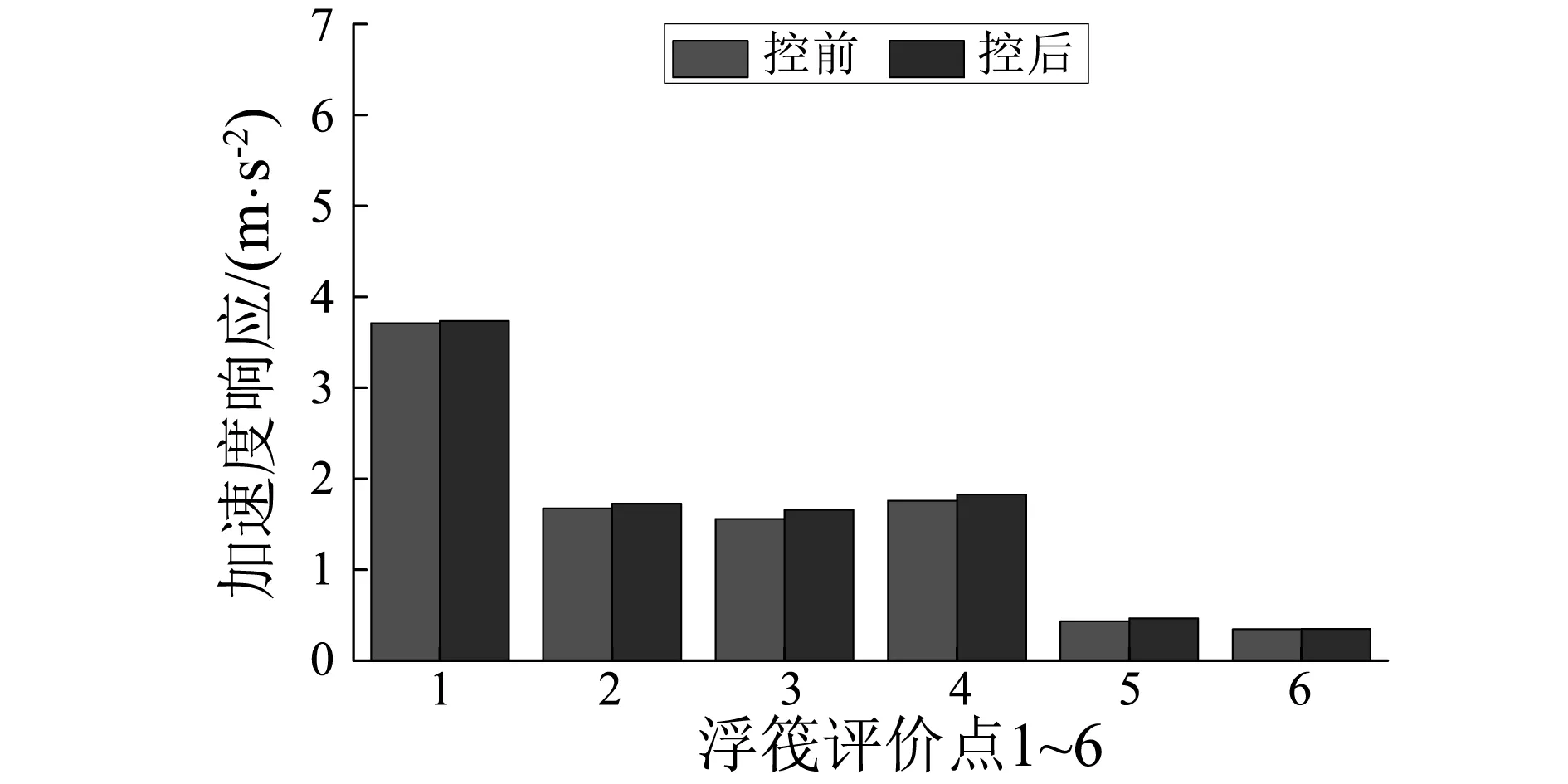
3 多线谱的主动控制实验
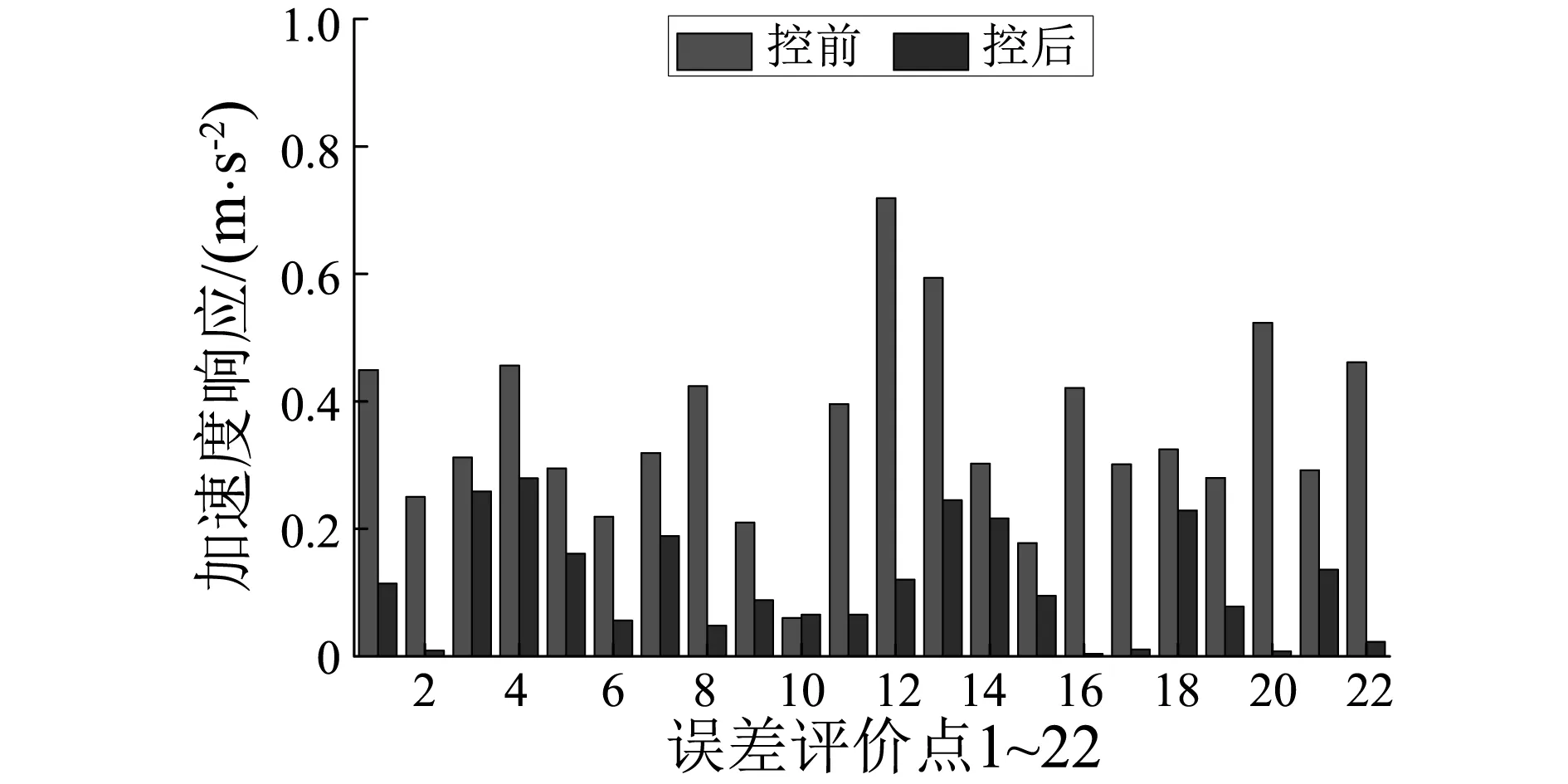
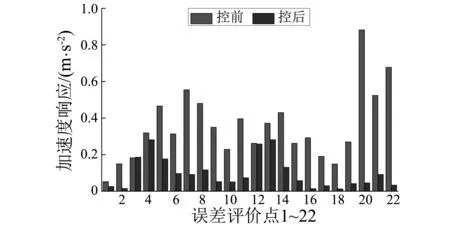
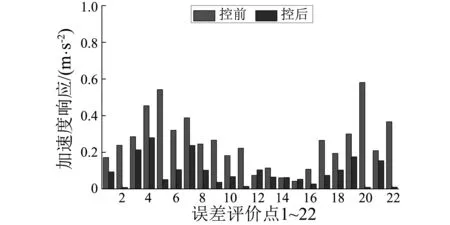
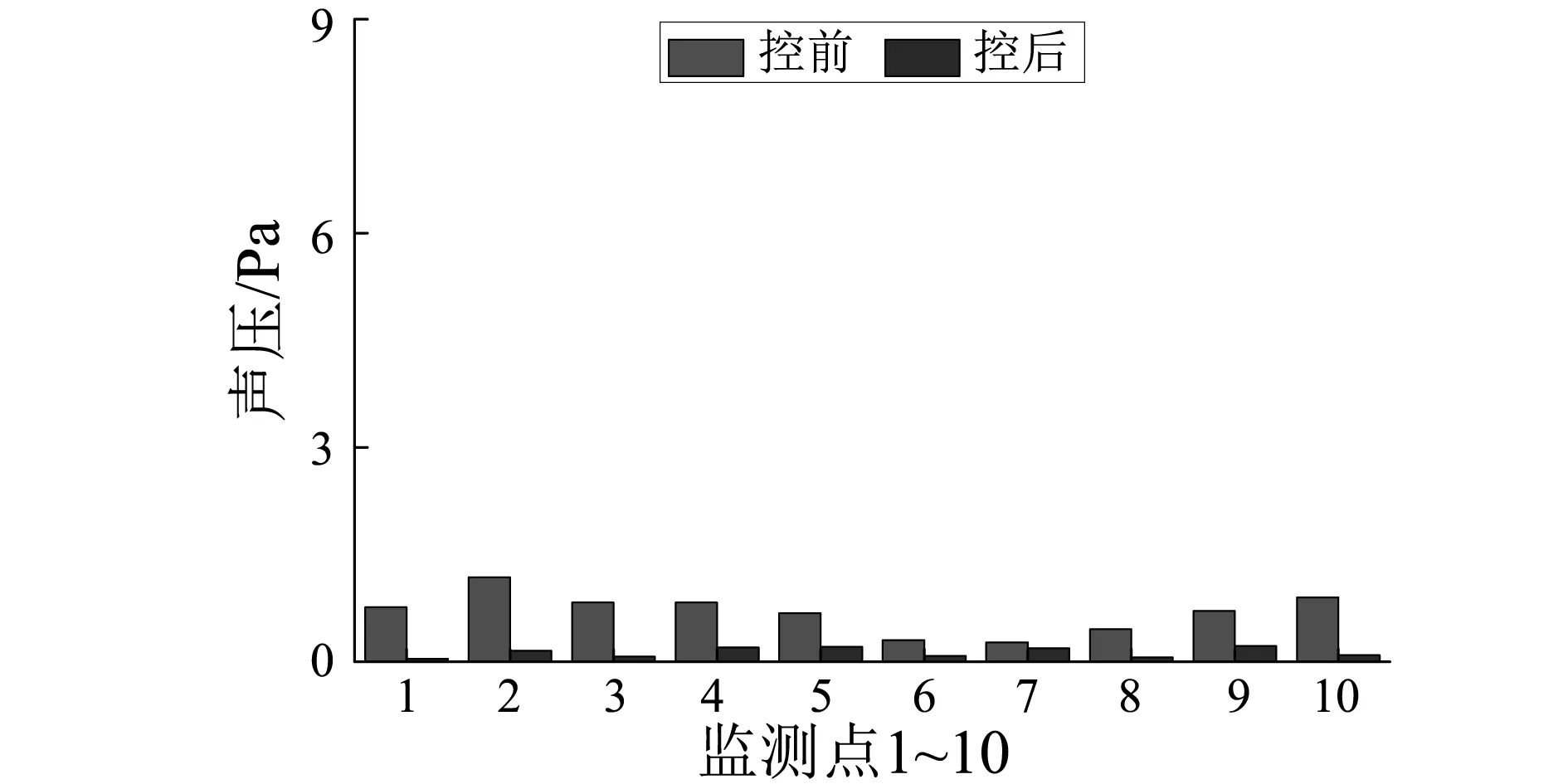
4 结 论


